La trigonométrie est une branche importante des mathématiques qui traite de la relation entre les angles et les longueurs des côtés d'un triangle rectangle. Les six rapports ou fonctions trigonométriques sont le sinus, le cosinus, la tangente, la cosécante et la sécante, et un rapport trigonométrique est un rapport entre les côtés d'un triangle rectangle. Les fonctions sinus, cosinus et tangente sont trois fonctions trigonométriques importantes puisque les trois autres, c'est-à-dire les fonctions cosécantes, sécantes et cotangentes, sont respectivement les fonctions réciproques des fonctions sinus, cosinus et tangente.
- sin θ = Côté opposé/hypoténuse
- cos θ = Adjacent side/Hypotenuse
- tan θ = Côté opposé/Côté adjacent
- cosec θ = Hypotenuse/Opposite side
- sec θ = Hypotenuse/Adjacent side
- lit bébé θ = Côté adjacent/Côté opposé
La fonction tangente est l'une des 6 fonctions trigonométriques utilisées dans formules de trigonométrie .
Table des matières
Formule tangente
La tangente d'un angle dans un triangle rectangle est le rapport de la longueur du côté opposé à la longueur du côté adjacent à l'angle donné. Nous écrivons une fonction tangente sous la forme tan. Considérons un triangle rectangle XYZ et l'un de ses angles aigus est θ. Un côté opposé est le côté opposé à l’angle θ et le côté adjacent est le côté adjacent à l’angle θ.
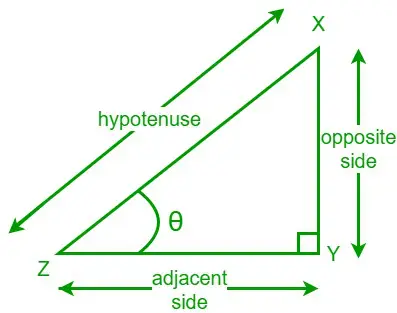
Maintenant, la formule de la tangente pour l’angle θ donné est :
tan θ = Côté opposé/Côté adjacent
Quelques formules tangentielles de base
Fonction tangente dans les quadrants
La fonction tangente est positive dans les premier et troisième quadrants et négative dans les deuxième et quatrième quadrants.
- bronzage (2π + θ) = bronzage θ (1Stquadrant)
- tan (π – θ) = – tan θ (2sdquadrant)
- bronzage (π + θ) = bronzage θ (3rdquadrant)
- tan (2π – θ) = – tan θ (4èmequadrant)
Fonction tangente comme fonction négative
La fonction tangente est une fonction négative puisque la tangente d’un angle négatif est la négative d’un angle tangent positif.
bronzage (-θ) = – bronzage θ
Fonction tangente en termes de fonction sinus et cosinus
La fonction tangente en termes de fonctions sinus et cosinus peut s'écrire comme suit :
tan θ = péché θ/cos θ
Nous savons que tan θ = Côté opposé/Côté adjacent
Maintenant, divisez le numérateur et le dénominateur par l'hypoténuse
tan θ = (Opposite side/Hypotenuse)/(Adjacent side/Hypotenuse)
Nous savons que sin θ = côté opposé/hypoténuse
cos θ = adjacent side/hypotenuse
Par conséquent, tan θ = sin θ/cos θ
Fonction tangente en termes de fonction sinus
La fonction tangente en termes de fonction sinus peut s'écrire comme suit :
tan θ = péché θ/(√1 – péché 2 je)
Nous savons que,
tan θ = péché θ/cos θ
combien de villes aux États-Unis
Des identités pythagoriciennes, nous avons,
sans2θ + cos2θ = 1
parce que2θ = 1 – péché2je
cos θ = √(1 – péché2je)
Par conséquent, tan θ = sin θ/(√1 – sin2je)
Fonction tangente en termes de fonction cosinus
La fonction tangente en termes de fonction cosinus peut s'écrire comme suit :
tan θ = (√1 -cos 2 je)/parce que je
Nous savons que,
tan θ = péché θ/cos θ
Des identités pythagoriciennes, nous avons,
sans2θ + cos2θ = 1
sans2θ = 1 – cos2je
péché θ = √(1 – cos2je)
Par conséquent, tan θ = (√1 – cos2je)/parce que je
Fonction tangente en termes de fonction cotangente
La fonction tangente en termes de fonction cotangente peut s'écrire comme suit :
bronzage θ = 1/lit bébé θ
ou
bronzage θ = lit bébé (90° – θ) (ou) lit bébé (π/2 – θ)
Fonction tangente en termes de fonction cosécante
La fonction tangente en termes de fonction cosécante peut s'écrire comme suit :
tan θ = 1/√(cosec 2 je – 1)
Des identités pythagoriciennes, nous avons,
cosec2θ – lit bébé2θ = 1
lit bébé2θ = cosec2je – 1
cot θ = √(cosec2je – 1)
Nous savons que,
bronzage θ = 1/lit bébé θ
Par conséquent, tan θ = 1/√(cosec2je – 1)
Fonction tangente en termes de fonction sécante
La fonction tangente en termes de fonction sécante peut s'écrire comme suit :
tan θ = √sec 2 je – 1
Des identités pythagoriciennes, nous avons,
seconde2θ – donc2θ = 1
bronzage θ = sec2je – 1
Par conséquent, tan θ = √(sec2je – 1)
Fonction tangente en termes de double angle
La fonction tangente pour un angle double est,
bronzage 2θ = (2 bronzage θ)/(1 – bronzage 2 je)
Fonction tangente en termes de triple angle
La fonction tangente pour un triple angle est,
bronzage 3θ = (3 bronzage θ – bronzage 3 θ) / (1 – 3 bronzage 2 je)
Fonction tangente en termes de demi-angle
La fonction tangente pour un demi-angle est,
tan (θ/2) = ± √[ (1 – cos θ) / (1 + cos θ) ]
tan (θ/2) = (1 – cos θ) / ( sin θ)
Fonction tangente en termes d'addition et de soustraction de deux angles
Les formules de somme et de différence pour une fonction tangente sont :
bronzage (A + B) = (bronzage A + bronzage B)/(1 – bronzage A bronzage B)
bronzage (A – B) = (bronzage A – bronzage B)/(1 + bronzage A bronzage B)
Tableau des rapports trigonométriques
| Angle (en degrés) | Angle (en radians) | péché je | cos θ | tan θ = péché θ/cos θ | cosec θ | seconde θ | lit bébé je |
|---|---|---|---|---|---|---|---|
| 0° | 0 | 0 | 1 | 0/1 = 0 | Indéfini | 1 | Indéfini |
| 30° | p/6 | 1/2 | √3/2 | (1/2)/(√3/2) = 1/√3 | 2 | 23 | √3 |
| 45° | p/4 | 1/√2 | 1/√2 | (1/√2)/(1/√2) = 1 | √2 | √2 | 1 |
| 60° | p/3 | √3/2 | 1/2 | (√3/2)/(1/2) = √3 qu'est-ce que le clustering | 23 | 2 | 1/√3 |
| 90° | p/2 | 1 | 0 | 1/0 = non défini | 1 | Indéfini | 0 |
| 120° | 2p/3 | √3/2 | -1/2 | (√3/2)/(-1/2) = -√3 | 23 | -2 | -1/√3 |
| 150° | 5p/6 | 1/2 | -(√3/2) | (1/2)/(-√3/2) = -1/√3 | 2 | -(23) | -√3 |
| 180° | Pi | 0 | -1 | 0/(-1) = 0 | Indéfini | -1 | Indéfini |
Exemple résolu sur les formules tangentes
Exemple 1 : Trouvez la valeur de tan θ si sin θ = 2/5 et θ est le premier angle du quadrant.
Solution:
Donné,
- péché θ = 2/5
Des identités pythagoriciennes que nous avons,
sans2θ + cos2θ = 1
parce que2θ = 1 – péché2θ = 1 – (2/5)2
parce que2θ = 1 – (4/5) = 21/25
cos θ = ±√21/5
Puisque θ est le premier angle du quadrant, cos θ est positif.
cos θ = √21/5
Nous savons que,
tan θ = péché θ/cos θ
= (2/5)/(√21/5) = 2/√21
bronzage θ = 2√21 /21
Ainsi, la valeur de tan θ lorsque sin θ = 2/5 et θ est dans le premier quadrant est (2√21) /(21)
Exemple 2 : Trouvez la valeur de tan x si sec x = 13/12 et x est le quatrième angle du quadrant.
Solution:
Étant donné, sec x = 13/12
Des identités pythagoriciennes, nous avons,
seconde2x – donc2x = 1
donc2x = seconde2x – 1= (13/12)2- 1
donc2x = (169/144) – 1= 25/144
bronzage x = ± 5/12
Puisque x est le quatrième angle du quadrant, tan x est négatif.
bronzage x = – 5/12
Ainsi, bronzage x = – 5/12
Exemple 3 : Si tan X = 2/3 et tan Y = 1/2, alors quelle est la valeur de tan (X + Y) ?
Solution:
Donné,
bronzage X = 2/3 et bronzage Y = 1/2
Nous savons que,
bronzage (X + Y) = (bronzage X + bronzage Y)/(1 – bronzage X bronzage Y)
bronzage (X + Y) = [(2/3) + (1/2)]/[1 – (2/3)×(1/2)]
= (7/6)/(2/3) = 7/4
Ainsi, bronzage (X + Y) = 7/4
Exemple 4 : Calculez la fonction tangente si les côtés adjacents et opposés d'un triangle rectangle mesurent respectivement 4 cm et 7 cm.
Solution:
modèles de programmation Java
Donné,
Côté adjacent = 4 cm
Côté opposé = 7 cm
Nous savons que,
tan θ = Côté opposé/Côté adjacent
bronzage θ = 7/4 = 1,75
Ainsi, bronzage θ = 1,75
Exemple 5 : Un homme regarde une tour d'horloge à un angle de 60° par rapport au sommet de la tour, dont la hauteur est de 100 m. Quelle est la distance entre l’homme et le pied de la tour ?
Solution:
Donné,
Hauteur de la tour = 100 m et θ = 60°
Soit la distance entre l'homme et le pied de la tour = d
Nous avons,
tan θ = Côté opposé/Côté adjacent
bronzage 60° = 100/j
√3 = 100/j [Depuis, donc 60° = √3]
d = 100/√3
La distance entre l’homme et le pied de la tour est donc 100/√3
Exemple 6 : Trouvez la valeur de tan θ si sin θ = 7/25 et sec θ = 25/24.
Solution:
Donné,
péché θ = 7/25
sec θ = 25/24
Nous savons que,
sec θ = 1/cos θ
25/24 = 1/cos θ cos θ = 24/25
Nous avons,
tan θ = péché θ/cos θ
= (7/25)/(24/25)
= 7/24
Ainsi, bronzage θ = 7/24
Exemple 7 : Trouvez la valeur de tan θ si cosec θ = 5/3 et θ est le premier angle du quadrant.
Solution:
Étant donné, cosec θ = 5/3
Des identités pythagoriciennes, nous avons,
10 ml en oncescosec2θ – lit bébé2θ = 1
lit bébé2θ = cosec2je – 1
lit bébé θ = (5/3)2– 1 = (25/9) – 1 = 16/9
lit bébé θ = ±√16/9 = ± 4/3
Puisque θ est le premier angle du quadrant, les fonctions cotangentes et tangentes sont positives.
lit bébé θ = 4/3
Nous savons que,
lit bébé θ = 1/tan θ
4/3 = 1/tanθ
bronzage θ = 3/4
Ainsi, bronzage θ = 3/4
Exemple 8 : Trouvez tan 3θ si sin θ = 3/7 et θ est le premier angle du quadrant.
Solution :
Étant donné, sin θ = 12/13
Des identités pythagoriciennes que nous avons,
sans2θ + cos2θ = 1
parce que2θ = 1 – péché2θ = 1 – (12/13)2
cos2 θ = 1 – (144/169) = 25/169
cos θ = ±√25/169 = ±5/13
Puisque θ est le premier angle du quadrant, cos θ est positif.
cos θ = 5/13
Nous savons que,
tan θ = péché θ/cos θ
= (12/25)/(5/13) = 12/5
Par conséquent, tan θ = 12/5
Maintenant, nous le savons,
tan 3θ = (3 tan θ – tan3θ) / (1 – 3 tan2θ)
bronzage 3θ = 3 × (12/5)

