Formules Sin Cos en trigonométrie : La trigonométrie, comme son nom l'indique, est l'étude des triangles. Il s'agit d'une branche importante des mathématiques qui étudie la relation entre les longueurs des côtés et les angles du triangle rectangle et aide également à déterminer les longueurs des côtés ou les angles manquants d'un triangle. Il existe six rapports ou fonctions trigonométriques : sinus, cosinus, tangente, cosécante, sécante et cotangente, où cosécante, sécante et cotangente sont les fonctions réciproques des trois autres fonctions, c'est-à-dire respectivement sinus, cosinus et tangente.
Un rapport trigonométrique est défini comme le rapport des longueurs des côtés d'un triangle rectangle. La trigonométrie est utilisée dans divers domaines de notre vie quotidienne. Cela aide à déterminer les hauteurs des collines ou des bâtiments. Il est également utilisé dans des domaines comme la criminologie, la construction, la physique, l'archéologie, l'ingénierie des moteurs marins, etc.
Dans cet article, nous explorerons tout formules de trigonométrie principalement des formules sin et cos avec leurs exemples, et une liste de toutes les formules de trigonométrie.
Table des matières
- Formules en trigonométrie
- Quelques formules de base Sin Cos
- Tableau des formules Sin Cos
- Exemples de formules Sin Cos
- Problèmes pratiques sur les formules Sin Cos en trigonométrie avec des exemples
Formules en trigonométrie
Considérons un triangle rectangle XYZ, où ∠Y = 90°. Soit l'angle au sommet Z θ. Le côté adjacent à θ est appelé côté adjacent et le côté opposé à θ est appelé côté opposé. Une hypoténuse est un côté opposé à l’angle droit ou le côté le plus long d’un angle droit.
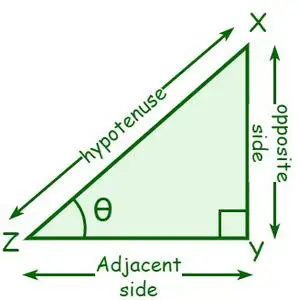
- sin θ = Côté opposé/hypoténuse
- cos θ = Adjacent side/Hypotenuse
- tan θ = Côté opposé/Côté adjacent
- cosec θ = 1/sin θ = Hypotenuse/Opposite side
- sec θ = 1/ cos θ = Hypotenuse/Adjacent side
- lit bébé θ = 1/ beige θ = Côté adjacent/Côté opposé
Formule sinusoïdale
Le sinus d'un angle dans un triangle rectangle est le rapport entre la longueur du côté opposé et la longueur de l'hypoténuse à l'angle donné. Une fonction sinusoïdale est représentée par sin.
sin θ = Côté opposé/hypoténuse
Formule cosinus
Le cosinus d'un angle dans un triangle rectangle est le rapport de la longueur du côté adjacent à la longueur de l'hypoténuse à l'angle donné. Une fonction cosinus est représentée par cos.
tranche Javacos θ = Adjacent side/Hypotenuse
Quelques formules de base Sin Cos
Fonctions sinus et cosinus dans les quadrants
- La fonction sinusoïdale est positive dans les premier et deuxième quadrants et négative dans les troisième et quatrième quadrants.
- La fonction cosinus est positive dans les premier et quatrième quadrants et négative dans les deuxième et troisième quadrants.
Degrés
Quadrant
Fonction signe de sinus
Signe de la fonction Cosinus
0° à 90°
1er quadrant
+ (positif)
+ (positif)
90° à 180°
2ème quadrant
+ (positif)
- (négatif)
180° à 270°
3ème quadrant
- (négatif)
- (négatif)
270° à 360°
4ème quadrant
- (négatif)
+ (positif)
L'identité d'angle négatif des fonctions sinus et cosinus
- Le sinus d’un angle négatif est toujours égal au sinus négatif de l’angle.
péché (– θ) = – péché θ
- Le cosinus d'un angle négatif est toujours égal au cosinus de l'angle.
cos (– θ) = cos θ
Relation entre la fonction sinus et cosinus
sin θ = cos (90° – θ)
Fonctions réciproques des fonctions sinus et cosinus
- Une fonction cosécante est la fonction réciproque de la fonction sinus.
cosec θ = 1/sin θ
- Une fonction sécante est la fonction réciproque de la fonction cosinus.
sec θ = 1/cos θ
Identité pythagoricienne
sans 2 θ + cos 2 θ = 1
Identités périodiques des fonctions sinus et cosinus
péché (θ + 2nπ) = péché θ
cos (θ + 2nπ) = cos θ
Formules double angle pour les fonctions sinus et cosinus
péché 2θ = 2 péché θ cos θ
cos 2θ = cos 2 θ – péché 2 θ = 2 cos 2 θ – 1 = 1 – 2 péché 2 je
Identités de demi-angle pour les fonctions sinus et cosinus
péché (θ/2) = ±√[(1 – cos θ)/2]
cos (θ/2) = ±√[(1 + cos θ)/2]
Identités à triple angle pour les fonctions sinus et cosinus
péché 3θ = 3 péché θ – 4 péché 3 je
cos 3θ = 4cos 3 θ – 3 cos θ
Formules de somme et de différence
- Fonction sinusoïdale
péché (A + B) = péché A cos B + cos A péché B
péché (A – B) = péché A cos B – cos A péché B
- Fonction cosinus
cos (A + B) = cos A cos B – péché A péché B
cos (A – B) = cos A cos B + péché A péché B
Loi des sinus ou règle des sinus
La loi des sinus de la règle des sinus est une loi trigonométrique qui donne une relation entre les longueurs des côtés et les angles d'un triangle.

a/péché A = b/péché B = c/péché C
Où a, b et c sont les longueurs des trois côtés du triangle ABC et A, B et C sont les angles.
Loi des cosinus
La loi des cosinus de la règle du cosinus est utilisée pour déterminer les angles ou les longueurs des côtés manquants ou inconnus d'un triangle.

un 2 =b 2 +c 2 – 2bc cosA
b 2 =c 2 + un 2 – 2ca cosB
c 2 = un 2 + b 2 – 2ab cosC
Où a, b et c sont les longueurs des trois côtés du triangle ABC et A, B et C sont les angles.
Tableau des formules Sin Cos
Voici le tableau/liste des formules Sin et Cos pour différents angles en degrés et en radians :
Liste des formules Sin Cos
| Angle (en degrés) | Angle (en radians) | péché je | cos θ |
|---|---|---|---|
| 0° | 0 | 0 | 1 |
| 30° | p/6 | 1/2 | _3/2 |
| 45° | p/4 | 1/√2 | 1/√2 |
| 60° | p/3 | √3/2 | 1/2 |
| 90° | p/2 | 1 | 0 |
| 120° | 2p/3 | √3/2 | -1/2 |
| 150° | 5p/6 | 1/2 | -√3/2 |
| 180° | Pi | 0 | -1 |
Exemples de formules Sin Cos
Problème 1 : Si cos α = 24/25, alors trouvez la valeur de sin α.
Solution:
Donné,
cosα = 24/25
Des identités pythagoriciennes que nous avons ;
parce que2θ + péché2θ = 1
(24/25)2+ sans2α = 1
sans2α = 1 – (24/25)2
sans2α = 1 – (576/625) = (625 – 576)/625
sans2α = (625 – 576)/625 = 49/626
péché α = √49/625 = ±7/25
Par conséquent, sin α = ±7/25.
Problème 2 : Démontrer les formules sin 2A et cos 2A, si ∠A= 30°.
Solution:
Étant donné, ∠A= 30°
changer de cas javaNous savons que,
1) péché 2A = 2 péché A cos A
sin 2(30°) = 2 sin 30° cos 30°
sin 60° = 2 × (1/2) × (√3/2) {Depuis, sin 30° = 1/2, cos 30° = √3/2 et sin 60° = √3/2}
√3/2 = √3/2
L.H.S = R.H.S
2) cos2A = 2cos2A-1
cos2(30°) = 2cos2(30°) – 1
cos 60° = 2(√3/2)2– 1 = 3/2 – 1 {Depuis, cos 60° = 1/2 et cos 30° = √3/2}
1/2 = 1/2
L.H.S = R.H.S
Donc prouvé.
Problème 3 : Trouver la valeur de cos x, si tan x = 3/4.
Solution:
Étant donné, tan x = 3/4
Nous savons que,
tan x = côté opposé/côté adjacent = 3/4
Pour trouver l'hypoténuse, on utilise le théorème de Pythagore :
hypoténuse2= ci-contre2+ adjacent2
H2= 32+ 42
H2= 9 + 16 = 25
H = √25 = 5
Maintenant, cos x = côté adjacent/hypoténuse
cosx = 4/5
Ainsi, la valeur de cos x est 4/5.
Problème 4 : Trouvez ∠C (en degrés) et ∠A (en degrés), si ∠B = 45°, BC = 15 pouces et AC = 12 pouces.

Solution:
Étant donné : ∠B = 45°, BC = a = 15 pouces et AC = b = 12 pouces.
De la loi des sinus, nous avons
a/péché A = b/péché B = c/péché C
⇒ a/péché A = b/péché B
⇒ 15/péché A = 12/péché 45°
⇒ 15/péché A = 12/(1/√2)
⇒ 15/péché A = 12√2 = 16,97
⇒ sans A = 15/16,97 = 0,8839
⇒ ∠A = péché-1(0,8839) = 62,11°
Nous savons que la somme des angles intérieurs d’un triangle est de 180°.
Donc, ∠A + ∠B + ∠C = 180°
⇒ 62,11° + 45° + ∠C = 180°
⇒ ∠C = 180° – (62,11° + 45°) = 72,89°
Par conséquent, ∠A = 62,11° et ∠C = 72,89°.
Problème 5 : Prouver les identités des demi-angles de la fonction cosinus.
Solution:
L’identité du demi-angle de la fonction cosinus est :
cos (θ/2) = ±√[(1 + cos θ)/2]
Des identités à double angle, nous avons,
cos 2A = 2 cos2A-1
Remplacez maintenant A par θ/2 des deux côtés
⇒ cos 2(θ/2) = 2 cos2(je/2) – 1
⇒ cos θ = 2 cos2(je/2) – 1
⇒ 2cos2(θ/2) = cos θ + 1
⇒ parce que2(θ/2) = (cos θ + 1)/2
⇒ cos (θ/2) = ±√[(1 + cos θ)/2]
Donc prouvé.
Problèmes pratiques sur les formules Sin Cos en trigonométrie avec des exemples
1. Étant donné sin θ = 3/5. Trouvez cos θ.
2. Prouver l'identité sin(2A) = 2 sinA cosA pour A=45∘.
3. Si cos α = 5/13. Trouvez sin(2a).
4. Résolvez θ si sin θ = cos(90∘−θ).
5. Si tan β = 2. Trouvez sin β et cos β en utilisant l'identité pythagoricienne.
FAQ sur les formules Sin Cos en trigonométrie avec exemples
Quelles sont les formules de base du sinus et du cosinus en trigonométrie ?
Les formules de base du sinus et du cosinus sont sin θ = Opposé/Hypoténuse et cos θ = Adjacent/Hypoténuse, où θ est un angle dans un triangle rectangle.
Comment trouver le sinus et le cosinus d’angles spéciaux ?
Les angles spéciaux tels que 0∘, 30∘, 45∘, 60∘ et 90∘ ont des valeurs de sinus et de cosinus spécifiques qui peuvent être mémorisées à l'aide de tables trigonométriques ou de concepts de cercle unitaire.
Quelle est la relation entre les fonctions sinus et cosinus ?
Les fonctions sinus et cosinus sont liées par l'identité péché θ = cos(90∘- θ) et l'identité pythagoricienne sans 2 θ + cos 2 θ = 1.
Comment utilisez-vous les formules des angles doubles pour le sinus et le cosinus ?
Les formules du double angle sont sin(2θ) = 2sinθcosθ et cos(2θ)=cos 2 θ – péché 2 je. Ceux-ci sont utilisés pour exprimer les fonctions trigonométriques d’angles doubles en termes d’angles simples.
Comment trouvez-vous les valeurs du sinus et du cosinus pour les angles dans différents quadrants ?
Les signes des fonctions sinus et cosinus dépendent du quadrant dans lequel se trouve l'angle :
- Premier quadrant : sin θ> 0 et cos θ> 0
- Deuxième quadrant : sin θ> 0 et cos θ <0
- Troisième quadrant : sinθ <0 et cosθ < 0
- Quatrième quadrant : sinθ 0
