Le tracé quantile-quantile (graphique q-q) est une méthode graphique permettant de déterminer si un ensemble de données suit une certaine distribution de probabilité ou si deux échantillons de données proviennent de la même population ou non. Les tracés Q-Q sont particulièrement utiles pour évaluer si un ensemble de données est normalement distribué ou s'il suit une autre distribution connue. Ils sont couramment utilisés dans les statistiques, l'analyse des données et le contrôle qualité pour vérifier les hypothèses et identifier les écarts par rapport aux distributions attendues.
Quantiles et percentiles
Les quantiles sont des points dans un ensemble de données qui divisent les données en intervalles contenant des probabilités ou des proportions égales de la distribution totale. Ils sont souvent utilisés pour décrire la diffusion ou la distribution d’un ensemble de données. Les quantiles les plus courants sont :
- Médian (50e percentile) : La médiane est la valeur médiane d'un ensemble de données lorsqu'il est classé du plus petit au plus grand. Il divise l'ensemble de données en deux moitiés égales.
- Quartiles (25e, 50e et 75e percentiles) : Les quartiles divisent l'ensemble de données en quatre parties égales. Le premier quartile (Q1) est la valeur en dessous de laquelle se situe 25 % des données, le deuxième quartile (Q2) est la médiane et le troisième quartile (Q3) est la valeur en dessous de laquelle se situe 75 % des données.
- Centiles : Les centiles sont similaires aux quartiles mais divisent l'ensemble de données en 100 parties égales. Par exemple, le 90e centile est la valeur en dessous de laquelle se situent 90 % des données.
Note:
- Un tracé q-q est un tracé des quantiles du premier ensemble de données par rapport aux quantiles du deuxième ensemble de données.
- À titre de référence, une ligne de 45 % est également tracée ; Pour si les échantillons proviennent de la même population, alors les points se situent le long de cette ligne.
Distribution normale:
La distribution normale (alias courbe de Bell de distribution gaussienne) est une distribution de probabilité continue représentant la distribution obtenue à partir des valeurs réelles générées aléatoirement.
. 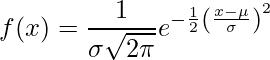

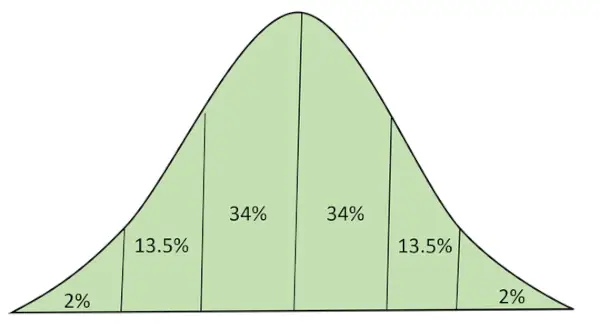
Distribution normale avec aire sous la courbe
Comment dessiner un tracé Q-Q ?
Pour tracer un tracé Quantile-Quantile (Q-Q), vous pouvez suivre ces étapes :
- Collecter les données : Rassemblez l'ensemble de données pour lequel vous souhaitez créer le tracé Q-Q. Assurez-vous que les données sont numériques et représentent un échantillon aléatoire de la population d’intérêt.
- Trier les données : Organisez les données par ordre croissant ou décroissant. Cette étape est essentielle pour calculer avec précision les quantiles.
- Choisissez une distribution théorique : Déterminez la distribution théorique à laquelle vous souhaitez comparer votre ensemble de données. Les choix courants incluent la distribution normale, la distribution exponentielle ou toute autre distribution qui correspond bien à vos données.
- Calculer les quantiles théoriques : Calculez les quantiles pour la distribution théorique choisie. Par exemple, si vous effectuez une comparaison avec une distribution normale, vous utiliserez la fonction de distribution cumulative inverse (CDF) de la distribution normale pour trouver les quantiles attendus.
- Traçage :
- Tracez les valeurs de l'ensemble de données triées sur l'axe des X.
- Tracez les quantiles théoriques correspondants sur l’axe des y.
- Chaque point de données (x, y) représente une paire de valeurs observées et attendues.
- Connectez les points de données pour inspecter visuellement la relation entre l'ensemble de données et la distribution théorique.
Interprétation du tracé QQ
- Si les points du tracé suivent approximativement une ligne droite, cela suggère que votre ensemble de données suit la distribution supposée.
- Les écarts par rapport à la ligne droite indiquent des écarts par rapport à la distribution supposée, nécessitant une enquête plus approfondie.
Explorer la similarité de distribution avec les tracés Q-Q
L'exploration de la similarité de distribution à l'aide de tracés Q-Q est une tâche fondamentale en statistique. Comparer deux ensembles de données pour déterminer s’ils proviennent de la même distribution est vital à diverses fins analytiques. Lorsque l'hypothèse d'une distribution commune est vérifiée, la fusion d'ensembles de données peut améliorer la précision de l'estimation des paramètres, tels que l'emplacement et l'échelle. Les tracés Q-Q, abréviation de tracés quantile-quantile, offrent une méthode visuelle pour évaluer la similarité de distribution. Dans ces graphiques, les quantiles d’un ensemble de données sont comparés aux quantiles d’un autre. Si les points s’alignent étroitement le long d’une ligne diagonale, cela suggère une similitude entre les distributions. Les écarts par rapport à cette ligne diagonale indiquent des différences dans les caractéristiques de distribution.
Alors que des tests comme le chi carré et Kolmogorov-Smirnov les tests peuvent évaluer les différences globales de distribution, les tracés Q-Q fournissent une perspective nuancée en comparant directement les quantiles. Cela permet aux analystes de discerner des différences spécifiques, telles que des changements de lieu ou d'échelle, qui peuvent ne pas être évidentes à partir des seuls tests statistiques formels.
Implémentation Python du tracé QQ
Python3
import> numpy as np> import> matplotlib.pyplot as plt> import> scipy.stats as stats> # Generate example data> np.random.seed(>0>)> data>=> np.random.normal(loc>=>0>, scale>=>1>, size>=>1000>)> # Create Q-Q plot> stats.probplot(data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Normal Q-Q plot'>)> plt.xlabel(>'Theoretical quantiles'>)> plt.ylabel(>'Ordered Values'>)> plt.grid(>True>)> plt.show()> |
>
>
Sortir:
Terrain Q-Q
Ici, comme les points de données suivent approximativement une ligne droite dans le tracé QQ, cela suggère que l'ensemble de données est cohérent avec la distribution théorique supposée, que nous avons supposée dans ce cas être la distribution normale.
Avantages du tracé Q-Q
- Comparaison flexible : Les tracés Q-Q peuvent comparer des ensembles de données de différentes tailles sans exigeant des tailles d’échantillon égales.
- Analyse sans dimension : Ils sont sans dimension, ce qui les rend adaptés à la comparaison d'ensembles de données avec différentes unités ou échelles.
- Interprétation visuelle : Fournit une représentation visuelle claire de la distribution des données par rapport à une distribution théorique.
- Sensible aux écarts : Détecte facilement les écarts par rapport aux distributions supposées, aidant ainsi à identifier les écarts de données.
- Outil de diagnostic : Aide à évaluer les hypothèses de distribution, à identifier les valeurs aberrantes et à comprendre les modèles de données.
Applications du tracé quantile-quantile
Le tracé Quantile-Quantile est utilisé dans le but suivant :
- Évaluation des hypothèses distributionnelles : Les tracés Q-Q sont fréquemment utilisés pour vérifier visuellement si un ensemble de données suit une distribution de probabilité spécifique, telle que la distribution normale. En comparant les quantiles des données observées aux quantiles de la distribution supposée, des écarts par rapport à la distribution supposée peuvent être détectés. Ceci est crucial dans de nombreuses analyses statistiques, où la validité des hypothèses distributionnelles a un impact sur l’exactitude des inférences statistiques.
- Détection des valeurs aberrantes : Les valeurs aberrantes sont des points de données qui s'écartent considérablement du reste de l'ensemble de données. Les tracés Q-Q peuvent aider à identifier les valeurs aberrantes en révélant des points de données qui sont loin du modèle de distribution attendu. Les valeurs aberrantes peuvent apparaître comme des points qui s'écartent de la ligne droite attendue dans le tracé.
- Comparaison des distributions : Les tracés Q-Q peuvent être utilisés pour comparer deux ensembles de données afin de voir s'ils proviennent de la même distribution. Ceci est réalisé en traçant les quantiles d'un ensemble de données par rapport aux quantiles d'un autre ensemble de données. Si les points se situent approximativement le long d’une ligne droite, cela suggère que les deux ensembles de données sont issus de la même distribution.
- Évaluation de la normalité : Les tracés Q-Q sont particulièrement utiles pour évaluer la normalité d'un ensemble de données. Si les points de données du graphique suivent de près une ligne droite, cela indique que l'ensemble de données est à peu près distribué normalement. Les écarts par rapport à la ligne suggèrent des écarts par rapport à la normalité, qui peuvent nécessiter des investigations plus approfondies ou des techniques statistiques non paramétriques.
- Validation du modèle : Dans des domaines comme l'économétrie et l'apprentissage automatique, les tracés Q-Q sont utilisés pour valider les modèles prédictifs. En comparant les quantiles des réponses observées avec les quantiles prédits par un modèle, on peut évaluer dans quelle mesure le modèle s'adapte aux données. Les écarts par rapport au modèle attendu peuvent indiquer des domaines dans lesquels le modèle doit être amélioré.
- Contrôle de qualité : Les tracés Q-Q sont utilisés dans les processus de contrôle qualité pour surveiller la distribution des valeurs mesurées ou observées au fil du temps ou sur différents lots. Les écarts par rapport aux modèles attendus dans le tracé peuvent signaler des changements dans les processus sous-jacents, ce qui incite à une enquête plus approfondie.
Types de tracés QQ
Il existe plusieurs types de tracés Q-Q couramment utilisés dans les statistiques et l'analyse des données, chacun adapté à différents scénarios ou objectifs :
- Distribution normale : Une distribution symétrique où le tracé Q-Q montrerait des points approximativement le long d'une ligne diagonale si les données adhèrent à une distribution normale.
- Distribution asymétrique à droite : Une distribution où le tracé Q-Q afficherait un modèle dans lequel les quantiles observés s'écartent de la ligne droite vers l'extrémité supérieure, indiquant une queue plus longue sur le côté droit.
- Distribution asymétrique à gauche : Une distribution où le tracé Q-Q présenterait un modèle dans lequel les quantiles observés s'écartent de la ligne droite vers l'extrémité inférieure, indiquant une queue plus longue sur le côté gauche.
- Distribution sous-dispersée : Une distribution où le tracé Q-Q montrerait les quantiles observés regroupés plus étroitement autour de la ligne diagonale par rapport aux quantiles théoriques, suggérant une variance plus faible.
- Distribution trop dispersée : Une distribution où le tracé Q-Q afficherait les quantiles observés plus étalés ou s'écartant de la ligne diagonale, indiquant une variance ou une dispersion plus élevée par rapport à la distribution théorique.
Python3
import> numpy as np> import> matplotlib.pyplot as plt> import> scipy.stats as stats> # Generate a random sample from a normal distribution> normal_data>=> np.random.normal(loc>=>0>, scale>=>1>, size>=>1000>)> # Generate a random sample from a right-skewed distribution (exponential distribution)> right_skewed_data>=> np.random.exponential(scale>=>1>, size>=>1000>)> # Generate a random sample from a left-skewed distribution (negative exponential distribution)> left_skewed_data>=> ->np.random.exponential(scale>=>1>, size>=>1000>)> # Generate a random sample from an under-dispersed distribution (truncated normal distribution)> under_dispersed_data>=> np.random.normal(loc>=>0>, scale>=>0.5>, size>=>1000>)> under_dispersed_data>=> under_dispersed_data[(under_dispersed_data>>->1>) & (under_dispersed_data <>1>)]># Truncate> # Generate a random sample from an over-dispersed distribution (mixture of normals)> over_dispersed_data>=> np.concatenate((np.random.normal(loc>=>->2>, scale>=>1>, size>=>500>),> >np.random.normal(loc>=>2>, scale>=>1>, size>=>500>)))> # Create Q-Q plots> plt.figure(figsize>=>(>15>,>10>))> plt.subplot(>2>,>3>,>1>)> stats.probplot(normal_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Normal Distribution'>)> plt.subplot(>2>,>3>,>2>)> stats.probplot(right_skewed_data, dist>=>'expon'>, plot>=>plt)> plt.title(>'Q-Q Plot - Right-skewed Distribution'>)> plt.subplot(>2>,>3>,>3>)> stats.probplot(left_skewed_data, dist>=>'expon'>, plot>=>plt)> plt.title(>'Q-Q Plot - Left-skewed Distribution'>)> plt.subplot(>2>,>3>,>4>)> stats.probplot(under_dispersed_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Under-dispersed Distribution'>)> plt.subplot(>2>,>3>,>5>)> stats.probplot(over_dispersed_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Over-dispersed Distribution'>)> plt.tight_layout()> plt.show()> |
>
>
Sortir:
Graphique Q-Q pour différentes distributions
Preity Zinta
