Étant donné un entier n la tâche est de tout trouver solutions distinctes au problème des n-reines où n les reines sont placées sur un n*n un échiquier tel que deux reines ne puissent pas s'attaquer.
Note: Chaque solution est une configuration unique de n reines représentées comme une permutation de [123....n] . Le numéro au je ème la position indique la rangée de la reine dans le je ème colonne. Par exemple [3142] montre une telle mise en page.
Exemple:
Saisir: n = 4
Sortir: [2 4 1 3] [3 1 4 2]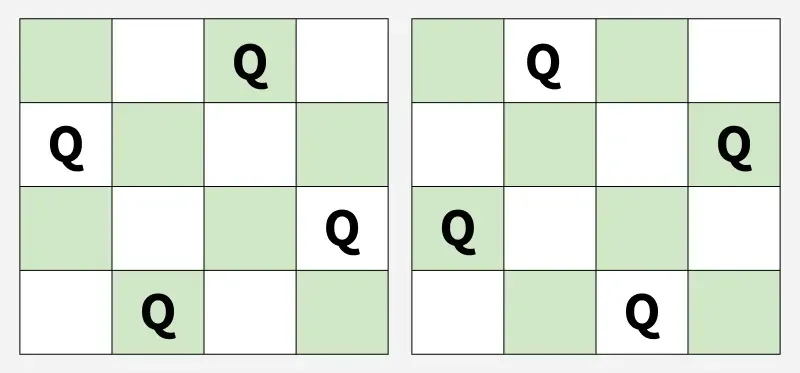
Explication : Ce sont les 2 solutions possibles.Saisir: n = 2
Sortir: []
Explication: Pas de solution puisque les reines peuvent s’attaquer dans toutes les configurations possibles.
Table des matières
- [Approche naïve] En générant toutes les permutations à l'aide de la récursion
- [Approche attendue] Utilisation du retour en arrière avec l'élagage
- [Approche alternative] Retour en arrière à l'aide du masquage de bits
[Approche naïve] - Utilisation de la récursion - O(n! * n) Temps et O(n) Espace
Une idée simple pour résoudre le Problème N-Queens est de générer toutes les permutations possibles de [1 2 3 ...n] puis vérifiez si cela représente une configuration N-Queens valide. Puisque chaque reine doit être dans une ligne et une colonne différentes utiliser automatiquement les permutations prend soin de ces règles. Mais nous devons encore vérifier qu'il n'y a pas deux reines sur le même diagonale.
Ci-dessous est donné le mise en œuvre:
C++//C++ program to find all solution of N queen problem //using recursion #include
//Java program to find all solution of N queen problem //using recursion import java.util.ArrayList; class GfG { // Check if placement is safe static boolean isSafe(ArrayList<Integer> board int currRow int currCol) { for(int i = 0; i < board.size(); i++) { int placedRow = board.get(i); int placedCol = i + 1; // Check diagonals if(Math.abs(placedRow - currRow) == Math.abs(placedCol - currCol)) { return false; // Not safe } } return true; // Safe to place } // Recursive utility to solve static void nQueenUtil(int col int n ArrayList<Integer> board ArrayList<ArrayList<Integer>> res boolean[] visited) { // If all queens placed add to res if(col > n) { res.add(new ArrayList<>(board)); return; } // Try each row in column for(int row = 1; row <= n; row++) { // If row not used if(!visited[row]) { // Check safety if(isSafe(board row col)) { // Mark row visited[row] = true; // Place queen board.add(row); // Recur for next column nQueenUtil(col + 1 n board res visited); // Backtrack board.remove(board.size()-1); visited[row] = false; } } } } // Function to solve N-Queen static ArrayList<ArrayList<Integer>> nQueen(int n) { ArrayList<ArrayList<Integer>> res = new ArrayList<>(); ArrayList<Integer> board = new ArrayList<>(); boolean[] visited = new boolean[n +1]; nQueenUtil(1 n board res visited); return res; } public static void main(String[] args) { int n = 4; ArrayList<ArrayList<Integer>> res = nQueen(n); for(ArrayList<Integer> row : res) { System.out.print('['); for(int i = 0; i < row.size(); i++) { System.out.print(row.get(i)); if(i != row.size()-1) System.out.print(' '); } System.out.println(']'); } } }
#Python program to find all solution of N queen problem #using recursion # Function to check if placement is safe def isSafe(board currRow currCol): for i in range(len(board)): placedRow = board[i] placedCol = i + 1 # Check diagonals if abs(placedRow - currRow) == abs(placedCol - currCol): return False # Not safe return True # Safe to place # Recursive utility to solve N-Queens def nQueenUtil(col n board res visited): # If all queens placed add to res if col > n: res.append(board.copy()) return # Try each row in column for row in range(1 n+1): # If row not used if not visited[row]: # Check safety if isSafe(board row col): # Mark row visited[row] = True # Place queen board.append(row) # Recur for next column nQueenUtil(col+1 n board res visited) # Backtrack board.pop() visited[row] = False # Main N-Queen solver def nQueen(n): res = [] board = [] visited = [False] * (n + 1) nQueenUtil(1 n board res visited) return res if __name__ == '__main__': n = 4 res = nQueen(n) for row in res: print(row)
//C# program to find all solution of N queen problem //using recursion using System; using System.Collections.Generic; class GfG { // Check if placement is safe static bool isSafe(List<int> board int currRow int currCol){ for (int i = 0; i < board.Count; i++) { int placedRow = board[i]; int placedCol = i + 1; // Check diagonals if (Math.Abs(placedRow - currRow) == Math.Abs(placedCol - currCol)) { return false; // Not safe } } return true; // Safe to place } // Recursive utility to solve static void nQueenUtil(int col int n List<int> board List<List<int> > res bool[] visited){ // If all queens placed add to res if (col > n) { res.Add(new List<int>(board)); return; } // Try each row in column for (int row = 1; row <= n; row++) { // If row not used if (!visited[row]) { // Check safety if (isSafe(board row col)) { // Mark row visited[row] = true; // Place queen board.Add(row); // Recur for next column nQueenUtil(col + 1 n board res visited); // Backtrack board.RemoveAt(board.Count - 1); visited[row] = false; } } } } // Main N-Queen solver static List<List<int>> nQueen(int n){ List<List<int> > res = new List<List<int> >(); List<int> board = new List<int>(); bool[] visited = new bool[n + 1]; nQueenUtil(1 n board res visited); return res; } static void Main(string[] args) { int n = 4; List<List<int>> res = nQueen(n); foreach (var temp in res) { Console.WriteLine('[' + String.Join(' ' temp) + ']'); } } }
//JavaScript program to find all solution of N queen problem //using recursion // Function to check if placement is safe function isSafe(board currRow currCol){ for (let i = 0; i < board.length; i++) { let placedRow = board[i]; let placedCol = i + 1; // Check diagonals if (Math.abs(placedRow - currRow) === Math.abs(placedCol - currCol)) { return false; // Not safe } } return true; // Safe to place } // Recursive utility to solve N-Queens function nQueenUtil(col n board res visited){ // If all queens placed add to res if (col > n) { res.push([...board ]); return; } // Try each row in column for (let row = 1; row <= n; row++) { // If row not used if (!visited[row]) { // Check safety if (isSafe(board row col)) { // Mark row visited[row] = true; // Place queen board.push(row); // Recur for next column nQueenUtil(col + 1 n board res visited); // Backtrack board.pop(); visited[row] = false; } } } } // Main N-Queen solver function nQueen(n){ let res = []; let board = []; let visited = Array(n + 1).fill(false); nQueenUtil(1 n board res visited); return res; } // Driver code let n = 4; let res = nQueen(n); res.forEach(row => console.log(row));
Sortir
[2 4 1 3] [3 1 4 2]
Complexité temporelle : O(n!*n) n! pour générer tout permutations et O(n) pour la validation de chaque permutation.
Espace auxiliaire : Sur)
[Approche attendue] - Utilisation du retour en arrière avec l'élagage - O(n!) Time et O(n) Space
Pour optimiser l'approche ci-dessus, nous pouvons utiliser retour en arrière avec la taille . Au lieu de générer toutes les permutations possibles, nous construisons la solution progressivement, tout en nous assurant à chaque étape que la solution partielle reste valide. Si un conflit survient, nous ferons immédiatement marche arrière, cela aide éviter inutile calculs .
Mise en œuvre étape par étape :
- Commencez par la première colonne et essayez de placer une reine dans chaque rangée.
- Conservez les tableaux pour savoir lesquels lignes sont déjà occupés. De même pour le suivi majeur et diagonales mineures sont déjà occupés.
- Si une reine placement conflits avec les reines existantes sauter que rangée et faire marche arrière la reine pour essayer le prochain possible rangée (Élaguer et revenir en arrière pendant un conflit).
// C++ program to find all solution of N queen problem by // using backtracking and pruning #include
// Java program to find all solutions of the N-Queens problem // using backtracking and pruning import java.util.ArrayList; import java.util.List; class GfG { // Utility function for solving the N-Queens // problem using backtracking. static void nQueenUtil(int j int n ArrayList<Integer> board boolean[] rows boolean[] diag1 boolean[] diag2 ArrayList<ArrayList<Integer>> res) { if (j > n) { // A solution is found res.add(new ArrayList<>(board)); return; } for (int i = 1; i <= n; ++i) { if (!rows[i] && !diag1[i + j] && !diag2[i - j + n]) { // Place queen rows[i] = diag1[i + j] = diag2[i - j + n] = true; board.add(i); // Recurse to the next column nQueenUtil(j + 1 n board rows diag1 diag2 res); // Remove queen (backtrack) board.remove(board.size() - 1); rows[i] = diag1[i + j] = diag2[i - j + n] = false; } } } // Solves the N-Queens problem and returns // all valid configurations. static ArrayList<ArrayList<Integer>> nQueen(int n) { ArrayList<ArrayList<Integer>> res = new ArrayList<>(); ArrayList<Integer> board = new ArrayList<>(); // Rows occupied boolean[] rows = new boolean[n + 1]; // Major diagonals (row + j) and Minor diagonals (row - col + n) boolean[] diag1 = new boolean[2 * n + 1]; boolean[] diag2 = new boolean[2 * n + 1]; // Start solving from the first column nQueenUtil(1 n board rows diag1 diag2 res); return res; } public static void main(String[] args) { int n = 4; ArrayList<ArrayList<Integer>> res = nQueen(n); for (ArrayList<Integer> solution : res) { System.out.print('['); for (int i = 0; i < solution.size(); i++) { System.out.print(solution.get(i)); if (i != solution.size() - 1) { System.out.print(' '); } } System.out.println(']'); } } }
# Python program to find all solutions of the N-Queens problem # using backtracking and pruning def nQueenUtil(j n board rows diag1 diag2 res): if j > n: # A solution is found res.append(board[:]) return for i in range(1 n + 1): if not rows[i] and not diag1[i + j] and not diag2[i - j + n]: # Place queen rows[i] = diag1[i + j] = diag2[i - j + n] = True board.append(i) # Recurse to the next column nQueenUtil(j + 1 n board rows diag1 diag2 res) # Remove queen (backtrack) board.pop() rows[i] = diag1[i + j] = diag2[i - j + n] = False def nQueen(n): res = [] board = [] # Rows occupied rows = [False] * (n + 1) # Major diagonals (row + j) and Minor diagonals (row - col + n) diag1 = [False] * (2 * n + 1) diag2 = [False] * (2 * n + 1) # Start solving from the first column nQueenUtil(1 n board rows diag1 diag2 res) return res if __name__ == '__main__': n = 4 res = nQueen(n) for temp in res: print(temp)
// C# program to find all solutions of the N-Queens problem // using backtracking and pruning using System; using System.Collections.Generic; class GfG { // Utility function for solving the N-Queens // problem using backtracking. static void nQueenUtil(int j int n List<int> board bool[] rows bool[] diag1 bool[] diag2 List<List<int>> res) { if (j > n) { // A solution is found res.Add(new List<int>(board)); return; } for (int i = 1; i <= n; ++i) { if (!rows[i] && !diag1[i + j] && !diag2[i - j + n]) { // Place queen rows[i] = diag1[i + j] = diag2[i - j + n] = true; board.Add(i); // Recurse to the next column nQueenUtil(j + 1 n board rows diag1 diag2 res); // Remove queen (backtrack) board.RemoveAt(board.Count - 1); rows[i] = diag1[i + j] = diag2[i - j + n] = false; } } } // Solves the N-Queens problem and returns // all valid configurations. static List<List<int>> nQueen(int n) { List<List<int>> res = new List<List<int>>(); List<int> board = new List<int>(); // Rows occupied bool[] rows = new bool[n + 1]; // Major diagonals (row + j) and Minor diagonals (row - col + n) bool[] diag1 = new bool[2 * n + 1]; bool[] diag2 = new bool[2 * n + 1]; // Start solving from the first column nQueenUtil(1 n board rows diag1 diag2 res); return res; } static void Main(string[] args) { int n = 4; List<List<int>> res = nQueen(n); foreach (var temp in res) { Console.WriteLine('[' + String.Join(' ' temp) + ']'); } } }
// JavaScript program to find all solutions of the N-Queens problem // using backtracking and pruning // Utility function for solving the N-Queens // problem using backtracking. function nQueenUtil(j n board rows diag1 diag2 res) { if (j > n) { // A solution is found res.push([...board]); return; } for (let i = 1; i <= n; ++i) { if (!rows[i] && !diag1[i + j] && !diag2[i - j + n]) { // Place queen rows[i] = diag1[i + j] = diag2[i - j + n] = true; board.push(i); // Recurse to the next column nQueenUtil(j + 1 n board rows diag1 diag2 res); // Remove queen (backtrack) board.pop(); rows[i] = diag1[i + j] = diag2[i - j + n] = false; } } } // Solves the N-Queens problem and returns // all valid configurations. function nQueen(n) { const res = []; const board = []; // Rows occupied const rows = Array(n + 1).fill(false); // Major diagonals (row + j) and Minor diagonals (row - col + n) const diag1 = Array(2 * n + 1).fill(false); const diag2 = Array(2 * n + 1).fill(false); // Start solving from the first column nQueenUtil(1 n board rows diag1 diag2 res); return res; } // Driver Code const n = 4; const res = nQueen(n); res.forEach(temp => console.log(temp));
Sortir
[2 4 1 3] [3 1 4 2]
Complexité temporelle : O(n!) Pour générer tout permutations .
Espace auxiliaire : Sur)
[Approche alternative] - Retour en arrière à l'aide du masquage de bits
Pour optimiser davantage le retour en arrière approche en particulier pour des valeurs plus grandes de n nous pouvons utiliser masquage de bits pour suivre efficacement occupé rangées et diagonales. Masquage de bits nous permet d'utiliser des entiers ( lignes ld rd ) pour suivre les lignes et les diagonales occupées en utilisant la fonction rapide opérations au niveau du bit pour plus rapide calculs. L'approche reste la même que ci-dessus.
Ci-dessous est donné le mise en œuvre:
C++//C++ program to find all solution of N queen problem //using recursion #include
// Java program to find all solution of N queen problem // using recursion import java.util.*; class GfG { // Function to check if the current placement is safe static boolean isSafe(int row int col int rows int ld int rd int n) { return !(((rows >> row) & 1) == 1) && !(((ld >> (row + col)) & 1) == 1) && !(((rd >> (row - col + n)) & 1) == 1); } // Recursive function to generate all possible permutations static void nQueenUtil(int col int n ArrayList<Integer> board ArrayList<ArrayList<Integer>> res int rows int ld int rd) { // If all queens are placed add into res if (col > n) { res.add(new ArrayList<>(board)); return; } // Try placing a queen in each row // of the current column for (int row = 1; row <= n; ++row) { // Check if it's safe to place the queen if (isSafe(row col rows ld rd n)) { // Place the queen board.add(row); // Recur to place the next queen nQueenUtil(col + 1 n board res rows | (1 << row) (ld | (1 << (row + col))) (rd | (1 << (row - col + n)))); // Backtrack: remove the queen board.remove(board.size() - 1); } } } // Main function to find all distinct // res to the n-queens puzzle static ArrayList<ArrayList<Integer>> nQueen(int n) { ArrayList<ArrayList<Integer>> res = new ArrayList<>(); // Current board configuration ArrayList<Integer> board = new ArrayList<>(); // Start solving from the first column nQueenUtil(1 n board res 0 0 0); return res; } public static void main(String[] args) { int n = 4; ArrayList<ArrayList<Integer>> res = nQueen(n); for (ArrayList<Integer> solution : res) { System.out.print('['); for (int j = 0; j < n; ++j) { System.out.print(solution.get(j)); if (j != n - 1) System.out.print(' '); } System.out.println(']'); } } }
# Python program to find all solution of N queen problem # using recursion # Function to check if the current placement is safe def isSafe(row col rows ld rd n): return not ((rows >> row) & 1) and not ((ld >> (row + col)) & 1) and not ((rd >> (row - col + n)) & 1) # Recursive function to generate all possible permutations def nQueenUtil(col n board res rows ld rd): # If all queens are placed add into res if col > n: res.append(board[:]) return # Try placing a queen in each row # of the current column for row in range(1 n + 1): # Check if it's safe to place the queen if isSafe(row col rows ld rd n): # Place the queen board.append(row) # Recur to place the next queen nQueenUtil(col + 1 n board res rows | (1 << row) (ld | (1 << (row + col))) (rd | (1 << (row - col + n)))) # Backtrack: remove the queen board.pop() # Main function to find all distinct # res to the n-queens puzzle def nQueen(n): res = [] # Current board configuration board = [] # Start solving from the first column nQueenUtil(1 n board res 0 0 0) return res if __name__ == '__main__': n = 4 res = nQueen(n) for solution in res: print('[' end='') for j in range(n): print(solution[j] end='') if j != n - 1: print(' ' end='') print(']')
// C# program to find all solution of N queen problem // using recursion using System; using System.Collections.Generic; class GfG { // Function to check if the current placement is safe static bool isSafe(int row int col int rows int ld int rd int n) { return !(((rows >> row) & 1) == 1) && !(((ld >> (row + col)) & 1) == 1) && !(((rd >> (row - col + n)) & 1) == 1); } // Recursive function to generate all possible permutations static void nQueenUtil(int col int n List<int> board List<List<int>> res int rows int ld int rd) { // If all queens are placed add into res if (col > n) { res.Add(new List<int>(board)); return; } // Try placing a queen in each row // of the current column for (int row = 1; row <= n; ++row) { // Check if it's safe to place the queen if (isSafe(row col rows ld rd n)) { // Place the queen board.Add(row); // Recur to place the next queen nQueenUtil(col + 1 n board res rows | (1 << row) (ld | (1 << (row + col))) (rd | (1 << (row - col + n)))); // Backtrack: remove the queen board.RemoveAt(board.Count - 1); } } } // Main function to find all distinct // res to the n-queens puzzle static List<List<int>> nQueen(int n) { List<List<int>> res = new List<List<int>>(); // Current board configuration List<int> board = new List<int>(); // Start solving from the first column nQueenUtil(1 n board res 0 0 0); return res; } static void Main() { int n = 4; List<List<int>> res = nQueen(n); foreach (var solution in res) { Console.Write('['); for (int j = 0; j < n; ++j) { Console.Write(solution[j]); if (j != n - 1) Console.Write(' '); } Console.WriteLine(']'); } } }
// JavaScript program to find all solution of N queen problem // using recursion // Function to check if the current placement is safe function isSafe(row col rows ld rd n) { return !((rows >> row) & 1) && !((ld >> (row + col)) & 1) && !((rd >> (row - col + n)) & 1); } // Recursive function to generate all possible permutations function nQueenUtil(col n board res rows ld rd) { // If all queens are placed add into res if (col > n) { res.push([...board]); return; } // Try placing a queen in each row // of the current column for (let row = 1; row <= n; ++row) { // Check if it's safe to place the queen if (isSafe(row col rows ld rd n)) { // Place the queen board.push(row); // Recur to place the next queen nQueenUtil(col + 1 n board res rows | (1 << row) (ld | (1 << (row + col))) (rd | (1 << (row - col + n)))); // Backtrack: remove the queen board.pop(); } } } // Main function to find all distinct // res to the n-queens puzzle function nQueen(n) { let res = []; // Current board configuration let board = []; // Start solving from the first column nQueenUtil(1 n board res 0 0 0); return res; } // Driver Code let n = 4; let res = nQueen(n); for (let i = 0; i < res.length; i++) { process.stdout.write('['); for (let j = 0; j < n; ++j) { process.stdout.write(res[i][j].toString()); if (j !== n - 1) process.stdout.write(' '); } console.log(']'); }
Sortir
[2 4 1 3] [3 1 4 2]
Complexité temporelle : O(n!) pour générer toutes les permutations.
Complexité spatiale : Sur)
