Étant donné une chaîne, trouvez toutes les façons de briser la chaîne donnée sous forme de support. Encluant chaque sous-chaîne dans une parenthèse.
instruction if-else java
Exemples:
Input : abc Output: (a)(b)(c) (a)(bc) (ab)(c) (abc) Input : abcd Output : (a)(b)(c)(d) (a)(b)(cd) (a)(bc)(d) (a)(bcd) (ab)(c)(d) (ab)(cd) (abc)(d) (abcd)
Nous vous recommandons fortement de minimiser votre navigateur et de l'essayer vous-même d'abord.
L'idée est d'utiliser la récursivité. Nous maintenons deux paramètres - index du caractère suivant à traiter et la chaîne de sortie jusqu'à présent. Nous commençons à partir de l'index du caractère suivant pour être traité sous-chaîne d'ajout formé par chaîne non transformée à la chaîne de sortie et recursions sur la chaîne restante jusqu'à ce que nous traitions toute la chaîne. Nous utilisons STD :: substr pour former la chaîne de sortie. substr (pos n) renvoie une sous-chaîne de longueur n qui commence à la position pos de la chaîne de courant.
Le diagramme ci-dessous montre une arborescence de récursivité pour la chaîne d'entrée «ABC». Chaque nœud sur le diagramme affiche une chaîne traitée (marquée par vert) et une chaîne non transformée (marquée par rouge).
charat java
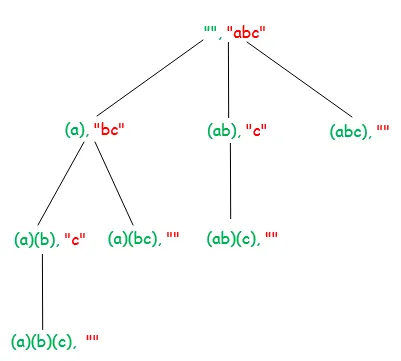
Vous trouverez ci-dessous la mise en œuvre de l'idée ci-dessus
C++// C++ Program to find all combinations of Non- // overlapping substrings formed from given // string #include
// Java program to find all combinations of Non- // overlapping substrings formed from given // string class GFG { // find all combinations of non-overlapping // substrings formed by input string str static void findCombinations(String str int index String out) { if (index == str.length()) System.out.println(out); for (int i = index; i < str.length(); i++) // append substring formed by str[index // i] to output string findCombinations(str i + 1 out + '(' + str.substring(index i+1) + ')' ); } // Driver Code public static void main (String[] args) { // input string String str = 'abcd'; findCombinations(str 0 ''); } } // Contributed by Pramod Kumar
# Python3 Program to find all combinations of Non- # overlapping substrings formed from given # string # find all combinations of non-overlapping # substrings formed by input string str # index – index of the next character to # be processed # out - output string so far def findCombinations(string index out): if index == len(string): print(out) for i in range(index len(string) 1): # append substring formed by str[index # i] to output string findCombinations(string i + 1 out + '(' + string[index:i + 1] + ')') # Driver Code if __name__ == '__main__': # input string string = 'abcd' findCombinations(string 0 '') # This code is contributed by # sanjeev2552
// C# program to find all combinations // of Non-overlapping substrings formed // from given string using System; class GFG { // find all combinations of non-overlapping // substrings formed by input string str public static void findCombinations(string str int index string @out) { if (index == str.Length) { Console.WriteLine(@out); } for (int i = index; i < str.Length; i++) { // append substring formed by // str[index i] to output string findCombinations( str i + 1 @out + '(' + str.Substring(index (i + 1) - index) + ')'); } } // Driver Code public static void Main(string[] args) { // input string string str = 'abcd'; findCombinations(str 0 ''); } } // This code is contributed by Shrikant13
// Javascript program for the above approach // find all combinations of non-overlapping // substrings formed by input string str // index – index of the next character to // be processed // out - output string so far function findCombinations(string index out) { if (index == string.length) { console.log(out); } for (let i = index; i < string.length; i++) { // append substring formed by str[index // i] to output string findCombinations(string i + 1 out + '(' + string.substring(index i + 1) + ')'); } } // Driver Code const string = 'abcd'; findCombinations(string 0 ''); // contributed by adityasharmadev01
Sortir
(a)(b)(c)(d) (a)(b)(cd) (a)(bc)(d) (a)(bcd) (ab)(c)(d) (ab)(cd) (abc)(d) (abcd)
Complexité du temps: o (n2)
Espace auxiliaire: o (n2)
Codes couleurs Java
