En informatique, il existe des problèmes dont les solutions ne sont pas encore trouvées, les problèmes sont divisés en classes appelées Cours de complexité . Dans la théorie de la complexité, une classe de complexité est un ensemble de problèmes de complexité connexe. Ces cours aident les scientifiques à regrouper les problèmes en fonction du temps et de l'espace dont ils ont besoin pour résoudre les problèmes et vérifier les solutions. C'est la branche de la théorie du calcul qui traite des ressources nécessaires pour résoudre un problème.
conversion d'entier en chaîne
Les ressources communes sont le temps et l’espace, c’est-à-dire le temps nécessaire à l’algorithme pour résoudre un problème et l’utilisation de la mémoire correspondante.
- La complexité temporelle d’un algorithme est utilisée pour décrire le nombre d’étapes nécessaires pour résoudre un problème, mais elle peut également être utilisée pour décrire le temps nécessaire pour vérifier la réponse.
- La complexité spatiale d'un algorithme décrit la quantité de mémoire nécessaire au fonctionnement de l'algorithme.
Les cours de complexité sont utiles pour organiser des types de problèmes similaires.
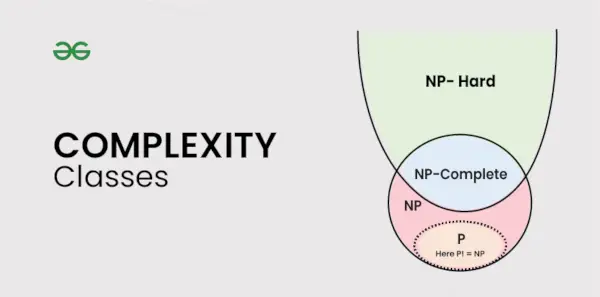
Types de classes de complexité
Cet article traite des classes de complexité suivantes :
- Classe P
- Classe NP
- Classe CoNP
- NP-dur
- NP-complet
Classe P
Le P dans la classe P signifie Temps polynomial. C'est l'ensemble des problèmes de décision (problèmes avec réponse oui ou non) qui peuvent être résolus par une machine déterministe en temps polynomial.
Caractéristiques:
- La solution à Problème P s est facile à trouver.
- P. est souvent une classe de problèmes informatiques qui peuvent être résolus et traités. Traitable signifie que les problèmes peuvent être résolus en théorie comme en pratique. Mais les problèmes qui peuvent être résolus en théorie mais pas en pratique sont réputés insolubles.
Cette classe contient de nombreux problèmes :
- Calculer le plus grand diviseur commun.
- Trouver une correspondance maximale.
- Tri par fusion
Classe NP
Le NP dans la classe NP signifie Temps polynomial non déterministe . C'est un ensemble de problèmes de décision qui peuvent être résolus par une machine non déterministe en temps polynomial.
Caractéristiques:
- Les solutions de la classe NP sont difficiles à trouver puisqu’elles sont résolues par une machine non déterministe mais les solutions sont faciles à vérifier.
- Les problèmes de NP peuvent être vérifiés par une machine de Turing en temps polynomial.
Exemple:
Prenons un exemple pour mieux comprendre Classe NP . Supposons qu'il existe une entreprise ayant un total de 1000 employés ayant un employé unique identifiants . Supposons qu'il y ait 200 chambres à leur disposition. Une sélection de 200 les employés doivent être jumelés, mais le PDG de l’entreprise dispose des données de certains employés qui ne peuvent pas travailler dans la même pièce pour des raisons personnelles.
Ceci est un exemple de PAR EXEMPLE problème. Puisqu'il est facile de vérifier si le choix donné 200 les employés proposés par un collègue sont satisfaisants ou non c'est-à-dire qu'aucun couple tiré de la liste des collègues n'apparaît sur la liste donnée par le PDG. Mais générer une telle liste à partir de zéro semble être si difficile qu’il est totalement irréaliste.
Cela indique que si quelqu’un peut nous fournir la solution au problème, nous pouvons trouver la paire correcte et incorrecte en temps polynomial. Ainsi pour le PAR EXEMPLE problème de classe, la réponse est possible, qui peut être calculée en temps polynomial.
formatage de chaîne Java
Cette classe contient de nombreux problèmes que l'on aimerait pouvoir résoudre efficacement :
- Problème de satisfiabilité booléenne (SAT).
- Problème de chemin hamiltonien.
- Coloration du graphique.
Classe Co-NP
Co-NP signifie le complément de la classe NP. Cela signifie que si la réponse à un problème en Co-NP est Non, alors il existe une preuve qui peut être vérifiée en temps polynomial.
Caractéristiques:
- Si un problème X est dans NP, alors son complément X’ est aussi dans CoNP.
- Pour un problème NP et CoNP, il n'est pas nécessaire de vérifier toutes les réponses d'un coup en temps polynomial, il est nécessaire de vérifier une seule réponse particulière oui ou non en temps polynomial pour qu'un problème soit en NP ou CoNP.
Voici quelques exemples de problèmes pour CoNP :
- Pour vérifier un nombre premier.
- Factorisation entière.
Classe NP-difficile
Un problème NP-difficile est au moins aussi difficile que le problème le plus difficile de NP et c'est une classe de problèmes telle que chaque problème de NP se réduit à NP-difficile.
Caractéristiques:
formater la date en chaîne
- Tous les problèmes NP-difficiles ne sont pas dans NP.
- Il faut beaucoup de temps pour les vérifier. Cela signifie que si une solution à un problème NP-difficile est donnée, il faudra beaucoup de temps pour vérifier si elle est correcte ou non.
- Un problème A est dans NP-difficile si, pour tout problème L dans NP, il existe une réduction en temps polynomial de L à A.
Voici quelques exemples de problèmes dans Np-hard :
- Problème d'arrêt.
- Formules booléennes qualifiées.
- Pas de cycle hamiltonien.
Classe NP-complète
Un problème est NP-complet s’il est à la fois NP et NP-difficile. Les problèmes NP-complets sont les problèmes difficiles de NP.
Caractéristiques:
- Les problèmes NP-complets sont particuliers car tout problème de la classe NP peut être transformé ou réduit en problèmes NP-complets en temps polynomial.
- Si l’on pouvait résoudre un problème NP-complet en temps polynomial, alors on pourrait également résoudre n’importe quel problème NP en temps polynomial.
Voici quelques exemples de problèmes :
- Cycle hamiltonien.
- Satisfiabilité.
- Couverture du sommet .
| Classe de complexité | Caractéristique |
| P. | Facilement résoluble en temps polynomial. |
| PAR EXEMPLE | Oui, les réponses peuvent être vérifiées en temps polynomial. |
| Co-NP | Non, les réponses peuvent être vérifiées en temps polynomial. |
| NP-dur | Tous les problèmes NP-difficiles ne sont pas dans NP et leur vérification prend beaucoup de temps. |
| NP-complet | Un problème NP et NP-difficile est NP-complet. |
