Coût minimum pour découper une planche en carrés
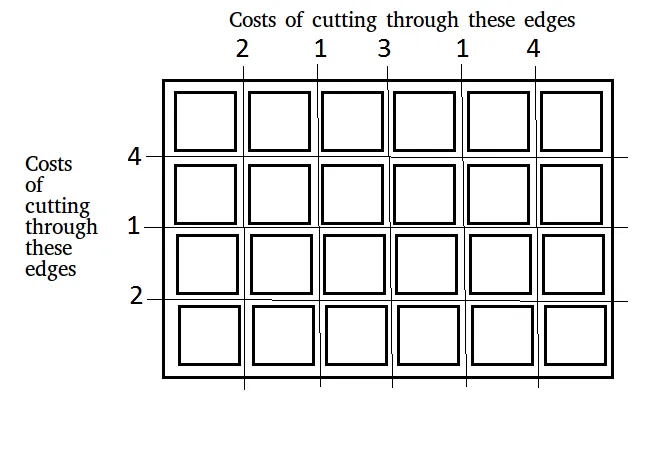
Étant donné une planche de dimensions n × m qui doit être découpé en n × m carrés. Le coût de réalisation d'une coupe le long d'un bord horizontal ou vertical est divisé en deux tableaux :
- x[] : Réduction des coûts le long des bords verticaux (dans le sens de la longueur).
- et[] : Réduire les coûts le long des bords horizontaux (dans le sens de la largeur).
Trouvez le coût total minimum requis pour découper la planche en carrés de manière optimale.
Exemples :
Saisir: x[] = [2 1 3 1 4] y[] = [4 1 2] n = 4 m = 6
Sortir: 42
Explication:
Au départ non. de segments horizontaux = 1 & non. de segments verticaux = 1.
La façon optimale de couper en carré est :
Choisissez 4 (parmi x) -> coupe verticale Coût = 4 × segments horizontaux = 4
Maintenant segments horizontaux = 1 segments verticaux = 2.
Choisissez 4 (sur y) -> coupe horizontale Coût = 4 × segments verticaux = 8
Maintenant segments horizontaux = 2 segments verticaux = 2.
Choisissez-en 3 (parmi x) -> coupe verticale Coût = 3 × segments horizontaux = 6
Maintenant segments horizontaux = 2 segments verticaux = 3.
Choisissez 2 (parmi x) -> coupe verticale Coût = 2 × segments horizontaux = 4
Maintenant segments horizontaux = 2 segments verticaux = 4.
Choisissez 2 (sur y) -> coupe horizontale Coût = 2 × segments verticaux = 8
Maintenant segments horizontaux = 3 segments verticaux = 4.
Choisissez 1 (parmi x) -> coupe verticale Coût = 1 × segments horizontaux = 3
Maintenant segments horizontaux = 3 segments verticaux = 5.
Choisissez 1 (parmi x) -> coupe verticale Coût = 1 × segments horizontaux = 3
Maintenant segments horizontaux = 3 segments verticaux = 6.
Choisissez 1 (sur y) -> coupe horizontale Coût = 1 × segments verticaux = 6
Maintenant segments horizontaux = 4 segments verticaux = 6.
Donc le coût total = 4 + 8 + 6 + 4 + 8 + 3 + 3 + 6 = 42.Saisir: x[] = [1 1 1] y[] = [1 1 1] n = 4 m = 4
Sortir: 15
Explication:
Au départ non. de segments horizontaux = 1 & non. de segments verticaux = 1.
La façon optimale de couper en carré est :
Choisissez 1 (sur y) -> coupe horizontale Coût = 1 × segments verticaux = 1
Maintenant segments horizontaux = 2 segments verticaux = 1.
Choisissez 1 (sur y) -> coupe horizontale Coût = 1 × segments verticaux = 1
Maintenant segments horizontaux = 3 segments verticaux = 1.
Choisissez 1 (sur y) -> coupe horizontale Coût = 1 × segments verticaux = 1
Maintenant segments horizontaux = 4 segments verticaux = 1.
Choisissez 1 (parmi x) -> coupe verticale Coût = 1 × segments horizontaux = 4
Maintenant segments horizontaux = 4 segments verticaux = 2.
Choisissez 1 (parmi x) -> coupe verticale Coût = 1 × segments horizontaux = 4
Maintenant segments horizontaux = 4 segments verticaux = 3.
Choisissez 1 (parmi x) -> coupe verticale Coût = 1 × segments horizontaux = 4
Maintenant segments horizontaux = 4 segments verticaux = 4
Donc le coût total = 1 + 1 + 1 + 4 + 4 + 4 = 15.
Table des matières
- [Approche naïve] Essayez toutes les permutations - O((n+m)!×(n+m)) Temps et O(n+m) Espace
- [Approche attendue] Utilisation de la technique gourmande - O (n (log n) + m (log m)) Temps et O (1) Espace
[Approche naïve] Essayez toutes les permutations - O((n+m)!×(n+m)) Temps et O(n+m) Espace
L'idée est de générer toutes les permutations possibles des coupes données, puis de calculer le coût de chaque permutation. Renvoyez enfin le coût minimum parmi eux.
Note: Cette approche n'est pas réalisable pour des entrées plus importantes car le nombre de permutations augmente factoriellement comme (m+n-2) !.
Pour chaque permutation, nous devons calculer le coût en temps O(m+n). Par conséquent, la complexité temporelle globale devient O((m+n−2)!×(m+n)).
[Approche attendue] Utilisation de la technique gourmande - O (n (log n) + m (log m)) Temps et O (1) Espace
L'idée est de réaliser d'abord les coupes les plus coûteuses à l'aide d'un approche gourmande . L’observation est que le choix de la réduction de coût la plus élevée à chaque étape réduit les coûts futurs en affectant plusieurs éléments à la fois. Nous trions les coûts de réduction verticaux (x) et horizontaux (y) par ordre décroissant, puis sélectionnons de manière itérative le plus important pour maximiser les économies de coûts. Les coupes restantes sont traitées séparément pour garantir que toutes les sections sont divisées de manière optimale.
Que se passe-t-il lorsque nous effectuons une coupe ?
- Coupe horizontale → vous coupez dans le sens de la largeur donc le nombre de bandes horizontales augmente (hCount++). Mais le coût est multiplié par vCount (le nombre de bandes verticales) car la coupe horizontale doit traverser tous les segments verticaux.
- Coupe verticale → vous coupez en hauteur donc le nombre de bandes verticales augmente (vCount++). Mais le coût est multiplié par hCount (le nombre de bandes horizontales) car la coupe verticale doit traverser tous les segments horizontaux.
Étapes pour résoudre le problème :
- Triez les tableaux x et y par ordre décroissant.
- Utilisez deux pointeurs, un pour x et un pour y, en commençant par la valeur la plus élevée et en progressant vers des valeurs plus petites.
- Maintenez hCount et vCount pour suivre le nombre de segments affectés par chaque coupe et mettez-les à jour en conséquence.
- Répétez pendant que x et y ont des coupes non traitées en choisissant toujours le coût le plus élevé pour minimiser les dépenses globales.
- Si x il reste des coupes, traitez-les avec le multiplicateur hCount ; traitez de la même manière les coupes y restantes avec vCount.
- Accumulez le coût total à chaque étape à l'aide de la formule : réduction du coût * nombre de pièces concernées garantissant un coût minimal.
#include #include #include using namespace std ; int minCost ( int n int m vector < int >& x vector < int >& y ) { // Sort the cutting costs in ascending order sort ( x . begin () x . end ()); sort ( y . begin () y . end ()); int hCount = 1 vCount = 1 ; int i = x . size () - 1 j = y . size () - 1 ; int totalCost = 0 ; while ( i >= 0 && j >= 0 ) { // Choose the larger cost cut to // minimize future costs if ( x [ i ] >= y [ j ]) { totalCost += x [ i ] * hCount ; vCount ++ ; i -- ; } else { totalCost += y [ j ] * vCount ; hCount ++ ; j -- ; } } // Process remaining vertical cuts while ( i >= 0 ) { totalCost += x [ i ] * hCount ; vCount ++ ; i -- ; } // Process remaining horizontal cuts while ( j >= 0 ) { totalCost += y [ j ] * vCount ; hCount ++ ; j -- ; } return totalCost ; } int main () { int n = 4 m = 6 ; vector < int > x = { 2 1 3 1 4 }; vector < int > y = { 4 1 2 }; cout < < minCost ( n m x y ) < < endl ; return 0 ; }
Java import java.util.Arrays ; class GfG { static int minCost ( int n int m int [] x int [] y ) { // Sort the cutting costs in ascending order Arrays . sort ( x ); Arrays . sort ( y ); int hCount = 1 vCount = 1 ; int i = x . length - 1 j = y . length - 1 ; int totalCost = 0 ; while ( i >= 0 && j >= 0 ) { // Choose the larger cost cut to // minimize future costs if ( x [ i ] >= y [ j ] ) { totalCost += x [ i ] * hCount ; vCount ++ ; i -- ; } else { totalCost += y [ j ] * vCount ; hCount ++ ; j -- ; } } // Process remaining vertical cuts while ( i >= 0 ) { totalCost += x [ i ] * hCount ; vCount ++ ; i -- ; } // Process remaining horizontal cuts while ( j >= 0 ) { totalCost += y [ j ] * vCount ; hCount ++ ; j -- ; } return totalCost ; } public static void main ( String [] args ) { int n = 4 m = 6 ; int [] x = { 2 1 3 1 4 }; int [] y = { 4 1 2 }; System . out . println ( minCost ( n m x y )); } }
Python def minCost ( n m x y ): # Sort the cutting costs in ascending order x . sort () y . sort () hCount vCount = 1 1 i j = len ( x ) - 1 len ( y ) - 1 totalCost = 0 while i >= 0 and j >= 0 : # Choose the larger cost cut to # minimize future costs if x [ i ] >= y [ j ]: totalCost += x [ i ] * hCount vCount += 1 i -= 1 else : totalCost += y [ j ] * vCount hCount += 1 j -= 1 # Process remaining vertical cuts while i >= 0 : totalCost += x [ i ] * hCount vCount += 1 i -= 1 # Process remaining horizontal cuts while j >= 0 : totalCost += y [ j ] * vCount hCount += 1 j -= 1 return totalCost if __name__ == '__main__' : n m = 4 6 x = [ 2 1 3 1 4 ] y = [ 4 1 2 ] print ( minCost ( n m x y ))
C# using System ; class GfG { public static int minCost ( int n int m int [] x int [] y ) { // Sort the cutting costs in ascending order Array . Sort ( x ); Array . Sort ( y ); int hCount = 1 vCount = 1 ; int i = x . Length - 1 j = y . Length - 1 ; int totalCost = 0 ; // Process the cuts in greedy manner while ( i >= 0 && j >= 0 ) { // Choose the larger cost cut to // minimize future costs if ( x [ i ] >= y [ j ]) { totalCost += x [ i ] * hCount ; vCount ++ ; i -- ; } else { totalCost += y [ j ] * vCount ; hCount ++ ; j -- ; } } // Process remaining vertical cuts while ( i >= 0 ) { totalCost += x [ i ] * hCount ; vCount ++ ; i -- ; } // Process remaining horizontal cuts while ( j >= 0 ) { totalCost += y [ j ] * vCount ; hCount ++ ; j -- ; } return totalCost ; } public static void Main () { int n = 4 m = 6 ; int [] x = { 2 1 3 1 4 }; int [] y = { 4 1 2 }; Console . WriteLine ( minCost ( n m x y )); } }
JavaScript function minCost ( n m x y ) { // Sort the cutting costs in ascending order x . sort (( a b ) => a - b ); y . sort (( a b ) => a - b ); let hCount = 1 vCount = 1 ; let i = x . length - 1 j = y . length - 1 ; let totalCost = 0 ; while ( i >= 0 && j >= 0 ) { // Choose the larger cost cut to // minimize future costs if ( x [ i ] >= y [ j ]) { totalCost += x [ i ] * hCount ; vCount ++ ; i -- ; } else { totalCost += y [ j ] * vCount ; hCount ++ ; j -- ; } } // Process remaining vertical cuts while ( i >= 0 ) { totalCost += x [ i ] * hCount ; vCount ++ ; i -- ; } // Process remaining horizontal cuts while ( j >= 0 ) { totalCost += y [ j ] * vCount ; hCount ++ ; j -- ; } return totalCost ; } // Driver Code let n = 4 m = 6 ; let x = [ 2 1 3 1 4 ]; let y = [ 4 1 2 ]; console . log ( minCost ( n m x y ));
Sortir
42
