ANCÊTRE COMMUN LE PLUS BAS DANS UN ARBRE BINAIRE - TECHCODEVIEW.COM

Quel est l’ancêtre commun le plus bas dans l’arbre binaire ?

Le ancêtre commun le plus bas est le nœud le plus bas de l'arbre qui a à la fois n1 et n2 comme descendance, où n1 et n2 sont les nœuds pour lesquels on souhaite trouver la LCA. Par conséquent, l’ACV d’un arbre binaire de nœuds n1 et n2 est l’ancêtre commun de n1 et n2 situé le plus loin de la racine.

Application de l'ancêtre commun le plus bas (LCA) :

Pour déterminer la distance entre des paires de nœuds dans un arbre : la distance de n1 à n2 peut être calculée comme la distance de la racine à n1, plus la distance de la racine à n2, moins deux fois la distance de la racine à leur plus petit commun. ancêtre.

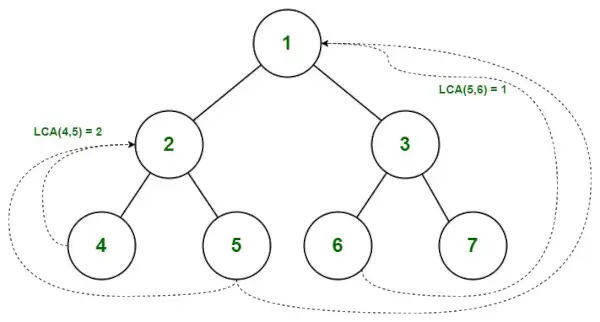
Ancêtre commun le plus bas dans l’arbre binaire

Pratique recommandée Ancêtre commun le plus bas dans un arbre binaire Essayez-le !

Ancêtre commun le plus bas dans un arbre binaire en stockant les chemins de la racine à n1 et de la racine à n2 :

L’idée de cette approche est de stocker le chemin de la racine vers n1 et de la racine vers n2 dans deux structures de données distinctes. Examinez ensuite simultanément les valeurs stockées dans la structure de données et recherchez la première incompatibilité.

Illustration:

Trouver l'ACV de 5 et 6

Chemin de la racine à 5 = { 1, 2, 5 }
Chemin de la racine à 6 = { 1, 3, 6 }

Nous commençons la vérification à partir de l'index 0. Comme les deux valeurs correspondent (pathA[0] = pathB[0] ), nous passons à l’index suivant.

pathA[1] n’est pas égal à pathB[1], il y a une incompatibilité donc nous considérons la valeur précédente.

Donc l'ACV de (5,6) = 1

Suivez les étapes ci-dessous pour résoudre le problème :

Trouvez un chemin de la racine à n1 et stockez-le dans un vecteur ou un tableau.
Trouvez un chemin de la racine à n2 et stockez-le dans un autre vecteur ou tableau.
Parcourez les deux chemins jusqu'à ce que les valeurs des tableaux soient les mêmes. Renvoie l'élément commun juste avant la discordance.

Voici l’implémentation de l’algorithme ci-dessus :

C++

// C++ Program for Lowest Common Ancestor> // in a Binary Tree> // A O(n) solution to find LCA> // of two given values n1 and n2> #include> using> namespace> std;> // A Binary Tree node> struct> Node {> >int> key;> >struct> Node *left, *right;> };> // Utility function creates a new binary tree node with> // given key> Node* newNode(>int> k)> {> >Node* temp =>new> Node;> >temp->clé = k;> >temp->gauche = temp->droite = NULL;> >return> temp;> }> // Finds the path from root node to given root of the tree,> // Stores the path in a vector path[], returns true if path> // exists otherwise false> bool> findPath(Node* root, vector<>int>>& chemin,>int> k)> (root->right && findPath(root->right, path, k)))> >return> true>;> >// If not present in subtree rooted with root, remove> >// root from path[] and return false> >path.pop_back();> >return> false>;> > // Returns LCA if node n1, n2 are present in the given> // binary tree, otherwise return -1> int> findLCA(Node* root,>int> n1,>int> n2)> > // Driver program to test above functions> int> main()> {> >// Let us create the Binary Tree shown in above diagram.> >Node* root = newNode(1);> >root->gauche = nouveauNode(2);> >root->right = newNode(3);> >root->gauche->gauche = newNode(4);> >root->gauche->droite = newNode(5);> >root->droite->gauche = newNode(6);> >root->droite->droite = newNode(7);> >cout <<>'LCA(4, 5) = '> << findLCA(root, 4, 5);> >cout <<>

'
LCA(4, 6) = '>

<< findLCA(root, 4, 6);> >cout <<>

'
LCA(3, 4) = '>

<< findLCA(root, 3, 4);> >cout <<>

'
LCA(2, 4) = '>

<< findLCA(root, 2, 4);> >return> 0;> }>

Java

// Java Program for Lowest Common Ancestor> // in a Binary Tree> // A O(n) solution to find LCA of> // two given values n1 and n2> import> java.util.ArrayList;> import> java.util.List;> // A Binary Tree node> class> Node {> >int> data;> >Node left, right;> >Node(>int> value)> >{> >data = value;> >left = right =>null>;> >}> }> public> class> BT_NoParentPtr_Solution1 {> >Node root;> >private> List path1 =>new> ArrayList();> >private> List path2 =>new> ArrayList();> >// Finds the path from root node to given root of the> >// tree.> >int> findLCA(>int> n1,>int> n2)> >{> >path1.clear();> >path2.clear();> >return> findLCAInternal(root, n1, n2);> >}> >private> int> findLCAInternal(Node root,>int> n1,>int> n2)> >{> >if> (!findPath(root, n1, path1)> >|| !findPath(root, n2, path2)) {> >System.out.println((path1.size()>>0>)> >?>'n1 is present'> >:>'n1 is missing'>);> >System.out.println((path2.size()>>0>)> >?>'n2 is present'> >:>'n2 is missing'>);> >return> ->1>;> >}> >int> i;> >for> (i =>0>

; i   i++) {  // System.out.println(path1.get(i) + ' ' +  // path2.get(i));  if (!path1.get(i).equals(path2.get(i)))  break;  }  return path1.get(i - 1);  }  // Finds the path from root node to given root of the  // tree, Stores the path in a vector path[], returns  // true if path exists otherwise false  private boolean findPath(Node root, int n,  List path)  {  // base case  if (root == null) {  return false;  }  // Store this node . The node will be removed if  // not in path from root to n.  path.add(root.data);  if (root.data == n ||  findPath(root.left, n, path) ||  findPath(root.right, n, path)) {  return true;  }  // If not present in subtree rooted with root,  // remove root from path[] and return false  path.remove(path.size() - 1);  return false;  }  // Driver code  public static void main(String[] args)  {  BT_NoParentPtr_Solution1 tree  = new BT_NoParentPtr_Solution1();  tree.root = new Node(1);  tree.root.left = new Node(2);  tree.root.right = new Node(3);  tree.root.left.left = new Node(4);  tree.root.left.right = new Node(5);  tree.root.right.left = new Node(6);  tree.root.right.right = new Node(7);  System.out.println('LCA(4, 5) = '  + tree.findLCA(4, 5));  System.out.println('LCA(4, 6) = '  + tree.findLCA(4, 6));  System.out.println('LCA(3, 4) = '  + tree.findLCA(3, 4));  System.out.println('LCA(2, 4) = '  + tree.findLCA(2, 4));  } } // This code is contributed by Sreenivasulu Rayanki.>

Python3

# Python Program for Lowest Common Ancestor in a Binary Tree> # O(n) solution to find LCS of two given values n1 and n2> # A binary tree node> class> Node:> ># Constructor to create a new binary node> >def> __init__(>self>, key):> >self>.key>=> key> >self>.left>=> None> >self>.right>=> None> # Finds the path from root node to given root of the tree.> # Stores the path in a list path[], returns true if path> # exists otherwise false> def> findPath(root, path, k):> ># Baes Case> >if> root>is> None>:> >return> False> ># Store this node is path vector. The node will be> ># removed if not in path from root to k> >path.append(root.key)> ># See if the k is same as root's key> >if> root.key>=>=> k:> >return> True> ># Check if k is found in left or right sub-tree> >if> ((root.left !>=> None> and> findPath(root.left, path, k))>or> >(root.right !>=> None> and> findPath(root.right, path, k))):> >return> True> ># If not present in subtree rooted with root, remove> ># root from path and return False> >path.pop()> >return> False> # Returns LCA if node n1 , n2 are present in the given> # binary tree otherwise return -1> def> findLCA(root, n1, n2):> ># To store paths to n1 and n2 fromthe root> >path1>=> []> >path2>=> []> ># Find paths from root to n1 and root to n2.> ># If either n1 or n2 is not present , return -1> >if> (>not> findPath(root, path1, n1)>or> not> findPath(root, path2, n2)):> >return> ->1> ># Compare the paths to get the first different value> >i>=> 0> >while>(i <>len>(path1)>and> i <>len>(path2)):> >if> path1[i] !>=> path2[i]:> >break> >i>+>=> 1> >return> path1[i>->1>]> # Driver program to test above function> if> __name__>=>=> '__main__'>:> > ># Let's create the Binary Tree shown in above diagram> >root>=> Node(>1>)> >root.left>=> Node(>2>)> >root.right>=> Node(>3>)> >root.left.left>=> Node(>4>)> >root.left.right>=> Node(>5>)> >root.right.left>=> Node(>6>)> >root.right.right>=> Node(>7>)> > >print>(>'LCA(4, 5) = %d'> %> (findLCA(root,>4>,>5>,)))> >print>(>'LCA(4, 6) = %d'> %> (findLCA(root,>4>,>6>)))> >print>(>'LCA(3, 4) = %d'> %> (findLCA(root,>3>,>4>)))> >print>(>'LCA(2, 4) = %d'> %> (findLCA(root,>2>,>4>)))> # This code is contributed by Nikhil Kumar Singh(nickzuck_007)>

C#

// C# Program for Lowest Common> // Ancestor in a Binary Tree> // A O(n) solution to find LCA> // of two given values n1 and n2> using> System.Collections;> using> System;> // A Binary Tree node> class> Node {> >public> int> data;> >public> Node left, right;> >public> Node(>int> value)> >{> >data = value;> >left = right =>null>;> >}> }> public> class> BT_NoParentPtr_Solution1 {> >Node root;> >private> ArrayList path1 =>new> ArrayList();> >private> ArrayList path2 =>new> ArrayList();> >// Finds the path from root> >// node to given root of the> >// tree.> >int> findLCA(>int> n1,>int> n2)> >{> >path1.Clear();> >path2.Clear();> >return> findLCAInternal(root, n1, n2);> >}> >private> int> findLCAInternal(Node root,>int> n1,>int> n2)> >{> >if> (!findPath(root, n1, path1)> >|| !findPath(root, n2, path2)) {> >Console.Write((path1.Count>0)> >?>'n1 is present'> >:>'n1 is missing'>);> >Console.Write((path2.Count>0)> >?>'n2 is present'> >:>'n2 is missing'>);> >return> -1;> >}> >int> i;> >for>

(i = 0; i   i++) {  // System.out.println(path1.get(i)  // + ' ' + path2.get(i));  if ((int)path1[i] != (int)path2[i])  break;  }  return (int)path1[i - 1];  }  // Finds the path from root node  // to given root of the tree,  // Stores the path in a vector  // path[], returns true if path  // exists otherwise false  private bool findPath(Node root, int n, ArrayList path)  {  // base case  if (root == null) {  return false;  }  // Store this node . The node  // will be removed if not in  // path from root to n.  path.Add(root.data);  if (root.data == n) {  return true;  }  if (root.left != null  && findPath(root.left, n, path)) {  return true;  }  if (root.right != null  && findPath(root.right, n, path)) {  return true;  }  // If not present in subtree  // rooted with root, remove root  // from path[] and return false  path.RemoveAt(path.Count - 1);  return false;  }  // Driver code  public static void Main(String[] args)  {  BT_NoParentPtr_Solution1 tree  = new BT_NoParentPtr_Solution1();  tree.root = new Node(1);  tree.root.left = new Node(2);  tree.root.right = new Node(3);  tree.root.left.left = new Node(4);  tree.root.left.right = new Node(5);  tree.root.right.left = new Node(6);  tree.root.right.right = new Node(7);  Console.Write('LCA(4, 5) = ' + tree.findLCA(4, 5));  Console.Write('
LCA(4, 6) = '  + tree.findLCA(4, 6));  Console.Write('
LCA(3, 4) = '  + tree.findLCA(3, 4));  Console.Write('
LCA(2, 4) = '  + tree.findLCA(2, 4));  } } // This code is contributed by Rutvik_56>

Javascript

> >// JavaScript Program for Lowest Common> >// Ancestor in a Binary Tree> >// A O(n) solution to find LCA of> >// two given values n1 and n2> > >class Node> >{> >constructor(value) {> >this>.left =>null>;> >this>.right =>null>;> >this>.data = value;> >}> >}> > >let root;> >let path1 = [];> >let path2 = [];> > >// Finds the path from root node to given root of the tree.> >function> findLCA(n1, n2) {> >path1 = [];> >path2 = [];> >return> findLCAInternal(root, n1, n2);> >}> > >function> findLCAInternal(root, n1, n2) {> > >if> (!findPath(root, n1, path1) || !findPath(root, n2, path2))> >{> >document.write((path1.length>0) ?> >'n1 is present'> :>'n1 is missing'>);> >document.write((path2.length>0) ?> >'n2 is present'> :>'n2 is missing'>);> >return> -1;> >}> > >let i;> >for>

(i = 0; i     // System.out.println(path1.get(i) + ' ' + path2.get(i));  if (path1[i] != path2[i])  break;  }    return path1[i-1];  }    // Finds the path from root node to   // given root of the tree, Stores the  // path in a vector path[], returns true  // if path exists otherwise false  function findPath(root, n, path)  {  // base case  if (root == null) {  return false;  }    // Store this node . The node will be removed if  // not in path from root to n.  path.push(root.data);    if (root.data == n) {  return true;  }    if (root.left != null && findPath(root.left, n, path)) {  return true;  }    if (root.right != null && findPath(root.right, n, path)) {  return true;  }    // If not present in subtree rooted with root,   // remove root from  // path[] and return false  path.pop();    return false;  }    root = new Node(1);  root.left = new Node(2);  root.right = new Node(3);  root.left.left = new Node(4);  root.left.right = new Node(5);  root.right.left = new Node(6);  root.right.right = new Node(7);  document.write('LCA(4, 5) = ' + findLCA(4,5) + '');  document.write('LCA(4, 6) = ' + findLCA(4,6) + '');  document.write('LCA(3, 4) = ' + findLCA(3,4) + '');  document.write('LCA(2, 4) = ' + findLCA(2,4));>

Sortir

LCA(4, 5) = 2 LCA(4, 6) = 1 LCA(3, 4) = 1 LCA(2, 4) = 2>

Complexité temporelle : SUR). L'arbre est parcouru deux fois, puis les tableaux de chemins sont comparés.
Espace auxiliaire : SUR). Espace supplémentaire pour path1 et path2.

Ancêtre commun le plus bas dans un arbre binaire par traversée unique :

L'idée est de parcourir l'arbre en partant de la racine. Si l'une des clés données (n1 et n2) correspond à la racine, alors la racine est LCA (en supposant que les deux clés sont présentes). Si la racine ne correspond à aucune des clés, nous répétons pour les sous-arbres gauche et droit.

Le nœud qui a une clé présente dans son sous-arbre de gauche et l'autre clé présente dans le sous-arbre de droite est le LCA.

Si les deux clés se trouvent dans le sous-arbre de gauche, alors le sous-arbre de gauche a également LCA,

Sinon, LCA se trouve dans le sous-arbre de droite.

Illustration:

Trouver l'ACV de 5 et 6

Racine pointe vers le nœud avec la valeur 1, car sa valeur ne correspond pas à { 5, 6 }. Nous recherchons la clé dans le sous-arbre gauche et le sous-arbre droit.

Sous-arbre gauche :

New Root = { 2 } ≠ 5 ou 6, nous allons donc continuer notre récursion

New Root = { 4 } , le sous-arbre gauche et droit est nul, nous renverrons NULL pour cet appel

New Root = { 5 } , la valeur correspond à 5 et renverra donc le nœud avec la valeur 5

L'appel de fonction pour root avec la valeur 2 renverra une valeur de 5

Sous-arbre droit :

Root = { 3 } ≠ 5 ou 6 donc nous continuons notre récursion

Root = { 6 } = 5 ou 6 , nous renverrons ce nœud avec la valeur 6

Root = { 7 } ≠ 5 ou 6, nous renverrons NULL

Ainsi, l'appel de fonction pour root avec la valeur 3 renverra le nœud avec la valeur 6

Comme le sous-arbre gauche et le sous-arbre droit du nœud avec la valeur 1 ne sont pas NULL, donc 1 est la LCA.

Suivez les étapes ci-dessous pour résoudre le problème :

Nous transmettons la racine à une fonction d'assistance et vérifions si la valeur de la racine correspond à l'un des n1 et n2.
- Si OUI, renvoie la racine
- sinon appel récursif sur le sous-arbre gauche et droit
Fondamentalement, nous effectuons un parcours de pré-commande, dans un premier temps nous vérifions si la racine->valeur correspond à n1 ou n2. Traversez ensuite le sous-arbre gauche et droit.
S'il existe une racine qui renvoie une valeur NULL et une autre valeur NON-NULL, nous renverrons la valeur NON-NULL correspondante pour ce nœud.
Le nœud qui renvoie les deux valeurs NON NULL pour les sous-arbres gauche et droit est notre ancêtre commun le plus bas.

Vous trouverez ci-dessous la mise en œuvre de l’approche ci-dessus.

C++

/* C++ Program to find LCA of n1 and n2 using one traversal> >* of Binary Tree */> #include> using> namespace> std;> // A Binary Tree Node> struct> Node {> >struct> Node *left, *right;> >int> key;> };> // Utility function to create a new tree Node> Node* newNode(>int> key)> {> >Node* temp =>new> Node;> >temp->clé = clé;> >temp->gauche = temp->droite = NULL;> >return> temp;> }> // This function returns pointer to LCA of two given values> // n1 and n2. This function assumes that n1 and n2 are> // present in Binary Tree> struct> Node* findLCA(>struct> Node* root,>int> n1,>int> n2)> > >// Base case> >if> (root == NULL)> >return> NULL;> >// If either n1 or n2 matches with root's key, report> >// the presence by returning root (Note that if a key is> >// ancestor of other, then the ancestor key becomes LCA> >if> (root->clé == n1> // Driver program to test above functions> int> main()> {> >// Let us create binary tree given in the above example> >Node* root = newNode(1);> >root->gauche = nouveauNode(2);> >root->right = newNode(3);> >root->gauche->gauche = newNode(4);> >root->gauche->droite = newNode(5);> >root->droite->gauche = newNode(6);> >root->droite->droite = newNode(7);> >cout <<>'LCA(4, 5) = '>

  cout << '
LCA(4, 6) = '   cout << '
LCA(3, 4) = '   cout << '
LCA(2, 4) = '   return 0; } // This code is contributed by Aditya Kumar (adityakumar129)>

C

// C Program to find LCA of n1 and n2 using one traversalof> // Binary Tree> #include> #include> // A Binary Tree Node> typedef> struct> Node {> >struct> Node *left, *right;> >int> key;> } Node;> // Utility function to create a new tree Node> Node* newNode(>int> key)> {> >Node* temp = (Node*)>malloc>(>sizeof>(Node));> >temp->clé = clé;> >temp->gauche = temp->droite = NULL;> >return> temp;> }> // This function returns pointer to LCA of two given values> // n1 and n2. This function assumes that n1 and n2 are> // present in Binary Tree> Node* findLCA(Node* root,>int> n1,>int> n2)> > >// Base case> >if> (root == NULL)> >return> NULL;> >// If either n1 or n2 matches with root's key, report> >// the presence by returning root (Note that if a key is> >// ancestor of other, then the ancestor key becomes LCA> >if> (root->clé == n1> // Driver program to test above functions> int> main()> {> >// Let us create binary tree given in the above example> >Node* root = newNode(1);> >root->gauche = nouveauNode(2);> >root->right = newNode(3);> >root->gauche->gauche = newNode(4);> >root->gauche->droite = newNode(5);> >root->droite->gauche = newNode(6);> >root->droite->droite = newNode(7);> >printf>(>'LCA(4, 5) = %d'>, findLCA(root, 4, 5)->clé);> >printf>(>

'
LCA(4, 6) = %d'>

, findLCA(root, 4, 6)->clé);> >printf>(>

'
LCA(3, 4) = %d'>

, findLCA(root, 3, 4)->clé);> >printf>(>

'
LCA(2, 4) = %d'>

, findLCA(root, 2, 4)->clé);> >return> 0;> }> // This code is contributed by Aditya Kumar (adityakumar129)>

Java

// Java implementation to find lowest common ancestor of> // n1 and n2 using one traversal of binary tree> /* Class containing left and right child of current> >node and key value*/> class> Node {> >int> data;> >Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> public> class> BinaryTree {> >// Root of the Binary Tree> >Node root;> >Node findLCA(>int> n1,>int> n2)> >{> >return> findLCA(root, n1, n2);> >}> >// This function returns pointer to LCA of two given> >// values n1 and n2. This function assumes that n1 and> >// n2 are present in Binary Tree> >Node findLCA(Node node,>int> n1,>int> n2)> >> >// Base case> >if> (node ==>null>)> >return> null>;> >// If either n1 or n2 matches with root's key,> >// report the presence by returning root (Note that> >// if a key is ancestor of other, then the ancestor> >// key becomes LCA> >if> (node.data == n1> >/* Driver program to test above functions */> >public> static> void> main(String args[])> >{> >BinaryTree tree =>new> BinaryTree();> >tree.root =>new> Node(>1>);> >tree.root.left =>new> Node(>2>);> >tree.root.right =>new> Node(>3>);> >tree.root.left.left =>new> Node(>4>);> >tree.root.left.right =>new> Node(>5>);> >tree.root.right.left =>new> Node(>6>);> >tree.root.right.right =>new> Node(>7>);> >System.out.println(>'LCA(4, 5) = '> >+ tree.findLCA(>4>,>5>).data);> >System.out.println(>'LCA(4, 6) = '> >+ tree.findLCA(>4>,>6>).data);> >System.out.println(>'LCA(3, 4) = '> >+ tree.findLCA(>3>,>4>).data);> >System.out.println(>'LCA(2, 4) = '> >+ tree.findLCA(>2>,>4>).data);> >}> }>

Python3

# Python program to find LCA of n1 and n2 using one> # traversal of Binary tree> # A binary tree node> class> Node:> ># Constructor to create a new tree node> >def> __init__(>self>, key):> >self>.key>=> key> >self>.left>=> None> >self>.right>=> None> # This function returns pointer to LCA of two given> # values n1 and n2> # This function assumes that n1 and n2 are present in> # Binary Tree> def> findLCA(root, n1, n2):> ># Base Case> >if> root>is> None>:> >return> None> ># If either n1 or n2 matches with root's key, report> ># the presence by returning root (Note that if a key is> ># ancestor of other, then the ancestor key becomes LCA> >if> root.key>=>=> n1>or> root.key>=>=> n2:> >return> root> ># Look for keys in left and right subtrees> >left_lca>=> findLCA(root.left, n1, n2)> >right_lca>=> findLCA(root.right, n1, n2)> ># If both of the above calls return Non-NULL, then one key> ># is present in once subtree and other is present in other,> ># So this node is the LCA> >if> left_lca>and> right_lca:> >return> root> ># Otherwise check if left subtree or right subtree is LCA> >return> left_lca>if> left_lca>is> not> None> else> right_lca> # Driver code> if> __name__>=>=> '__main__'>:> > ># Let us create a binary tree given in the above example> >root>=> Node(>1>)> >root.left>=> Node(>2>)> >root.right>=> Node(>3>)> >root.left.left>=> Node(>4>)> >root.left.right>=> Node(>5>)> >root.right.left>=> Node(>6>)> >root.right.right>=> Node(>7>)> >print>(>'LCA(4, 5) = '>, findLCA(root,>4>,>5>).key)> >print>(>'LCA(4, 6) = '>, findLCA(root,>4>,>6>).key)> >print>(>'LCA(3, 4) = '>, findLCA(root,>3>,>4>).key)> >print>(>'LCA(2, 4) = '>, findLCA(root,>2>,>4>).key)> # This code is contributed by Nikhil Kumar Singh(nickzuck_007)>

C#

// C# implementation to find lowest common> // ancestor of n1 and n2 using one traversal> // of binary tree> using> System;> // Class containing left and right> // child of current node and key value> public> class> Node {> >public> int> data;> >public> Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> class> BinaryTree {> >// Root of the Binary Tree> >Node root;> >Node findLCA(>int> n1,>int> n2)> >{> >return> findLCA(root, n1, n2);> >}> >// This function returns pointer to LCA> >// of two given values n1 and n2. This> >// function assumes that n1 and n2 are> >// present in Binary Tree> >Node findLCA(Node node,>int> n1,>int> n2)> > node.data == n2)> >return> node;> >// Look for keys in left and right subtrees> >Node left_lca = findLCA(node.left, n1, n2);> >Node right_lca = findLCA(node.right, n1, n2);> >// If both of the above calls return Non-NULL,> >// then one key is present in once subtree> >// and other is present in other, So this> >// node is the LCA> >if> (left_lca !=>null> && right_lca !=>null>)> >return> node;> >// Otherwise check if left subtree or> >// right subtree is LCA> >return> (left_lca !=>null>) ? left_lca : right_lca;> >> >// Driver code> >public> static> void> Main(>string>[] args)> >{> >BinaryTree tree =>new> BinaryTree();> >tree.root =>new> Node(1);> >tree.root.left =>new> Node(2);> >tree.root.right =>new> Node(3);> >tree.root.left.left =>new> Node(4);> >tree.root.left.right =>new> Node(5);> >tree.root.right.left =>new> Node(6);> >tree.root.right.right =>new> Node(7);> >Console.WriteLine(>'LCA(4, 5) = '> >+ tree.findLCA(4, 5).data);> >Console.WriteLine(>'LCA(4, 6) = '> >+ tree.findLCA(4, 6).data);> >Console.WriteLine(>'LCA(3, 4) = '> >+ tree.findLCA(3, 4).data);> >Console.WriteLine(>'LCA(2, 4) = '> >+ tree.findLCA(2, 4).data);> >}> }> // This code is contributed by pratham76>

Javascript

> >// JavaScript implementation to find> >// lowest common ancestor of> >// n1 and n2 using one traversal of binary tree> > >class Node> >{> >constructor(item) {> >this>.left =>null>;> >this>.right =>null>;> >this>.data = item;> >}> >}> > >//Root of the Binary Tree> >let root;> > >function> findlCA(n1, n2)> >{> >return> findLCA(root, n1, n2);> >}> > >// This function returns pointer to LCA of two given> >// values n1 and n2. This function assumes that n1 and> >// n2 are present in Binary Tree> >function> findLCA(node, n1, n2)> >> > >root =>new> Node(1);> >root.left =>new> Node(2);> >root.right =>new> Node(3);> >root.left.left =>new> Node(4);> >root.left.right =>new> Node(5);> >root.right.left =>new> Node(6);> >root.right.right =>new> Node(7);> >document.write(>'LCA(4, 5) = '> +> >findlCA(4, 5).data +>''>);> >document.write(>'LCA(4, 6) = '> +> >findlCA(4, 6).data +>''>);> >document.write(>'LCA(3, 4) = '> +> >findlCA(3, 4).data +>''>);> >document.write(>'LCA(2, 4) = '> +> >findlCA(2, 4).data +>''>);> > >

Sortir

LCA(4, 5) = 2 LCA(4, 6) = 1 LCA(3, 4) = 1 LCA(2, 4) = 2>

Complexité temporelle : O(N) car la méthode effectue une simple traversée d’arbre de bas en haut.
Espace auxiliaire : O(H), où H est la hauteur de l'arbre.

Note: La méthode ci-dessus suppose que les clés sont présentes dans l'arbre binaire . Si une clé est présente et l'autre est absente, alors elle renvoie la clé actuelle sous forme de LCA (idéalement, elle aurait dû renvoyer NULL). Nous pouvons étendre cette méthode pour traiter tous les cas en vérifiant d'abord si n1 et n2 sont présents dans l'arborescence, puis en trouvant l'ACV de n1 et n2. Pour vérifier si le nœud est présent ou non dans l'arborescence binaire, parcourez l'arborescence pour les nœuds n1 et n2 séparément.

C++

/* C++ program to find LCA of n1 and n2 using one traversal> >of Binary Tree. It handles all cases even when n1 or n2> >is not there in Binary Tree */> #include> using> namespace> std;> // A Binary Tree Node> struct> Node {> >struct> Node *left, *right;> >int> key;> };> // Utility function to create a new tree Node> Node* newNode(>int> key)> {> >Node* temp =>new> Node;> >temp->clé = clé;> >temp->gauche = temp->droite = NULL;> >return> temp;> }> // This function returns pointer to LCA of two given> // valuesn1 and n2.> struct> Node* findLCAUtil(>struct> Node* root,>int> n1,>int> n2)> > // Returns true if key k is present in tree rooted with root> bool> find(Node* root,>int> k)> find(root->à droite, k))> >return> true>;> >// Else return false> >return> false>;> > // This function returns LCA of n1 and n2 only if both n1> // and n2 are present in tree, otherwise returns NULL;> Node* findLCA(Node* root,>int> n1,>int> n2)> {> >// Return LCA only if both n1 and n2 are present in tree> >if> (find(root, n1) and find(root, n2))> >return> findLCAUtil(root, n1, n2);> >// Else return NULL> >return> NULL;> }> // Driver program to test above functions> int> main()> {> >// Let us create a binary tree given in the above> >// example> >Node* root = newNode(1);> >root->gauche = nouveauNode(2);> >root->right = newNode(3);> >root->gauche->gauche = newNode(4);> >root->gauche->droite = newNode(5);> >root->droite->gauche = newNode(6);> >root->droite->droite = newNode(7);> >Node* lca = findLCA(root, 4, 5);> >if> (lca != NULL)> >cout <<>'LCA(4, 5) = '>

  else  cout << 'Keys are not present ';  lca = findLCA(root, 4, 10);  if (lca != NULL)  cout << '
LCA(4, 10) = '   else  cout << '
Keys are not present ';  return 0; } // This code is contributed by Kshitij Dwivedi // (kshitijdwivedi28)>

Java

// Java implementation to find lowest common ancestor of> // n1 and n2 using one traversal of binary tree> // It also handles cases even when n1 and n2 are not there> // in Tree> /* Class containing left and right child of current node and> >* key */> class> Node {> >int> data;> >Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> public> class> BinaryTree {> >// Root of the Binary Tree> >Node root;> >static> boolean> v1 =>false>, v2 =>false>;> >// This function returns pointer to LCA of two given> >// values n1 and n2.> >// v1 is set as true by this function if n1 is found> >// v2 is set as true by this function if n2 is found> >Node findLCAUtil(Node node,>int> n1,>int> n2)> >{> >// Base case> >if> (node ==>null>)> >return> null>;> >// Store result in temp, in case of key match so> >// that we can search for other key also.> >Node temp =>null>;> >// If either n1 or n2 matches with root's key,> >// report the presence by setting v1 or v2 as true> >// and return root (Note that if a key is ancestor> >// of other, then the ancestor key becomes LCA)> >if> (node.data == n1) {> >v1 =>true>;> >temp = node;> >}> >if> (node.data == n2) {> >v2 =>true>;> >temp = node;> >}> >// Look for keys in left and right subtrees> >Node left_lca = findLCAUtil(node.left, n1, n2);> >Node right_lca = findLCAUtil(node.right, n1, n2);> >if> (temp !=>null>)> >return> temp;> >// If both of the above calls return Non-NULL, then> >// one key is present in once subtree and other is> >// present in other, So this node is the LCA> >if> (left_lca !=>null> && right_lca !=>null>)> >return> node;> >// Otherwise check if left subtree or right subtree> >// is LCA> >return> (left_lca !=>null>) ? left_lca : right_lca;> >}> >// Finds lca of n1 and n2 under the subtree rooted with> >// 'node'> >Node findLCA(>int> n1,>int> n2)> >{> >// Initialize n1 and n2 as not visited> >v1 =>false>;> >v2 =>false>;> >// Find lca of n1 and n2 using the technique> >// discussed above> >Node lca = findLCAUtil(root, n1, n2);> >// Return LCA only if both n1 and n2 are present in> >// tree> >if> (v1 && v2)> >return> lca;> >// Else return NULL> >return> null>;> >}> >/* Driver program to test above functions */> >public> static> void> main(String args[])> >{> >BinaryTree tree =>new> BinaryTree();> >tree.root =>new> Node(>1>);> >tree.root.left =>new> Node(>2>);> >tree.root.right =>new> Node(>3>);> >tree.root.left.left =>new> Node(>4>);> >tree.root.left.right =>new> Node(>5>);> >tree.root.right.left =>new> Node(>6>);> >tree.root.right.right =>new> Node(>7>);> >Node lca = tree.findLCA(>4>,>5>);> >if> (lca !=>null>)> >System.out.println(>'LCA(4, 5) = '> + lca.data);> >else> >System.out.println(>'Keys are not present'>);> >lca = tree.findLCA(>4>,>10>);> >if> (lca !=>null>)> >System.out.println(>'LCA(4, 10) = '> + lca.data);> >else> >System.out.println(>'Keys are not present'>);> >}> }>

Python3

''' Program to find LCA of n1 and n2 using one traversal of> >Binary tree> It handles all cases even when n1 or n2 is not there in tree> '''> # A binary tree node> class> Node:> ># Constructor to create a new node> >def> __init__(>self>, key):> >self>.key>=> key> >self>.left>=> None> >self>.right>=> None> # This function return pointer to LCA of two given values> # n1 and n2> # v1 is set as true by this function if n1 is found> # v2 is set as true by this function if n2 is found> def> findLCAUtil(root, n1, n2, v):> ># Base Case> >if> root>is> None>:> >return> None> ># IF either n1 or n2 matches ith root's key, report> ># the presence by setting v1 or v2 as true and return> ># root (Note that if a key is ancestor of other, then> ># the ancestor key becomes LCA)> >if> root.key>=>=> n1:> >v[>0>]>=> True> >return> root> >if> root.key>=>=> n2:> >v[>1>]>=> True> >return> root> ># Look for keys in left and right subtree> >left_lca>=> findLCAUtil(root.left, n1, n2, v)> >right_lca>=> findLCAUtil(root.right, n1, n2, v)> ># If both of the above calls return Non-NULL, then one key> ># is present in once subtree and other is present in other,> ># So this node is the LCA> >if> left_lca>and> right_lca:> >return> root> ># Otherwise check if left subtree or right subtree is LCA> >return> left_lca>if> left_lca>is> not> None> else> right_lca> def> find(root, k):> ># Base Case> >if> root>is> None>:> >return> False> ># If key is present at root, or if left subtree or right> ># subtree , return true> >if> (root.key>=>=> k>or> find(root.left, k)>or> >find(root.right, k)):> >return> True> ># Else return false> >return> False> # This function returns LCA of n1 and n2 on value if both> # n1 and n2 are present in tree, otherwise returns None> def> findLCA(root, n1, n2):> ># Initialize n1 and n2 as not visited> >v>=> [>False>,>False>]> ># Find lca of n1 and n2 using the technique discussed above> >lca>=> findLCAUtil(root, n1, n2, v)> ># Returns LCA only if both n1 and n2 are present in tree> >if> (v[>0>]>and> v[>1>]>or> v[>0>]>and> find(lca, n2)>or> v[>1>]>and> >find(lca, n1)):> >return> lca> ># Else return None> >return> None> # Driver program to test above function> root>=> Node(>1>)> root.left>=> Node(>2>)> root.right>=> Node(>3>)> root.left.left>=> Node(>4>)> root.left.right>=> Node(>5>)> root.right.left>=> Node(>6>)> root.right.right>=> Node(>7>)> lca>=> findLCA(root,>4>,>5>)> if> lca>is> not> None>:> >print>(>'LCA(4, 5) = '>, lca.key)> else>:> >print>(>'Keys are not present'>)> lca>=> findLCA(root,>4>,>10>)> if> lca>is> not> None>:> >print>(>'LCA(4,10) = '>, lca.key)> else>:> >print>(>'Keys are not present'>)> # This code is contributed by Nikhil Kumar Singh(nickzuck_007)>

C#

using> System;> // c# implementation to find lowest common ancestor of> // n1 and n2 using one traversal of binary tree> // It also handles cases even when n1 and n2 are not there> // in Tree> /* Class containing left and right child of current node and> >* key */> public> class> Node {> >public> int> data;> >public> Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> public> class> BinaryTree {> >// Root of the Binary Tree> >public> Node root;> >public> static> bool> v1 =>false>, v2 =>false>;> >// This function returns pointer to LCA of two given> >// values n1 and n2.> >// v1 is set as true by this function if n1 is found> >// v2 is set as true by this function if n2 is found> >public> virtual> Node findLCAUtil(Node node,>int> n1,> >int> n2)> >{> >// Base case> >if> (node ==>null>) {> >return> null>;> >}> >// Store result in temp, in case of key match so> >// that we can search for other key also.> >Node temp =>null>;> >// If either n1 or n2 matches with root's key,> >// report the presence by setting v1 or v2 as true> >// and return root (Note that if a key is ancestor> >// of other, then the ancestor key becomes LCA)> >if> (node.data == n1) {> >v1 =>true>;> >temp = node;> >}> >if> (node.data == n2) {> >v2 =>true>;> >temp = node;> >}> >// Look for keys in left and right subtrees> >Node left_lca = findLCAUtil(node.left, n1, n2);> >Node right_lca = findLCAUtil(node.right, n1, n2);> >if> (temp !=>null>) {> >return> temp;> >}> >// If both of the above calls return Non-NULL, then> >// one key is present in once subtree and other is> >// present in other, So this node is the LCA> >if> (left_lca !=>null> && right_lca !=>null>) {> >return> node;> >}> >// Otherwise check if left subtree or right subtree> >// is LCA> >return> (left_lca !=>null>) ? left_lca : right_lca;> >}> >// Finds lca of n1 and n2 under the subtree rooted with> >// 'node'> >public> virtual> Node findLCA(>int> n1,>int> n2)> >{> >// Initialize n1 and n2 as not visited> >v1 =>false>;> >v2 =>false>;> >// Find lca of n1 and n2 using the technique> >// discussed above> >Node lca = findLCAUtil(root, n1, n2);> >// Return LCA only if both n1 and n2 are present in> >// tree> >if> (v1 && v2) {> >return> lca;> >}> >// Else return NULL> >return> null>;> >}> >/* Driver program to test above functions */> >public> static> void> Main(>string>[] args)> >{> >BinaryTree tree =>new> BinaryTree();> >tree.root =>new> Node(1);> >tree.root.left =>new> Node(2);> >tree.root.right =>new> Node(3);> >tree.root.left.left =>new> Node(4);> >tree.root.left.right =>new> Node(5);> >tree.root.right.left =>new> Node(6);> >tree.root.right.right =>new> Node(7);> >Node lca = tree.findLCA(4, 5);> >if> (lca !=>null>) {> >Console.WriteLine(>'LCA(4, 5) = '> + lca.data);> >}> >else> {> >Console.WriteLine(>'Keys are not present'>);> >}> >lca = tree.findLCA(4, 10);> >if> (lca !=>null>) {> >Console.WriteLine(>'LCA(4, 10) = '> + lca.data);> >}> >else> {> >Console.WriteLine(>'Keys are not present'>);> >}> >}> }> // This code is contributed by Shrikant13>

Javascript

> // JavaScript implementation to find lowest> // common ancestor of n1 and n2 using one> // traversal of binary tree. It also handles> // cases even when n1 and n2 are not there in Tree> // Class containing left and right child> // of current node and key> class Node> {> >constructor(item)> >{> >this>.data = item;> >this>.left =>null>;> >this>.right =>null>;> >}> }> class BinaryTree{> > // Root of the Binary Tree> constructor()> {> >this>.root =>null>;> >this>.v1 =>false>;> >this>.v2 =>false>;> }> // This function returns pointer to LCA> // of two given values n1 and n2.> // v1 is set as true by this function> // if n1 is found> // v2 is set as true by this function> // if n2 is found> findLCAUtil(node, n1, n2)> {> > >// Base case> >if> (node ==>null>)> >{> >return> null>;> >}> > >// Store result in temp, in case of> >// key match so that we can search> >// for other key also.> >var> temp =>null>;> > >// If either n1 or n2 matches with root's key,> >// report the presence by setting v1 or v2 as> >// true and return root (Note that if a key> >// is ancestor of other, then the ancestor> >// key becomes LCA)> >if> (node.data == n1)> >{> >this>.v1 =>true>;> >temp = node;> >}> >if> (node.data == n2)> >{> >this>.v2 =>true>;> >temp = node;> >}> > >// Look for keys in left and right subtrees> >var> left_lca =>this>.findLCAUtil(node.left, n1, n2);> >var> right_lca =>this>.findLCAUtil(node.right, n1, n2);> > >if> (temp !=>null>)> >{> >return> temp;> >}> > >// If both of the above calls return Non-NULL,> >// then one key is present in once subtree and> >// other is present in other, So this node is the LCA> >if> (left_lca !=>null> && right_lca !=>null>)> >{> >return> node;> >}> > >// Otherwise check if left subtree or> >// right subtree is LCA> >return> left_lca !=>null> ? left_lca : right_lca;> }> // Finds lca of n1 and n2 under the> // subtree rooted with 'node'> findLCA(n1, n2)> {> > >// Initialize n1 and n2 as not visited> >this>.v1 =>false>;> >this>.v2 =>false>;> > >// Find lca of n1 and n2 using the> >// technique discussed above> >var> lca =>this>.findLCAUtil(>this>.root, n1, n2);> > >// Return LCA only if both n1 and n2> >// are present in tree> >if> (>this>.v1 &&>this>.v2)> >{> >return> lca;> >}> > >// Else return NULL> >return> null>;> }> }> // Driver code> var> tree =>new> BinaryTree();> tree.root =>new> Node(1);> tree.root.left =>new> Node(2);> tree.root.right =>new> Node(3);> tree.root.left.left =>new> Node(4);> tree.root.left.right =>new> Node(5);> tree.root.right.left =>new> Node(6);> tree.root.right.right =>new> Node(7);> var> lca = tree.findLCA(4, 5);> if> (lca !=>null>)> {> >document.write(>'LCA(4, 5) = '> +> >lca.data +>' '>);> }>else> {> >document.write(>'Keys are not present'> +>' '>);> }> lca = tree.findLCA(4, 10);> if> (lca !=>null>)> {> >document.write(>'LCA(4, 10) = '> +> >lca.data +>' '>);> }> else> {> >document.write(>'Keys are not present'> +>' '>);> }> // This code is contributed by rdtank> >

Sortir

LCA(4, 5) = 2 Keys are not present>

Complexité temporelle : O(N) car la méthode effectue une simple traversée d’arbre de bas en haut.
Espace auxiliaire : O(H), où h est la hauteur de l'arbre.

Utilisation d'une structure de données auxiliaire (table de hachage) :

The basic idea behind the 'Using an auxiliary data structure' approach for finding the lowest common ancestor of two nodes in a binary tree is to use a hash table or a map to store the parent pointers of each node. Once we have the parent pointers, we can traverse up from the first node and add all its ancestors to a set or a list. Then we can traverse up from the second node and check if each ancestor is already in the set or the list. The first ancestor that is already in the set or the list is the lowest common ancestor.>

Suivez les étapes pour mettre en œuvre l’approche ci-dessus :

Créez une table de hachage ou une carte pour stocker les pointeurs parents de chaque nœud dans l'arborescence binaire.
Parcourez l'arborescence binaire et remplissez la table de hachage ou la carte avec les pointeurs parents pour chaque nœud.
En partant du premier nœud, parcourez l'arborescence et ajoutez chaque ancêtre à un ensemble ou à une liste.
En partant du deuxième nœud, parcourez l'arborescence et vérifiez si chaque ancêtre est déjà dans l'ensemble ou la liste. Le premier ancêtre déjà présent dans l’ensemble ou la liste est l’ancêtre commun le plus bas.
Si aucun ancêtre commun n'est trouvé, renvoie null ou toute autre valeur indiquant l'absence d'ancêtre commun.

Vous trouverez ci-dessous la mise en œuvre de l'approche ci-dessus :

C++

// C++ code to implement above approach> #include> #include> #include> #include> using> namespace> std;> // Definition of a binary tree node> struct> Node {> >int> data;> >Node* left;> >Node* right;> };> // Function to create a new binary tree node> Node* newNode(>int> data)> {> >Node* node =>new> Node;> >node->données = données ;> >node->gauche = NULL;> >node->droite = NULL;> >return> (node);> }> // Function to build a hash table or a map of parent> // pointers for each node in the tree> unordered_map buildParentMap(Node* root)> {> >unordered_map parentMap;> >parentMap[root] = NULL;> >vector queue = { root };> >while> (!queue.empty()) {> >Node* node = queue.front();> >queue.erase(queue.begin());> >if> (node->gauche) {> >parentMap[node->gauche] = nœud;> >queue.push_back(node->à gauche);> >}> >if> (node->à droite) {> >parentMap[node->droite] = nœud;> >queue.push_back(node->à droite);> >}> >}> >return> parentMap;> }> // Function to find the lowest common ancestor of two nodes> // using an auxiliary data structure> int> findLCA(Node* root,>int> n1,>int> n2)> {> >// Build a hash table or a map of parent pointers for> >// each node in the tree> >unordered_map parentMap> >= buildParentMap(root);> >// Find the nodes with values n1 and n2> >Node* p = NULL;> >Node* q = NULL;> >vector queue = { root };> >while> (!queue.empty()) {> >Node* node = queue.front();> >queue.erase(queue.begin());> >if> (node->données == n1) {> >p = node;> >}> >if> (node->données == n2) {> >q = node;> >}> >if> (node->gauche) {> >queue.push_back(node->à gauche);> >}> >if> (node->à droite) {> >queue.push_back(node->à droite);> >}> >}> >// Add all the ancestors of the first node to a set or a> >// list> >set ancestors;> >while> (p) {> >ancestors.insert(p);> >p = parentMap[p];> >}> >// Traverse up from the second node and check if each> >// ancestor is already in the set or the list> >while> (q) {> >if> (ancestors.find(q) != ancestors.end()) {> >return> q> >->données;>// The first ancestor that is> >// already in the set or the list is> >// the lowest common ancestor> >}> >q = parentMap[q];> >}> >return> -1;>// No common ancestor found> }> // Driver code> int> main()> {> >Node* root = newNode(1);> >root->gauche = nouveauNode(2);> >root->right = newNode(3);> >root->gauche->gauche = newNode(4);> >root->gauche->droite = newNode(5);> >root->droite->gauche = newNode(6);> >root->droite->droite = newNode(7);> >cout <<>'LCA(4, 5) = '> << findLCA(root, 4, 5) << endl;> >cout <<>'LCA(4, 6) = '> << findLCA(root, 4, 6) << endl;> >cout <<>'LCA(3,4) = '> << findLCA(root, 3, 4) << endl;> >cout <<>'LCA(2, 4) = '> << findLCA(root, 2, 4) << endl;> >return> 0;> }> // This code is contributed by Veerendra_Singh_Rajpoot>

Java

import> java.util.*;> // Definition of a binary tree node> class> Node {> >int> data;> >Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> class> Main {> >// Function to build a hash table or a map of parent> >// pointers for each node in the tree> >static> Map buildParentMap(Node root)> >{> >Map parentMap =>new> HashMap();> >parentMap.put(root,>null>);> >Queue queue =>new> LinkedList();> >queue.add(root);> >while> (!queue.isEmpty()) {> >Node node = queue.poll();> >if> (node.left !=>null>) {> >parentMap.put(node.left, node);> >queue.add(node.left);> >}> >if> (node.right !=>null>) {> >parentMap.put(node.right, node);> >queue.add(node.right);> >}> >}> >return> parentMap;> >}> >// Function to find the lowest common ancestor of two> >// nodes using an auxiliary data structure> >static> int> findLCA(Node root,>int> n1,>int> n2)> >{> >// Build a hash table or a map of parent pointers> >// for each node in the tree> >Map parentMap = buildParentMap(root);> >// Find the nodes with values n1 and n2> >Node p =>null>, q =>null>;> >Queue queue =>new> LinkedList();> >queue.add(root);> >while> (!queue.isEmpty()) {> >Node node = queue.poll();> >if> (node.data == n1) {> >p = node;> >}> >if> (node.data == n2) {> >q = node;> >}> >if> (node.left !=>null>) {> >queue.add(node.left);> >}> >if> (node.right !=>null>) {> >queue.add(node.right);> >}> >}> >// Add all the ancestors of the first node to a set> >// or a list> >Set ancestors =>new> HashSet();> >while> (p !=>null>) {> >ancestors.add(p);> >p = parentMap.get(p);> >}> >// Traverse up from the second node and check if> >// each ancestor is already in the set or the list> >while> (q !=>null>) {> >if> (ancestors.contains(q)) {> >return> q.data;> >}> >q = parentMap.get(q);> >}> >return> ->1>;>// No common ancestor found> >}> >public> static> void> main(String[] args)> >{> >Node root =>new> Node(>1>);> >root.left =>new> Node(>2>);> >root.right =>new> Node(>3>);> >root.left.left =>new> Node(>4>);> >root.left.right =>new> Node(>5>);> >root.right.left =>new> Node(>6>);> >root.right.right =>new> Node(>7>);> >System.out.println(>'LCA(4, 5) = '> >+ findLCA(root,>4>,>5>));> >System.out.println(>'LCA(4, 6) = '> >+ findLCA(root,>4>,>6>));> >System.out.println(>'LCA(3, 4) = '> >+ findLCA(root,>3>,>4>));> >System.out.println(>'LCA(3, 4) = '> >+ findLCA(root,>2>,>4>));> >}> }>

Python3

from> collections>import> deque> # Definition of a binary tree node> class> Node:> >def> __init__(>self>, data):> >self>.data>=> data> >self>.left>=> None> >self>.right>=> None> # Function to build a hash table or a map of parent> # pointers for each node in the tree> def> buildParentMap(root):> >parentMap>=> {}> >parentMap[root]>=> None> >queue>=> deque([root])> >while> queue:> >node>=> queue.popleft()> >if> node.left:> >parentMap[node.left]>=> node> >queue.append(node.left)> >if> node.right:> >parentMap[node.right]>=> node> >queue.append(node.right)> >return> parentMap> # Function to find the lowest common ancestor of two nodes> # using an auxiliary data structure> def> findLCA(root, n1, n2):> ># Build a hash table or a map of parent pointers for> ># each node in the tree> >parentMap>=> buildParentMap(root)> ># Find the nodes with values n1 and n2> >p, q>=> None>,>None> >queue>=> deque([root])> >while> queue:> >node>=> queue.popleft()> >if> node.data>=>=> n1:> >p>=> node> >if> node.data>=>=> n2:> >q>=> node> >if> node.left:> >queue.append(node.left)> >if> node.right:> >queue.append(node.right)> ># Add all the ancestors of the first node to a set or a> ># list> >ancestors>=> set>()> >while> p:> >ancestors.add(p)> >p>=> parentMap[p]> ># Traverse up from the second node and check if each> ># ancestor is already in the set or the list> >while> q:> >if> q>in> ancestors:> >return> q.data> >q>=> parentMap[q]> >return> ->1> # No common ancestor found> # Driver code> if> __name__>=>=> '__main__'>:> >root>=> Node(>1>)> >root.left>=> Node(>2>)> >root.right>=> Node(>3>)> >root.left.left>=> Node(>4>)> >root.left.right>=> Node(>5>)> >root.right.left>=> Node(>6>)> >root.right.right>=> Node(>7>)> >print>(>'LCA(4, 5) = '>, findLCA(root,>4>,>5>))> >print>(>'LCA(4, 6) = '>, findLCA(root,>4>,>6>))> >print>(>'LCA(3, 4) = '>, findLCA(root,>3>,>4>))> >print>(>'LCA(2, 4) = '>, findLCA(root,>2>,>4>))>

C#

using> System;> using> System.Collections.Generic;> // Definition of a binary tree node> class> Node> {> >public> int> data;> >public> Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> class> MainClass> {> >// Function to build a hash table or a map of parent> >// pointers for each node in the tree> >static> Dictionary BuildParentMap(Node root)> >{> >Dictionary parentMap =>new> Dictionary();> >parentMap.Add(root,>null>);> >Queue queue =>new> Queue();> >queue.Enqueue(root);> >while> (queue.Count != 0)> >{> >Node node = queue.Dequeue();> >if> (node.left !=>null>)> >{> >parentMap.Add(node.left, node);> >queue.Enqueue(node.left);> >}> >if> (node.right !=>null>)> >{> >parentMap.Add(node.right, node);> >queue.Enqueue(node.right);> >}> >}> >return> parentMap;> >}> >// Function to find the lowest common ancestor of two> >// nodes using an auxiliary data structure> >static> int> FindLCA(Node root,>int> n1,>int> n2)> >{> >// Build a hash table or a map of parent pointers> >// for each node in the tree> >Dictionary parentMap = BuildParentMap(root);> >// Find the nodes with values n1 and n2> >Node p =>null>, q =>null>;> >Queue queue =>new> Queue();> >queue.Enqueue(root);> >while> (queue.Count != 0)> >{> >Node node = queue.Dequeue();> >if> (node.data == n1)> >{> >p = node;> >}> >if> (node.data == n2)> >{> >q = node;> >}> >if> (node.left !=>null>)> >{> >queue.Enqueue(node.left);> >}> >if> (node.right !=>null>)> >{> >queue.Enqueue(node.right);> >}> >}> >// Add all the ancestors of the first node to a set> >// or a list> >HashSet ancestors =>new> HashSet();> >while> (p !=>null>)> >{> >ancestors.Add(p);> >p = parentMap[p];> >}> >// Traverse up from the second node and check if> >// each ancestor is already in the set or the list> >while> (q !=>null>)> >{> >if> (ancestors.Contains(q))> >{> >return> q.data;> >}> >q = parentMap[q];> >}> >return> -1;>// No common ancestor found> >}> >public> static> void> Main()> >{> >Node root =>new> Node(1);> >root.left =>new> Node(2);> >root.right =>new> Node(3);> >root.left.left =>new> Node(4);> >root.left.right =>new> Node(5);> >root.right.left =>new> Node(6);> >root.right.right =>new> Node(7);> >Console.WriteLine(>'LCA(4, 5) = '> + FindLCA(root, 4, 5));> >Console.WriteLine(>'LCA(4, 6) = '> + FindLCA(root, 4, 6));> >Console.WriteLine(>'LCA(3, 4) = '> + FindLCA(root, 3, 4));> >Console.WriteLine(>'LCA(2, 4) = '> + FindLCA(root, 2, 4));> >}> }> // This code is contributed by akashish__>

Javascript

// javascript code addition> // Definition of a binary tree node> class Node {> >constructor(item) {> >this>.data = item;> >this>.left =>null>;> >this>.right =>null>;> >}> }> // Function to build a hash table or a map of parent> // pointers for each node in the tree> function> buildParentMap(root) {> >const parentMap =>new> Map();> >parentMap.set(root,>null>);> >const queue = [];> >queue.push(root);> >while> (queue.length>0) {> >const node = queue.shift();> >if> (node.left !=>null>) {> >parentMap.set(node.left, node);> >queue.push(node.left);> >}> >if> (node.right !=>null>) {> >parentMap.set(node.right, node);> >queue.push(node.right);> >}> >}> >return> parentMap;> }> // Function to find the lowest common ancestor of two> // nodes using an auxiliary data structure> function> findLCA(root, n1, n2) {> >// Build a hash table or a map of parent pointers> >// for each node in the tree> >const parentMap = buildParentMap(root);> >// Find the nodes with values n1 and n2> >let p =>null>, q =>null>;> >const queue = [];> >queue.push(root);> >while> (queue.length>0) {> >const node = queue.shift();> >if> (node.data === n1) {> >p = node;> >}> >if> (node.data === n2) {> >q = node;> >}> >if> (node.left !=>null>) {> >queue.push(node.left);> >}> >if> (node.right !=>null>) {> >queue.push(node.right);> >}> >}> >// Add all the ancestors of the first node to a set> >// or a list> >const ancestors =>new> Set();> >while> (p !=>null>) {> >ancestors.add(p);> >p = parentMap.get(p);> >}> >// Traverse up from the second node and check if> >// each ancestor is already in the set or the list> >while> (q !=>null>) {> >if> (ancestors.has(q)) {> >return> q.data;> >}> >q = parentMap.get(q);> >}> >return> -1;>// No common ancestor found> }> // Test the function> const root =>new> Node(1);> root.left =>new> Node(2);> root.right =>new> Node(3);> root.left.left =>new> Node(4);> root.left.right =>new> Node(5);> root.right.left =>new> Node(6);> root.right.right =>new> Node(7);> console.log(>'LCA(4, 5) = '> + findLCA(root, 4, 5));> console.log(>'LCA(4, 6) = '> + findLCA(root, 4, 6));> console.log(>'LCA(3, 4) = '> + findLCA(root, 3, 4));> console.log(>'LCA(2, 4) = '> + findLCA(root, 2, 4));> // The code is contributed by Nidhi goel.>

Sortir

LCA(4, 5) = 2 LCA(4, 6) = 1 LCA(3,4) = 1 LCA(2, 4) = 2>

Complexité temporelle : O(n),

langage informatique génial

La complexité temporelle du code donné est O(n), où n est le nombre de nœuds dans l'arbre binaire.

Construire la carte parent pour chaque nœud de l'arborescence nécessite de visiter chaque nœud une fois, ce qui prend un temps O(n). Trouver les nœuds avec les valeurs n1 et n2 nécessite de visiter chaque nœud une fois, ce qui prend également un temps O(n). Traverser à partir du deuxième nœud et vérifier si chaque ancêtre est déjà dans l'ensemble ou si la liste prend un temps O(h), où h est la hauteur de l'arbre binaire.

Dans le pire des cas, la hauteur de l'arbre binaire est O(n), si l'arbre binaire est asymétrique. Par conséquent, la complexité temporelle globale du code donné est O(n) + O(n) + O(n) = O(n).

Complexité spatiale : O(n),

La complexité spatiale du code donné est O(n) dans le pire des cas. En effet, la taille de la carte parent construite pour chaque nœud de l'arborescence est O(n). De plus, l'ensemble des ancêtres peut également contenir tous les nœuds de l'arbre binaire dans le pire des cas, ce qui prend également de l'espace O(n). Enfin, la file d'attente utilisée pour parcourir l'arbre binaire prend de l'espace O(n). Par conséquent, la complexité spatiale globale du code donné est O(n) + O(n) + O(n) = O(n).

Nous avons discuté d'une solution efficace pour trouver LCA dans l'arbre de recherche binaire. Dans l'arbre de recherche binaire, en utilisant les propriétés BST, nous pouvons trouver LCA en un temps O(h) où h est la hauteur de l'arbre. Une telle implémentation n'est pas possible dans Binary Tree car les clés des nœuds de l'arbre binaire ne suivent aucun ordre.

Vous aimerez peut-être également consulter les articles ci-dessous :
ACV utilisant le pointeur parent
Ancêtre commun le plus bas dans un arbre de recherche binaire.
Rechercher LCA dans l'arbre binaire à l'aide de RMQ