SOUS-SÉQUENCE COMMUNE LA PLUS LONGUE (LCS) - TECHCODEVIEW.COM

Étant donné deux chaînes, S1 et S2 , la tâche consiste à trouver la longueur de la sous-séquence commune la plus longue, c'est-à-dire la sous-séquence la plus longue présente dans les deux chaînes.

UN sous-séquence commune la plus longue (LCS) est défini comme la sous-séquence la plus longue commune à toutes les séquences d’entrée données.

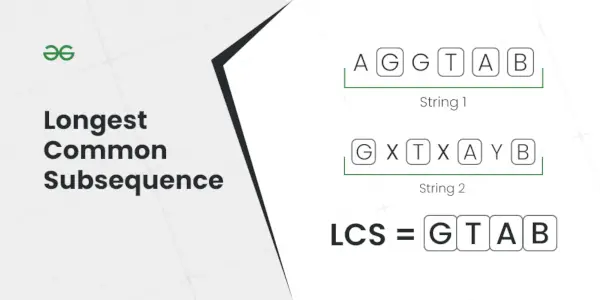
Sous-séquence commune la plus longue

Exemples:

Saisir: S1 = ABC, S2 = ACD
Sortir: 2
Explication: La sous-séquence la plus longue présente dans les deux chaînes est AC.

Saisir: S1 = AGGTAB, S2 = GXTXAYB
Sortir: 4
Explication: La sous-séquence commune la plus longue est GTAB.

Saisir: S1 = ABC, S2 = ABC
Sortir: 1
Explication: Il existe trois sous-séquences communes de longueur 1, A, B et C et aucune sous-séquence commune de longueur supérieure à 1.

Saisir: S1 = XYZW, S2 = XYWZ
Sortir: 3
Explication: Il existe deux sous-séquences communes de longueur 3 XYZ et XYW, et aucune sous-séquence commune. de longueur supérieure à 3.
java mathématiques

Pratique recommandée Sous-séquence commune la plus longue Essayez-le !

Sous-séquence commune la plus longue (LCS) utilisant la récursion :

Générez toutes les sous-séquences possibles et trouvez la plus longue d'entre elles présente dans les deux chaînes en utilisant Suivez les étapes ci-dessous pour mettre en œuvre l'idée :

Créez une fonction récursive [disons lcs() ].
Vérifiez la relation entre les premiers caractères des chaînes qui ne sont pas encore traitées.
- En fonction de la relation, appelez la fonction récursive suivante comme mentionné ci-dessus.
Renvoie la longueur du LCS reçu comme réponse.

Ci-dessous la mise en œuvre de l'approche récursive :

C++

 // A Naive recursive implementation of LCS problem #include  using namespace std; // Returns length of LCS for X[0..m-1], Y[0..n-1] int lcs(string X, string Y, int m, int n)  // Driver code int main() {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  int m = S1.size();  int n = S2.size();  cout << 'Length of LCS is ' << lcs(S1, S2, m, n);  return 0; } // This code is contributed by rathbhupendra>

 // A Naive recursive implementation // of LCS problem #include  int max(int a, int b); // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(char* X, char* Y, int i, int j)  // Utility function to get max of // 2 integers int max(int a, int b) { return (a>b) ? un B; } // Code du pilote int main() { char S1[] = 'BD';  char S2[] = 'ABCD';  int m = strlen(S1);  int n = strlen(S2);  int je = 0, j = 0;  // Appel de fonction printf('La longueur du LCS est %d', lcs(S1, S2, i, j));  renvoie 0 ; }>

Java

 // A Naive recursive implementation of LCS problem in java import java.io.*; import java.util.*; public class LongestCommonSubsequence {  // Returns length of LCS for X[0..m-1], Y[0..n-1]  int lcs(String X, String Y, int m, int n)   n == 0)  return 0;  if (X.charAt(m - 1) == Y.charAt(n - 1))  return 1 + lcs(X, Y, m - 1, n - 1);  else  return max(lcs(X, Y, m, n - 1),  lcs(X, Y, m - 1, n));    // Utility function to get max of 2 integers  int max(int a, int b) { return (a>b) ? un B; } // Code du pilote public static void main(String[] args) { LongestCommonSubsequence lcs = new LongestCommonSubsequence();  Chaîne S1 = 'AGGTAB';  Chaîne S2 = 'GXTXAYB';  int m = S1.longueur();  int n = S2.longueur();  System.out.println('La longueur du LCS est' + ' ' + lcs.lcs(S1, S2, m, n));  } } // Ce code provient de Saket Kumar>

Python

 # A Naive recursive Python implementation of LCS problem def lcs(X, Y, m, n): if m == 0 or n == 0: return 0 elif X[m-1] == Y[n-1]: return 1 + lcs(X, Y, m-1, n-1) else: return max(lcs(X, Y, m, n-1), lcs(X, Y, m-1, n)) # Driver code if __name__ == '__main__': S1 = 'AGGTAB' S2 = 'GXTXAYB' print('Length of LCS is', lcs(S1, S2, len(S1), len(S2)))>

 // C# Naive recursive implementation of LCS problem using System; class GFG {  // Returns length of LCS for X[0..m-1], Y[0..n-1]  static int lcs(String X, String Y, int m, int n)    if (m == 0   // Utility function to get max of 2 integers  static int max(int a, int b) { return (a>b) ? un B; } // Code du pilote public static void Main() { String S1 = 'AGGTAB';  Chaîne S2 = 'GXTXAYB';  int m = S1.Longueur ;  int n = S2.Longueur ;  Console.Write('La longueur du LCS est' + ' ' + lcs(S1, S2, m, n));  } } // Ce code est contribué par Sam007>

Javascript

PHP

  // A Naive recursive PHP  // implementation of LCS problem  function lcs($X, $Y, $m, $n)  $n == 0) return 0; else if ($X[$m - 1] == $Y[$n - 1]) return 1 + lcs($X, $Y, $m - 1, $n - 1); else return max(lcs($X, $Y, $m, $n - 1), lcs($X, $Y, $m - 1, $n));  // Driver Code  $S1 = 'AGGTAB'; $S2 = 'GXTXAYB'; echo 'Length of LCS is '; echo lcs($S1 , $S2, strlen($S1), strlen($S2)); // This code is contributed  // by Shivi_Aggarwal  ?>>

Sortir

Length of LCS is 4>

Complexité temporelle : O(2^m+n)
Espace auxiliaire : O(1)

Sous-séquence commune la plus longue (LCS) utilisant Mémorisation :

Si nous y prêtons attention, nous pouvons observer que la solution récursive ci-dessus possède les deux propriétés suivantes :

1. Sous-structure optimale :

Voir pour résoudre la structure de L(X[0, 1, . . ., m-1], Y[0, 1, . . . , n-1]), nous prenons l'aide des sous-structures de X[0 , 1, …, m-2], Y[0, 1,…, n-2], selon la situation (c'est-à-dire les utiliser de manière optimale) pour trouver la solution de l'ensemble.

topologies

2. Sous-problèmes qui se chevauchent :

Si nous utilisons l'approche récursive ci-dessus pour les chaînes BD et A B C D , nous obtiendrons un arbre de récursivité partiel comme indiqué ci-dessous. Ici, nous pouvons voir que le sous-problème L(BD, ABCD) est calculé plus d’une fois. Si l’on considère l’arbre total, il y aura plusieurs sous-problèmes qui se chevauchent.

L(AXYT, AYZX)
/
L(AXY, AYZX) L(AXYT, AYZ)
//
L(AX, AYZX) L(AXY, AYZ) L(AXY, AYZ) L(AXYT, AY)

Approche: En raison de la présence de ces deux propriétés, nous pouvons utiliser la programmation dynamique ou la mémorisation pour résoudre le problème. Vous trouverez ci-dessous l'approche de la solution utilisant la récursivité.

Créez une fonction récursive. Créez également un tableau 2D pour stocker le résultat d'un état unique.
Lors de l'appel récursif, si le même état est appelé plus d'une fois, nous pouvons alors renvoyer directement la réponse stockée pour cet état au lieu de recalculer.

Vous trouverez ci-dessous la mise en œuvre de l’approche ci-dessus :

C++

 // A Top-Down DP implementation // of LCS problem #include  using namespace std; // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(char* X, char* Y, int m, int n,  vector>& dp) { if (m == 0 || n == 0) renvoie 0;  if (X[m - 1] == Y[n - 1]) return dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp);  if (dp[m][n] != -1) { return dp[m][n];  } return dp[m][n] = max(lcs(X, Y, m, n - 1, dp), lcs(X, Y, m - 1, n, dp)); } // Code du pilote int main() { char X[] = 'AGGTAB';  char Y[] = 'GXTXAYB';  int m = strlen(X);  int n = strlen(Y);  vecteur> dp(m + 1, vecteur (n + 1, -1));  cout<< 'Length of LCS is ' << lcs(X, Y, m, n, dp);  return 0; }>

Java

 /*package whatever //do not write package name here */ import java.io.*; class GFG {  // A Top-Down DP implementation of LCS problem  // Returns length of LCS for X[0..m-1], Y[0..n-1]  static int lcs(String X, String Y, int m, int n,  int[][] dp)  {  if (m == 0 || n == 0)  return 0;  if (dp[m][n] != -1)  return dp[m][n];  if (X.charAt(m - 1) == Y.charAt(n - 1)) {  dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp);  return dp[m][n];  }  dp[m][n] = Math.max(lcs(X, Y, m, n - 1, dp),  lcs(X, Y, m - 1, n, dp));  return dp[m][n];  }  // Drivers code  public static void main(String args[])  {  String X = 'AGGTAB';  String Y = 'GXTXAYB';  int m = X.length();  int n = Y.length();  int[][] dp = new int[m + 1][n + 1];  for (int i = 0; i < m + 1; i++) {  for (int j = 0; j < n + 1; j++) {  dp[i][j] = -1;  }  }  System.out.println('Length of LCS is '  + lcs(X, Y, m, n, dp));  } } // This code is contributed by shinjanpatra>

Python

 # A Top-Down DP implementation of LCS problem # Returns length of LCS for X[0..m-1], Y[0..n-1] def lcs(X, Y, m, n, dp): if (m == 0 or n == 0): return 0 if (dp[m][n] != -1): return dp[m][n] if X[m - 1] == Y[n - 1]: dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp) return dp[m][n] dp[m][n] = max(lcs(X, Y, m, n - 1, dp), lcs(X, Y, m - 1, n, dp)) return dp[m][n] # Driver code X = 'AGGTAB' Y = 'GXTXAYB' m = len(X) n = len(Y) dp = [[-1 for i in range(n + 1)]for j in range(m + 1)] print(f'Length of LCS is {lcs(X, Y, m, n, dp)}') # This code is contributed by shinjanpatra>

 /* C# Naive recursive implementation of LCS problem */ using System; class GFG {  /* Returns length of LCS for X[0..m-1], Y[0..n-1] */  static int lcs(char[] X, char[] Y, int m, int n,  int[, ] L)  {  if (m == 0 || n == 0)  return 0;  if (L[m, n] != -1)  return L[m, n];  if (X[m - 1] == Y[n - 1]) {  L[m, n] = 1 + lcs(X, Y, m - 1, n - 1, L);  return L[m, n];  }  L[m, n] = max(lcs(X, Y, m, n - 1, L),  lcs(X, Y, m - 1, n, L));  return L[m, n];  }  /* Utility function to get max of 2 integers */  static int max(int a, int b) { return (a>b) ? un B; } public static void Main() { Chaîne s1 = 'AGGTAB';  Chaîne s2 = 'GXTXAYB';  char[] X = s1.ToCharArray();  char[] Y = s2.ToCharArray();  int m = X.Longueur ;  int n = Y.Longueur ;  int[, ] L = nouveau int[m + 1, n + 1];  pour (int je = 0; je<= m; i++) {  for (int j = 0; j <= n; j++) {  L[i, j] = -1;  }  }  Console.Write('Length of LCS is'  + ' ' + lcs(X, Y, m, n, L));  } } // This code is contributed by akshitsaxenaa09>

Javascript

 /* A Top-Down DP implementation of LCS problem */ /* Returns length of LCS for X[0..m-1], Y[0..n-1] */ function lcs(X, Y, m, n, dp) {  if (m == 0 || n == 0)  return 0;  if (X[m - 1] == Y[n - 1])  return dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp);  if (dp[m][n] != -1) {  return dp[m][n];  }  return dp[m][n] = Math.max(lcs(X, Y, m, n - 1, dp),  lcs(X, Y, m - 1, n, dp)); } /* Driver code */ let X = 'AGGTAB'; let Y = 'GXTXAYB'; let m = X.length; let n = Y.length; let dp = new Array(m + 1); for(let i = 0; i < m + 1; i++) {  dp[i] = new Array(n + 1).fill(-1); }  console.log('Length of LCS is ' + lcs(X, Y, m, n, dp)); // This code is contributed by shinjanpatra>

Sortir

Length of LCS is 4>

Complexité temporelle : O(m * n) où m et n sont les longueurs de chaîne.
Espace auxiliaire : O(m * n) Ici, l'espace de pile récursive est ignoré.

Sous-séquence commune la plus longue (LCS) utilisant la méthode ascendante (tabulation) :

Nous pouvons utiliser les étapes suivantes pour implémenter l'approche de programmation dynamique pour LCS.

Créer un tableau 2D dp[][] avec des lignes et des colonnes égales à la longueur de chaque chaîne d'entrée plus 1 [le nombre de lignes indique les indices de S1 et les colonnes indiquent les indices de S2 ].
Initialisez la première ligne et la première colonne du tableau dp à 0.
Parcourez les lignes du tableau dp, en commençant par 1 (par exemple en utilisant l'itérateur je ).
- Pour chaque je , parcourez toutes les colonnes de j = 1 à n :
  - Si S1[je-1] est égal à S2[j-1] , définissez l'élément actuel du tableau dp sur la valeur de l'élément à ( dp[i-1][j-1] + 1 ).
  - Sinon, définissez l'élément actuel du tableau dp sur la valeur maximale de dp[je-1][j] et dp[i][j-1] .
Après les boucles imbriquées, le dernier élément du tableau dp contiendra la longueur du LCS.

Voir l'illustration ci-dessous pour une meilleure compréhension :

Illustration:

Disons que les chaînes sont S1 = AGGTAB et S2 = GXTXAYB .

Premier pas: Créez initialement une matrice 2D (disons dp[][]) de taille 8 x 7 dont la première ligne et la première colonne sont remplies de 0.

Création de la table dp
Deuxième étape: Traversée pour i = 1. Lorsque j devient 5, S1[0] et S2[4] sont égaux. Le dp[][] est donc mis à jour. Pour les autres éléments prendre le maximum de dp[i-1][j] et dp[i][j-1]. (Dans ce cas, si les deux valeurs sont égales, nous avons utilisé des flèches vers les lignes précédentes).

Remplir la ligne n°1
Troisième étape: Bien que parcourus pour i = 2, S1[1] et S2[0] sont identiques (les deux sont « G »). La valeur dp dans cette cellule est donc mise à jour. Le reste des éléments est mis à jour selon les conditions.
le pivot du panda

Remplir la ligne no. 2
Quatrième étape : Pour i = 3, S1[2] et S2[0] sont à nouveau identiques. Les mises à jour sont les suivantes.

Remplissage de la ligne no. 3
Cinquième étape : Pour i = 4, nous pouvons voir que S1[3] et S2[2] sont identiques. Donc dp[4][3] mis à jour comme dp[3][2] + 1 = 2.

Remplissage de la ligne 4
Sixième étape : Ici, nous pouvons voir que pour i = 5 et j = 5, les valeurs de S1[4] et S2[4] sont les mêmes (c'est-à-dire que les deux sont « A »). Donc dp[5][5] est mis à jour en conséquence et devient 3.

Remplissage de la ligne 5
Dernière étape: Pour i = 6, voyez que les derniers caractères des deux chaînes sont identiques (ce sont « B »). La valeur de dp[6][7] devient donc 4.

Remplir la dernière ligne
java booléen
Nous obtenons donc la longueur maximale de la sous-séquence commune comme 4 .

Voici une implémentation tabulée du problème LCS.

C++

 // Dynamic Programming C++ implementation // of LCS problem #include  using namespace std; // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(string X, string Y, int m, int n) {  // Initializing a matrix of size  // (m+1)*(n+1)  int L[m + 1][n + 1];  // Following steps build L[m+1][n+1]  // in bottom up fashion. Note that  // L[i][j] contains length of LCS of  // X[0..i-1] and Y[0..j-1]  for (int i = 0; i <= m; i++) {  for (int j = 0; j <= n; j++)   if (i == 0   }  // L[m][n] contains length of LCS  // for X[0..n-1] and Y[0..m-1]  return L[m][n]; } // Driver code int main() {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  int m = S1.size();  int n = S2.size();  // Function call  cout << 'Length of LCS is ' << lcs(S1, S2, m, n);  return 0; }>

Java

 // Dynamic Programming Java implementation of LCS problem import java.util.*; public class LongestCommonSubsequence {  // Returns length of LCS for X[0..m-1], Y[0..n-1]  int lcs(String X, String Y, int m, int n)  {  int L[][] = new int[m + 1][n + 1];  // Following steps build L[m+1][n+1] in bottom up  // fashion. Note that L[i][j] contains length of LCS  // of X[0..i-1] and Y[0..j-1]  for (int i = 0; i <= m; i++) {  for (int j = 0; j <= n; j++)  j == 0)  L[i][j] = 0;  else if (X.charAt(i - 1) == Y.charAt(j - 1))  L[i][j] = L[i - 1][j - 1] + 1;  else  L[i][j] = max(L[i - 1][j], L[i][j - 1]);    }  return L[m][n];  }  // Utility function to get max of 2 integers  int max(int a, int b) { return (a>b) ? un B; } public static void main(String[] args) { LongestCommonSubsequence lcs = new LongestCommonSubsequence();  Chaîne S1 = 'AGGTAB';  Chaîne S2 = 'GXTXAYB';  int m = S1.longueur();  int n = S2.longueur();  System.out.println('La longueur du LCS est' + ' ' + lcs.lcs(S1, S2, m, n));  } } // Ce code provient de Saket Kumar>

Python

 # Dynamic Programming implementation of LCS problem def lcs(X, Y, m, n): # Declaring the array for storing the dp values L = [[None]*(n+1) for i in range(m+1)] # Following steps build L[m+1][n+1] in bottom up fashion # Note: L[i][j] contains length of LCS of X[0..i-1] # and Y[0..j-1] for i in range(m+1): for j in range(n+1): if i == 0 or j == 0: L[i][j] = 0 elif X[i-1] == Y[j-1]: L[i][j] = L[i-1][j-1]+1 else: L[i][j] = max(L[i-1][j], L[i][j-1]) # L[m][n] contains the length of LCS of X[0..n-1] & Y[0..m-1] return L[m][n] # Driver code if __name__ == '__main__': S1 = 'AGGTAB' S2 = 'GXTXAYB' m = len(S1) n = len(S2) print('Length of LCS is', lcs(S1, S2, m, n)) # This code is contributed by Nikhil Kumar Singh(nickzuck_007)>

 // Dynamic Programming implementation of LCS problem using System; class GFG {  // Returns length of LCS for X[0..m-1], Y[0..n-1]  static int lcs(String X, String Y, int m, int n)  {  int[, ] L = new int[m + 1, n + 1];  // Following steps build L[m+1][n+1]  // in bottom up fashion.  // Note that L[i][j] contains length of  // LCS of X[0..i-1] and Y[0..j-1]  for (int i = 0; i <= m; i++) {  for (int j = 0; j <= n; j++)  j == 0)  L[i, j] = 0;  else if (X[i - 1] == Y[j - 1])  L[i, j] = L[i - 1, j - 1] + 1;  else  L[i, j] = max(L[i - 1, j], L[i, j - 1]);    }  return L[m, n];  }  // Utility function to get max of 2 integers  static int max(int a, int b) { return (a>b) ? un B; } // Code du pilote public static void Main() { String S1 = 'AGGTAB';  Chaîne S2 = 'GXTXAYB';  int m = S1.Longueur ;  int n = S2.Longueur ;  Console.Write('La longueur du LCS est' + ' ' + lcs(S1, S2, m, n));  } } // Ce code provient de Sam007>

Javascript

 // Dynamic Programming Java implementation of LCS problem // Utility function to get max of 2 integers  function max(a, b) {  if (a>b) renvoyer a ;  sinon, retourne b; } // Renvoie la longueur du LCS pour X[0..m-1], Y[0..n-1] function lcs(X, Y, m, n) { var L = new Array(m + 1);  pour(var je = 0; je< L.length; i++)   {  L[i] = new Array(n + 1);  }  var i, j;    /* Following steps build L[m+1][n+1] in  bottom up fashion. Note that L[i][j]  contains length of LCS of X[0..i-1]  and Y[0..j-1] */  for(i = 0; i <= m; i++)  {  for(j = 0; j <= n; j++)   j == 0)  L[i][j] = 0;  else if (X[i - 1] == Y[j - 1])  L[i][j] = L[i - 1][j - 1] + 1;  else  L[i][j] = max(L[i - 1][j], L[i][j - 1]);    }    /* L[m][n] contains length of LCS  for X[0..n-1] and Y[0..m-1] */  return L[m][n]; } // Driver code var S1 = 'AGGTAB'; var S2 = 'GXTXAYB'; var m = S1.length; var n = S2.length; console.log('Length of LCS is ' + lcs(S1, S2, m, n)); // This code is contributed by akshitsaxenaa09>

PHP

  // Dynamic Programming C#  // implementation of LCS problem  function lcs($X , $Y, $m, $n) { // Following steps build L[m+1][n+1]  // in bottom up fashion .  // Note: L[i][j] contains length of  // LCS of X[0..i-1] and Y[0..j-1] for ($i = 0; $i <= $m; $i++) { for ($j = 0; $j <= $n; $j++)  if ($i == 0  } // L[m][n] contains the length of  // LCS of X[0..n-1] & Y[0..m-1]  return $L[$m][$n]; } // Driver Code  $S1 = 'AGGTAB'; $S2 = 'GXTXAYB'; $m = strlen($S1); $n = strlen($S2) ; echo 'Length of LCS is '; echo lcs($S1, $S2, $m, $n); // This code is contributed  // by Shivi_Aggarwal  ?>>

Sortir

Length of LCS is 4>

Complexité temporelle : O(m * n), ce qui est bien meilleur que la complexité temporelle dans le pire des cas de l'implémentation Naive Recursive.
Espace auxiliaire : O(m * n) car l'algorithme utilise un tableau de taille (m+1)*(n+1) pour stocker la longueur des sous-chaînes communes.

Sous-séquence commune la plus longue (LCS) utilisant la méthode ascendante (optimisation de l'espace) :

Dans l'approche de tabulation ci-dessus, nous utilisons L[i-1][j] et L[i][j] etc., ici le L[i-1] fera référence à la ligne précédente de la matrice L et L[i] fera référence à la ligne actuelle.
Nous pouvons optimiser l'espace en utilisant deux vecteurs, l'un est précédent et l'autre est actuel.
Lorsque la boucle for interne se termine, nous initialisons le précédent égal au courant.

Ci-dessous la mise en œuvre :

C++

 // Dynamic Programming C++ implementation // of LCS problem #include  using namespace std; int longestCommonSubsequence(string& text1, string& text2) {  int n = text1.size();  int m = text2.size();  // initializing 2 vectors of size m  vector précédent(m + 1, 0), cur(m + 1, 0);  pour (int idx2 = 0; idx2< m + 1; idx2++)  cur[idx2] = 0;  for (int idx1 = 1; idx1 < n + 1; idx1++) {  for (int idx2 = 1; idx2 < m + 1; idx2++) {  // if matching  if (text1[idx1 - 1] == text2[idx2 - 1])  cur[idx2] = 1 + prev[idx2 - 1];  // not matching  else  cur[idx2]  = 0 + max(cur[idx2 - 1], prev[idx2]);  }  prev = cur;  }  return cur[m]; } int main() {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  // Function call  cout << 'Length of LCS is '  << longestCommonSubsequence(S1, S2);  return 0; }>

Java

 // Dynamic Programming Java implementation of LCS problem import java.util.Arrays; public class GFG {  public static int longestCommonSubsequence(String text1, String text2) {  int n = text1.length();  int m = text2.length();  // Initializing 2 arrays of size m  int[] prev = new int[m + 1];  int[] cur = new int[m + 1];  for (int idx1 = 1; idx1 < n + 1; idx1++) {  for (int idx2 = 1; idx2 < m + 1; idx2++) {  // If matching  if (text1.charAt(idx1 - 1) == text2.charAt(idx2 - 1))  cur[idx2] = 1 + prev[idx2 - 1];  // Not matching  else  cur[idx2] = Math.max(cur[idx2 - 1], prev[idx2]);  }  prev = Arrays.copyOf(cur, m + 1);  }  return cur[m];  }  public static void main(String[] args) {  String S1 = 'AGGTAB';  String S2 = 'GXTXAYB';  // Function call  System.out.println('Length of LCS is ' + longestCommonSubsequence(S1, S2));  } }>

Python

 def longestCommonSubsequence(text1, text2): n = len(text1) m = len(text2) # Initializing two lists of size m prev = [0] * (m + 1) cur = [0] * (m + 1) for idx1 in range(1, n + 1): for idx2 in range(1, m + 1): # If characters are matching if text1[idx1 - 1] == text2[idx2 - 1]: cur[idx2] = 1 + prev[idx2 - 1] else: # If characters are not matching cur[idx2] = max(cur[idx2 - 1], prev[idx2]) prev = cur.copy() return cur[m] if __name__ == '__main__': S1 = 'AGGTAB' S2 = 'GXTXAYB' # Function call print('Length of LCS is', longestCommonSubsequence(S1, S2)) # This code is contributed by Rishabh Mathur>

 using System; class Program {  static int LongestCommonSubsequence(string text1, string text2)  {  int n = text1.Length;  int m = text2.Length;  // initializing 2 arrays of size m  int[] prev = new int[m + 1];  int[] cur = new int[m + 1];  for (int idx2 = 0; idx2 < m + 1; idx2++)  cur[idx2] = 0;  for (int idx1 = 1; idx1 < n + 1; idx1++)  {  for (int idx2 = 1; idx2 < m + 1; idx2++)  {  // if matching  if (text1[idx1 - 1] == text2[idx2 - 1])  cur[idx2] = 1 + prev[idx2 - 1];  // not matching  else  cur[idx2] = 0 + Math.Max(cur[idx2 - 1], prev[idx2]);  }  prev = cur;  }  return cur[m];  }  static void Main()  {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  // Function call  Console.WriteLine('Length of LCS is ' + LongestCommonSubsequence(S1, S2));  } }>

Javascript

 function longestCommonSubsequence(text1, text2) {  const n = text1.length;  const m = text2.length;  // Initializing two arrays of size m  let prev = new Array(m + 1).fill(0);  let cur = new Array(m + 1).fill(0);  for (let idx2 = 0; idx2 < m + 1; idx2++) {  cur[idx2] = 0;  }  for (let idx1 = 1; idx1 < n + 1; idx1++) {  for (let idx2 = 1; idx2 < m + 1; idx2++) {  // If characters match  if (text1[idx1 - 1] === text2[idx2 - 1]) {  cur[idx2] = 1 + prev[idx2 - 1];  }  // If characters don't match  else {  cur[idx2] = Math.max(cur[idx2 - 1], prev[idx2]);  }  }  // Update the 'prev' array  prev = [...cur];  }  return cur[m]; } // Main function function main() {  const S1 = 'AGGTAB';  const S2 = 'GXTXAYB';  // Function call  console.log('Length of LCS is ' + longestCommonSubsequence(S1, S2)); } // Call the main function main();>

Sortir

Length of LCS is 4>

Complexité temporelle : O(m * n), qui reste le même.
Espace auxiliaire : O(m) car l'algorithme utilise deux tableaux de taille m.