Le terme Mémorisation vient du mot latin mémorandum ( se souvenir ), qui est communément abrégé en mémo en anglais américain, et qui signifie transformer les résultats d'une fonction en quelque chose à retenir.
En informatique, la mémorisation est utilisée pour accélérer les programmes informatiques en éliminant le calcul répétitif des résultats et en évitant les appels répétés aux fonctions qui traitent la même entrée.

Qu'est-ce que la mémorisation
Table des matières
- Qu’est-ce que la mémorisation ?
- Pourquoi la mémisation est-elle utilisée >
- Où utiliser la mémorisation ?
- Types de mémorisation
- Comment la technique de mémorisation est-elle utilisée en programmation dynamique ?
- En quoi la mémorisation est-elle différente de la tabulation ?
- Problèmes de pratique de codage pour la mémorisation
- FAQ
- 1) La mémorisation est-elle meilleure que DP ?
- 2) La mémorisation est-elle la même chose que la mise en cache ?
- 3) Pourquoi la mémorisation est descendante ?
- 4) La mémorisation utilise-t-elle la récursion ?
- 5) Dois-je utiliser la tabulation ou la mémorisation ?
- 6) Où la mémorisation est-elle utilisée ?
- 7) Pourquoi cela s’appelle-t-on mémorisation ?
- 8) Comment la mémorisation réduit-elle la complexité temporelle ?
- 9) Quelle est la différence entre la mémorisation et la mise en cache ?
- 10) Pourquoi la tabulation est plus rapide que la mémorisation ?
- Conclusion
Pourquoi la mémorisation est-elle utilisée ?
La mémorisation est une forme spécifique de mise en cache qui est utilisé dans programmation dynamique . Le but de la mise en cache est d'améliorer les performances de nos programmes et de garder les données accessibles qui pourront être utilisées ultérieurement. Il stocke essentiellement le résultat précédemment calculé du sous-problème et utilise le résultat stocké pour le même sous-problème. Cela supprime l'effort supplémentaire nécessaire pour calculer encore et encore pour le même problème. Et nous savons déjà que si le même problème se reproduit encore et encore, alors ce problème est de nature récursive.
Où utiliser la mémorisation ?
Nous pouvons utiliser la technique de mémorisation où le utilisation des résultats calculés précédemment entre en scène. Ce type de problème est surtout utilisé dans le contexte de récursivité , en particulier avec les problèmes qui impliquent sous-problèmes qui se chevauchent .
Prenons un exemple où le même sous-problème se répète encore et encore.
Exemple pour montrer où utiliser la mémorisation :
Let us try to find the factorial of a number .>
Ci-dessous se trouve un méthode récursive pour trouver la factorielle d'un nombre :
int factoriel (entier non signé n)
{
si (n == 0)
renvoyer 1 ;
retourner n * factoriel(n – 1);
}
Que se passe-t-il si nous utilisons cette méthode récursive ?
Si vous écrivez le code complet de l'extrait ci-dessus, vous remarquerez qu'il y aura 2 méthodes dans le code :
1. factorial(n) 2. main()>
Maintenant, si nous avons plusieurs requêtes pour trouver la factorielle, comme trouver une factorielle de 2, 3, 9 et 5, nous devrons alors appeler la méthode factorial() 4 fois :
factorial(2) factorial(3) factorial(9) factorial(5)>
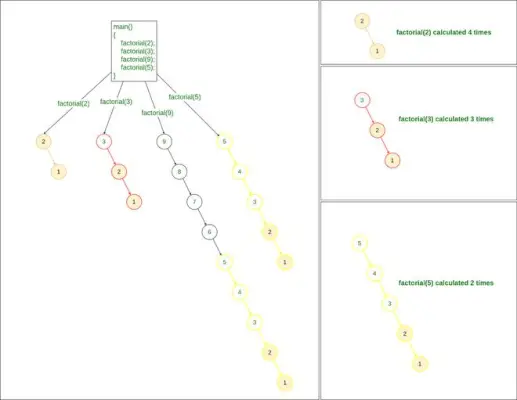
Méthode récursive pour trouver Factorial
Il est donc prudent de dire que pour trouver une factorielle de nombres K nombres, la complexité temporelle nécessaire sera O(N*K)
- SUR) pour trouver la factorielle d'un nombre particulier, et
- FLÈCHE) pour appeler la méthode factorial() K à des moments différents.
Comment la mémorisation peut-elle aider à résoudre de tels problèmes ?
Si l'on remarque dans le problème ci-dessus, lors du calcul factoriel de 9 :
clé du candidat
- Nous calculons la factorielle de 2
- Nous calculons également la factorielle de 3,
- et nous calculons également la factorielle de 5
Par conséquent, si nous stockons le résultat de chaque factorielle individuelle au premier moment du calcul, nous pouvons facilement renvoyer la factorielle de n'importe quel nombre requis en seulement un temps O(1). Ce processus est connu sous le nom Mémorisation .
Solution utilisant la mémorisation (Comment fonctionne la mémorisation ?) :
Si nous trouvons d'abord la factorielle de 9 et stockons les résultats des sous-problèmes individuels, nous pouvons facilement imprimer la factorielle de chaque entrée dans O(1).
Par conséquent, la complexité temporelle pour trouver des nombres factoriels à l’aide de la mémisation sera SUR)
- SUR) pour trouver la factorielle de la plus grande entrée
- O(1) pour imprimer la factorielle de chaque entrée.
Types de mémorisation
La mise en œuvre de la mémorisation dépend des paramètres changeants qui sont responsables de la résolution du problème. Il existe différentes dimensions de mise en cache qui sont utilisées dans la technique de mémorisation. Vous en trouverez ci-dessous quelques-unes :
- Mémisation 1D : Fonction récursive qui n'a qu'un seul argument dont la valeur n'était pas constante après chaque appel de fonction.
- Mémorisation 2D : La fonction récursive qui n'a que deux arguments dont la valeur n'était pas constante après chaque appel de fonction.
- Mémorisation 3D : La fonction récursive qui n'a que trois arguments dont les valeurs n'étaient pas constantes après chaque appel de fonction.
Comment la technique de mémorisation est utilisée en programmation dynamique ?
La programmation dynamique aide à résoudre efficacement les problèmes comportant des sous-problèmes qui se chevauchent et des propriétés de sous-structure optimales. L'idée derrière la programmation dynamique est de diviser le problème en sous-problèmes plus petits et de sauvegarder le résultat pour une utilisation future, éliminant ainsi le besoin de calculer le résultat à plusieurs reprises.
Il existe deux approches pour formuler une solution de programmation dynamique :
- Approche descendante : Cette approche suit la mémorisation technique . Cela consiste en récursivité et mise en cache . En calcul, la récursivité représente le processus d'appel répété de fonctions, tandis que le cache fait référence au processus de stockage des résultats intermédiaires.
- Une approche en profondeur: Cette approche utilise le tabulation technique pour mettre en œuvre la solution de programmation dynamique. Il répond aux mêmes problèmes que précédemment, mais sans récursion. Dans cette approche, l'itération remplace la récursivité. Par conséquent, il n’y a pas d’erreur de débordement de pile ni de surcharge des procédures récursives.
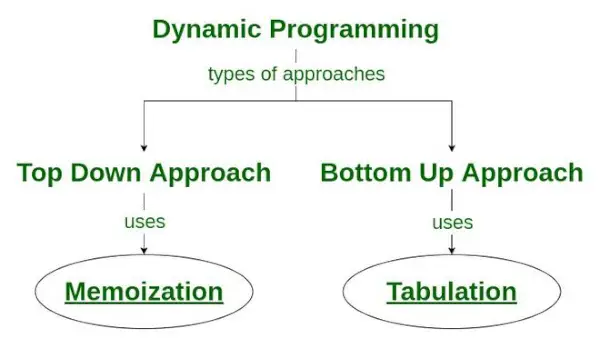
Comment la technique de mémorisation est utilisée dans la programmation dynamique
En quoi la mémorisation est-elle différente de la tabulation ?

Tabulation vs mémorisation
Pour plus de détails, veuillez consulter : Tabulation vs mémisation
Problèmes de pratique de codage sur la mémorisation
| Question | Article | Pratique | Vidéo |
|---|---|---|---|
| Comptez les chemins pour atteindre le nième escalier | Voir | Résoudre | Montre |
| Problème de coupure de mot | DP-32 | Voir | Résoudre | Montre |
| Programme pour les nombres de Fibonacci | Voir | Résoudre | Montre |
| nième numéro catalan | Voir | Résoudre | Montre |
| Problème de mine d'or | Voir | Résoudre | Montre |
| Problème de somme de sous-ensemble | Voir | Résoudre | Montre |
| Couper une tige | Voir | Résoudre | Montre |
| Chemin de coût minimum | Voir | Résoudre | Montre |
| Nombre minimum de sauts pour atteindre la fin | Voir | Résoudre | Montre |
| Sous-chaîne palindromique la plus longue | Ensemble 1 | Voir | Résoudre | Montre |
| Sous-séquence répétitive la plus longue | Voir | Résoudre | Montre |
| Comptez les chemins pour atteindre le nième escalier en utilisant l'étape 1, 2 ou 3 | Voir | Résoudre | Montre |
| Nombre de façons différentes d'exprimer N comme la somme de 1, 3 et 4 | Voir | Résoudre | Montre |
| Compter le nombre de façons de parcourir une distance | Voir | Résoudre | Montre |
| Nombre de tableaux ayant des éléments consécutifs avec des valeurs différentes | Voir | Résoudre | Montre |
| Sous-tableau contigu à la plus grande somme | Voir | Résoudre | Montre |
| Sous-tableau contigu à la plus petite somme | Voir | Résoudre | Montre |
| Chemins uniques dans une grille avec obstacles | Voir | Résoudre | Montre |
| Différentes façons de résumer n en utilisant des nombres supérieurs ou égaux à m | Voir | Résoudre | Montre |
Foire aux questions (FAQ) sur la mémorisation
1 : La mémorisation est-elle meilleure que le DP ?
La mémorisation est l'approche descendante pour résoudre un problème avec la programmation dynamique. C'est ce qu'on appelle la mémorisation car nous allons créer un mémo pour les valeurs renvoyées par la résolution de chaque problème.
2 : La mémorisation est-elle la même chose que la mise en cache ?
La mémorisation est en fait un type spécifique de mise en cache. Le terme mise en cache peut généralement faire référence à toute technique de stockage (comme la mise en cache HTTP) pour une utilisation future, mais la mémorisation fait plus spécifiquement référence à la fonction de mise en cache qui renvoie la valeur.
3 : Pourquoi la mémorisation est descendante ?
L’approche descendante divise le vaste problème en plusieurs sous-problèmes. si le sous-problème est déjà résolu, réutilisez la réponse. Sinon, résolvez le sous-problème et stockez le résultat dans une mémoire.
4 : La mémorisation utilise-t-elle la récursion ?
La mémorisation suit une approche descendante pour résoudre le problème. Il consiste en la récursivité et la mise en cache. En calcul, la récursivité représente le processus d'appel répété de fonctions, tandis que le cache fait référence au processus de stockage des résultats intermédiaires.
5 : Dois-je utiliser la tabulation ou la mémorisation ?
Pour les problèmes nécessitant la résolution de tous les sous-problèmes, la tabulation surpasse généralement la mémorisation d'un facteur constant. En effet, la tabulation n'a pas de surcharge de récursion, ce qui réduit le temps de résolution de la pile d'appels de récursion à partir de la mémoire de la pile.
Chaque fois qu'un sous-problème doit être résolu pour que le problème d'origine soit résolu, la mémorisation est préférable car un sous-problème est résolu paresseusement, c'est-à-dire que seuls les calculs requis sont effectués.
6 : Où la mémorisation est-elle utilisée ?
La mémorisation est une technique d'optimisation utilisée pour accélérer les programmes informatiques en mettant en cache les résultats d'appels de fonctions coûteux et en les renvoyant lorsque les mêmes entrées sont rencontrées à nouveau.
7 : Pourquoi cela s’appelle-t-on mémorisation ?
Le terme mémorisation vient du mot latin memorandum (se souvenir), qui est communément abrégé en mémo en anglais américain, et qui signifie transformer les résultats d'une fonction en quelque chose à retenir.
8 : Comment la mémorisation réduit-elle la complexité temporelle ?
Résoudre le même problème encore et encore prend du temps et augmente la complexité d'exécution de l'ensemble du programme. Ce problème peut être résolu en conservant un cache ou une mémoire où nous stockerons le résultat déjà calculé du problème pour une entrée particulière. Ainsi, si nous ne voulons pas recalculer le même problème, nous pouvons simplement utiliser le résultat stocké en mémoire et réduire la complexité temporelle.
9 : Quelle est la différence entre la mémorisation et la mise en cache ?
La mémorisation est en fait un type spécifique de mise en cache qui consiste à mettre en cache la valeur de retour d'une fonction basée sur l'entrée. La mise en cache est un terme plus général. Par exemple, la mise en cache HTTP est une mise en cache mais ce n'est pas une mémorisation.
10 : Pourquoi la tabulation est-elle plus rapide que la mémorisation ?
La tabulation est généralement plus rapide que la mémorisation, car elle est itérative et la résolution de sous-problèmes ne nécessite aucune surcharge d'appels récursifs.
La mémorisation est une technique utilisée en informatique pour accélérer l'exécution de fonctions récursives ou coûteuses en termes de calcul en mettant en cache les résultats des appels de fonction et en renvoyant les résultats mis en cache lorsque les mêmes entrées se reproduisent.
L'idée de base de la mémorisation est de stocker la sortie d'une fonction pour un ensemble d'entrées donné et de renvoyer le résultat mis en cache si la fonction est à nouveau appelée avec les mêmes entrées. Cette technique permet de gagner du temps de calcul, en particulier pour les fonctions appelées fréquemment ou présentant une complexité temporelle élevée.
Voici un guide étape par étape pour mettre en œuvre la mémorisation :
Identifiez la fonction que vous souhaitez optimiser à l'aide de la mémorisation. Cette fonction devrait avoir des calculs répétés et coûteux pour la même entrée.
Créez un objet dictionnaire pour stocker les résultats mis en cache de la fonction. Les clés du dictionnaire doivent être les paramètres d'entrée de la fonction et les valeurs doivent être les résultats calculés.
Au début de la fonction, vérifiez si les paramètres d'entrée sont déjà présents dans le dictionnaire du cache. Si tel est le cas, renvoyez le résultat mis en cache.
Si les paramètres d'entrée ne figurent pas dans le dictionnaire de cache, calculez le résultat et stockez-le dans le dictionnaire de cache avec les paramètres d'entrée comme clé.
Renvoie le résultat calculé.
Voici un exemple de code Python d'implémentation de la mémorisation à l'aide d'un dictionnaire :
Python3
def> fibonacci(n, cache>=>{}):> >if> n>in> cache:> >return> cache[n]> >if> n>=>=> 0>:> >result>=> 0> >elif> n>=>=> 1>:> >result>=> 1> >else>:> >result>=> fibonacci(n>->1>)>+> fibonacci(n>->2>)> >cache[n]>=> result> >return> result> |
>
liste chaînée
>Sortir
>
Dans le code ci-dessus, nous définissons une fonction appelée fibonacci qui calcule le nième nombre de la séquence de Fibonacci. Nous utilisons un objet dictionnaire appelé cache pour stocker les résultats des appels de fonction. Si le paramètre d'entrée n est déjà présent dans le dictionnaire du cache, nous renvoyons le résultat mis en cache. Sinon, nous calculons le résultat en utilisant des appels récursifs à la fonction fibonacci et le stockons dans le dictionnaire cache avant de le renvoyer.
La mémorisation peut être utilisée pour optimiser les performances de nombreuses fonctions nécessitant des calculs répétés et coûteux. En mettant en cache les résultats des appels de fonction, nous pouvons éviter les calculs inutiles et accélérer l'exécution de la fonction.
Conclusion
La mémorisation est un concept de programmation et peut être appliquée à n'importe quel langage de programmation. Son objectif absolu est d'optimiser le programme. Ce problème survient généralement lorsque les programmes effectuent des calculs lourds. Cette technique met en cache tous les résultats précédents calculés afin de ne pas avoir à recalculer pour le même problème.
Articles Liés:
- Mémisation à l'aide de décorateurs en Python
- Mémisation JavaScript
