La régression logistique dans la programmation R est un algorithme de classification utilisé pour trouver la probabilité de réussite et d'échec d'un événement. La régression logistique est utilisée lorsque la variable dépendante est de nature binaire (0/1, Vrai/Faux, Oui/Non). La fonction logit est utilisée comme fonction de lien dans une distribution binomiale.

La probabilité d’une variable de résultat binaire peut être prédite à l’aide de la technique de modélisation statistique connue sous le nom de régression logistique. Il est largement utilisé dans de nombreux secteurs différents, notamment le marketing, la finance, les sciences sociales et la recherche médicale.

La fonction logistique, communément appelée fonction sigmoïde, est l'idée de base qui sous-tend la régression logistique. Cette fonction sigmoïde est utilisée en régression logistique pour décrire la corrélation entre les variables prédictives et la probabilité du résultat binaire.

Régression logistique dans la programmation R

La régression logistique est également connue sous le nom de Régression logistique binomiale . Il est basé sur la fonction sigmoïde où la sortie est une probabilité et l'entrée peut aller de -infini à +infini.

Théorie

La régression logistique est également connue sous le nom de modèle linéaire généralisé. Puisqu'elle est utilisée comme technique de classification pour prédire une réponse qualitative, la valeur de y varie de 0 à 1 et peut être représentée par l'équation suivante :

Régression logistique dans la programmation R

p est la probabilité de la caractéristique d’intérêt. L’odds ratio est défini comme la probabilité de succès par rapport à la probabilité d’échec. Il s'agit d'une représentation clé des coefficients de régression logistique et peut prendre des valeurs comprises entre 0 et l'infini. Le rapport de cotes est de 1 lorsque la probabilité de succès est égale à la probabilité d’échec. Le rapport de cotes est de 2 lorsque la probabilité de succès est deux fois supérieure à la probabilité d’échec. Le rapport de cotes est de 0,5 lorsque la probabilité d’échec est deux fois supérieure à la probabilité de succès.

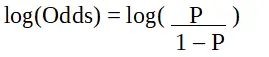
Régression logistique dans la programmation R

Puisque nous travaillons avec une distribution binomiale (variable dépendante), nous devons choisir une fonction de lien la mieux adaptée à cette distribution.

tri de tableau Java

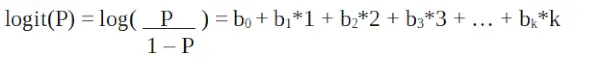
Régression logistique dans la programmation R

C'est un fonction de connexion . Dans l'équation ci-dessus, la parenthèse est choisie pour maximiser la probabilité d'observer les valeurs de l'échantillon plutôt que de minimiser la somme des erreurs quadratiques (comme la régression ordinaire). Le logit est également connu sous le nom de journal des cotes. La fonction logit doit être liée linéairement aux variables indépendantes. Cela vient de l’équation A, où le membre de gauche est une combinaison linéaire de x. Ceci est similaire à l’hypothèse OLS selon laquelle y est linéairement lié à x. Les variables b0, b1, b2…etc sont inconnues et doivent être estimées sur les données d'entraînement disponibles. Dans un modèle de régression logistique, multiplier b1 par une unité modifie le logit de b0. Les changements P dus à un changement d'une unité dépendront de la valeur multipliée. Si b1 est positif alors P augmentera et si b1 est négatif alors P diminuera.

L'ensemble de données

voitures mt (essai routier de voiture Motor Trend) comprend la consommation de carburant, les performances et 10 aspects de la conception automobile pour 32 automobiles. Il est préinstallé avec dplyr paquet dans R.

R.

>

renvoyer un tableau java

>

Effectuer une régression logistique sur un ensemble de données

La régression logistique est implémentée dans R en utilisant glm() en entraînant le modèle à l'aide de fonctionnalités ou de variables dans l'ensemble de données.

R.

>

>

Fractionner les données

R.

>

>

Sortir:

comment renvoyer un tableau en Java

Call: glm(formula = vs ~ wt + disp, family = 'binomial', data = train_reg) Deviance Residuals: Min 1Q Median 3Q Max -1.6552 -0.4051 0.4446 0.6180 1.9191 Coefficients: Estimate Std. Error z value Pr(>|z|) (Interception) 1,58781 2,60087 0,610 0,5415 poids 1,36958 1,60524 0,853 0,3936 disp -0,02969 0,01577 -1,882 0,0598 . --- Signif. codes : 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 ' ' 1 (Paramètre de dispersion pour la famille binomiale pris à 1) Déviance nulle : 34,617 sur 24 degrés de liberté Déviance résiduelle : 20,212 sur 22 degrés de liberté AIC : 26,212 Nombre d'itérations de Fisher Scoring : 6>

Appel : l'appel de fonction utilisé pour ajuster le modèle de régression logistique est affiché, ainsi que des informations sur la famille, la formule et les données. Résidus de déviance : ce sont les résidus de déviance, qui évaluent le degré d’ajustement du modèle. Ils représentent les écarts entre les réponses réelles et la probabilité prédite par le modèle de régression logistique. Coefficients : ces coefficients de régression logistique représentent les cotes ou logit de la variable de réponse. Les erreurs types liées aux coefficients estimés sont présentées dans la norme Std. Colonne d'erreur. Codes de signification : le niveau de signification de chaque variable prédictive est indiqué par les codes de signification. Paramètre de dispersion : dans la régression logistique, le paramètre de dispersion sert de paramètre d'échelle pour la distribution binomiale. Il est défini sur 1 dans ce cas, indiquant que la dispersion supposée est de 1. Déviance nulle : La déviance nulle calcule l'écart du modèle lorsque seule l'ordonnée à l'origine est prise en compte. Il symbolise l’écart qui résulterait d’un modèle sans prédicteurs. Déviance résiduelle : la déviance résiduelle calcule l’écart du modèle une fois les prédicteurs ajustés. Il représente l’écart résiduel après prise en compte des prédicteurs. AIC : le critère d'information d'Akaike (AIC), qui prend en compte le nombre de prédicteurs, est une mesure de l'adéquation d'un modèle. Il pénalise les modèles plus complexes afin d'éviter le surajustement. Les modèles mieux adaptés sont indiqués par des valeurs AIC plus faibles. Nombre d'itérations de notation de Fisher : le nombre d'itérations nécessaires à la procédure de notation de Fisher pour estimer les paramètres du modèle est indiqué par le nombre d'itérations.

Prédire les données de test en fonction du modèle

R.

>

>

Sortir:

Hornet Sportabout Merc 280C Merc 450SE Chrysler Imperial 0.01226166 0.78972164 0.26380531 0.01544309 AMC Javelin Camaro Z28 Ford Pantera L 0.06104267 0.02807992 0.01107943>

R.

>

>

Sortir:

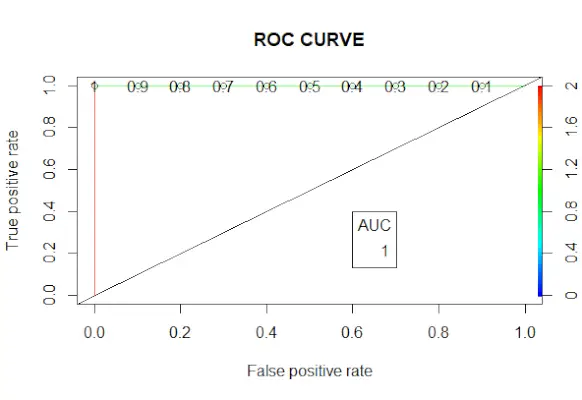
Courbe ROC

Exemple 2 :

Nous pouvons effectuer un modèle de régression logistique Titanic Data défini dans R.

R.

comment déréférencer un pointeur en c

tutoriel hadoop

>

>

Sortir:

Call: glm(formula = Survived ~ Class + Sex + Age, family = binomial, data = data) Deviance Residuals: Min 1Q Median 3Q Max -1.177 -1.177 0.000 1.177 1.177 Coefficients: Estimate Std. Error z value Pr(>|z|) (Interception) 4.022e-16 8.660e-01 0 1 Classe 2ème -9.762e-16 1.000e+00 0 1 Classe 3ème -4.699e-16 1.000e+00 0 1 ClasseCrew -5.551e-16 1.000e+ 00 0 1 SexFemale -3.140e-16 7.071e-01 0 1 AgeAdult 5.103e-16 7.071e-01 0 1 (Paramètre de dispersion pour la famille binomiale pris à 1) Déviance nulle : 44,361 sur 31 degrés de liberté Déviance résiduelle : 44,361 sur 26 degrés de liberté AIC : 56,361 Nombre d'itérations Fisher Scoring : 2>

Tracez la courbe ROC pour l'ensemble de données Titanic

R.

>

>

Sortir:

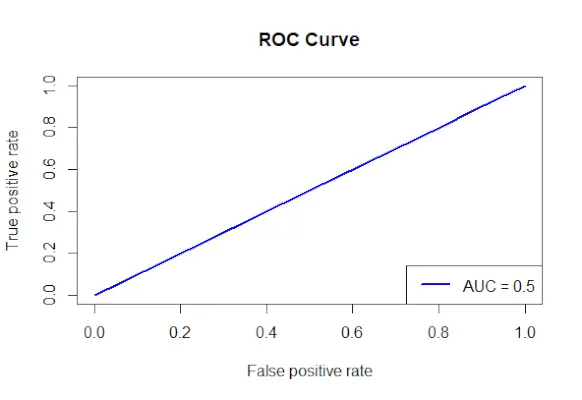
Courbe ROC

• Les facteurs utilisés pour prédire la survie sont spécifiés et la formule Classe de survie + Sexe + Âge est utilisée pour créer un modèle de régression logistique.
• À l'aide de la fonction prédire(), des prédictions sont faites sur l'ensemble de données à l'aide du modèle ajusté.
• Les probabilités projetées sont combinées avec les valeurs de résultat réelles pour créer un objet de prédiction à l'aide de la méthode prédiction() du package ROCR.
• La mesure du taux de vrais positifs (tpr) et la mesure sur l'axe des x du taux de faux positifs (fpr) sont spécifiées, et un objet courbe ROC est créé à l'aide de la fonction performance() du package ROCR.
• L'objet courbe ROC (roc_obj), qui spécifie le titre principal, la couleur et la largeur de ligne, est tracé à l'aide de la fonction plot().
• Il utilise la fonction performance() avec Measure = auc pour déterminer la valeur AUC (aire sous la courbe) et ajoute des étiquettes et une légende au tracé.