Arbre de recherche binaire est une structure de données utilisée en informatique pour organiser et stocker des données de manière triée. L'arbre de recherche binaire suit toutes les propriétés de l'arbre binaire et ses gauche l'enfant contient des valeurs inférieures au nœud parent et le droite l'enfant contient des valeurs supérieures à celles du nœud parent. Cette structure hiérarchique permet une gestion efficace Recherche , Insertion , et Effacement opérations sur les données stockées dans l’arborescence.
Arbre de recherche binaire
Table des matières
vlc pour télécharger des vidéos youtube
- Qu’est-ce que l’arbre de recherche binaire ?
- Propriétés de l'arbre de recherche binaire
- Gestion des valeurs en double dans l'arborescence de recherche binaire
- Opérations effectuées sur un BST
- 1. Recherche d'un nœud dans BST
- 2. Insérez un nœud dans un BST
- 3. Supprimer un nœud de BST
- 4. Traversée (traversée dans l'ordre de BST)
- Applications de la BST
- Avantages
- Désavantages
- FAQ (questions fréquemment posées) sur l'arbre de recherche binaire :
Qu’est-ce que l’arbre de recherche binaire ?
Arbre de recherche binaire (BST) est un type particulier de arbre binaire dans lequel l'enfant gauche d'un nœud a une valeur inférieure à la valeur du nœud et l'enfant droit a une valeur supérieure à la valeur du nœud. Cette propriété est appelée propriété BST et permet de rechercher, d'insérer et de supprimer efficacement des éléments dans l'arborescence.
Propriétés de l'arbre de recherche binaire :
- Le sous-arbre gauche d'un nœud contient uniquement des nœuds avec des clés inférieures à la clé du nœud.
- Le sous-arbre droit d'un nœud contient uniquement des nœuds dont les clés sont supérieures à la clé du nœud.
- Cela signifie que tout ce qui se trouve à gauche de la racine est inférieur à la valeur de la racine et tout ce qui se trouve à droite de la racine est supérieur à la valeur de la racine. Grâce à ces performances, une recherche binaire est très simple.
- Les sous-arbres gauche et droit doivent chacun également être un arbre de recherche binaire.
- Il ne doit pas y avoir de nœuds en double (BST peut avoir des valeurs en double avec différentes approches de gestion)
Gestion des valeurs en double dans l'arborescence de recherche binaire :
- Nous devons suivre un processus cohérent tout au long, c'est-à-dire soit stocker la valeur en double à gauche, soit stocker la valeur en double à droite de la racine, mais être cohérent avec votre approche.
Opérations de base sur l'arbre de recherche binaire :
1. Recherche d'un nœud dans BST :
Rechercher dans BST signifie localiser un nœud spécifique dans la structure de données. Dans l'arbre de recherche binaire, la recherche d'un nœud est facile en raison de son ordre spécifique. Les étapes de recherche d'un nœud dans l'arborescence de recherche binaire sont répertoriées comme suit :
- Commencez par comparer l’élément à rechercher avec l’élément racine de l’arborescence.
- Si root correspond à l’élément cible, renvoie l’emplacement du nœud.
- S'il ne correspond pas, vérifiez si l'élément est inférieur à l'élément racine, s'il est plus petit que l'élément racine, puis déplacez-vous vers le sous-arbre de gauche.
- S'il est plus grand que l'élément racine, déplacez-vous vers le sous-arbre de droite.
- Répétez la procédure ci-dessus de manière récursive jusqu'à ce que la correspondance soit trouvée.
- Si l'élément n'est pas trouvé ou n'est pas présent dans l'arborescence, retournez NULL.
Maintenant, comprenons la recherche dans l'arbre binaire à l'aide d'un exemple :
Ci-dessous est donné un BST et nous devons rechercher l'élément 6.
File d'attente de priorité
Code:
Vous trouverez ci-dessous l'implémentation de la recherche dans BST :
C++ // C++ function to search a given key in a given BST #include using namespace std; struct node { int key; struct node *left, *right; }; // A utility function to create a new BST node struct node* newNode(int item) { struct node* temp = new struct node; temp->clé = élément ; temp->gauche = temp->droite = NULL ; température de retour ; } // Une fonction utilitaire pour insérer // un nouveau nœud avec une clé donnée dans BST struct node* insert(struct node* node, int key) { // Si l'arborescence est vide, renvoie un nouveau nœud if (node == NULL ) return newNode(clé); // Sinon, répétez l'arborescence if (clé< node->clé) nœud->gauche = insert(nœud->gauche, clé); sinon if (key> node->key) node->right = insert(node->right, key); // Renvoie le pointeur de nœud (inchangé) return node; } // Fonction utilitaire pour rechercher une clé dans une structure BST node* search(struct node* root, int key) root->key == key) return root; // La clé est supérieure à la clé de root si (root->key< key) return search(root->droite, clé); // La clé est plus petite que la clé de root return search(root->left, key);> C // C function to search a given key in a given BST #include #include struct node { int key; struct node *left, *right; }; // A utility function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc(sizeof(struct node)); temp->clé = élément ; temp->gauche = temp->droite = NULL ; température de retour ; } // Une fonction utilitaire pour insérer // un nouveau nœud avec une clé donnée dans BST struct node* insert(struct node* node, int key) { // Si l'arborescence est vide, renvoie un nouveau nœud if (node == NULL ) return newNode(clé); // Sinon, récurrence dans l'arborescence if (clé< node->clé) nœud->gauche = insert(nœud->gauche, clé); sinon if (key> node->key) node->right = insert(node->right, key); // Renvoie le pointeur de nœud (inchangé) return node; } // Fonction utilitaire pour rechercher une clé dans une recherche BST struct node* (struct node* root, int key)> Java // Java program to search a given key in a given BST class Node { int key; Node left, right; public Node(int item) { key = item; left = right = null; } } class BinarySearchTree { Node root; // Constructor BinarySearchTree() { root = null; } // A utility function to insert // a new node with given key in BST Node insert(Node node, int key) { // If the tree is empty, return a new node if (node == null) { node = new Node(key); return node; } // Otherwise, recur down the tree if (key < node.key) node.left = insert(node.left, key); else if (key>node.key) node.right = insert(node.right, clé); // Renvoie le pointeur de nœud (inchangé) return node; } // Fonction utilitaire pour rechercher une clé dans une recherche de nœud BST (racine du nœud, clé int) // Cas de base : la racine est nulle ou la clé est présente à la racine si (root == null> Python # Python3 function to search a given key in a given BST class Node: # Constructor to create a new node def __init__(self, key): self.key = key self.left = None self.right = None # A utility function to insert # a new node with the given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return Node(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Renvoie le nœud de retour du pointeur de nœud (inchangé) # Fonction utilitaire pour rechercher une clé dans une recherche de définition BST (root, key) : # Cas de base : root is null ou la clé est présente à la racine si la racine est None ou root.key == clé : retourner la racine # La clé est supérieure à la clé de la racine si root.key< key: return search(root.right, key) # Key is smaller than root's key return search(root.left, key)>
Javascript // Javascript function to search a given key in a given BST class Node { constructor(key) { this.key = key; this.left = null; this.right = null; } } // A utility function to insert // a new node with given key in BST function insert(node, key) { // If the tree is empty, return a new node if (node === null) { return new Node(key); } // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>node.key) { node.right = insert(node.right, clé); } // Renvoie le pointeur de nœud (inchangé) return node; } // Fonction utilitaire pour rechercher une clé dans une fonction BST search(root, key) { // Cas de base : la racine est nulle ou la clé est présente à la racine if (root === null || root.key === key ) { retourner la racine ; } // La clé est supérieure à la clé de root si (root.key< key) { return search(root.right, key); } // Key is smaller than root's key return search(root.left, key); }>
2. Insérer un nœud dans un BST :
Une nouvelle clé est toujours insérée au niveau du vantail. Commencez à rechercher une clé depuis la racine jusqu'à un nœud feuille. Une fois qu'un nœud feuille est trouvé, le nouveau nœud est ajouté en tant qu'enfant du nœud feuille.
Code:
Vous trouverez ci-dessous l'implémentation de l'insertion d'un seul nœud dans l'arbre de recherche binaire :
C++ // Given Node Structure struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->clé = élément ; temp->gauche = temp->droite = NULL ; température de retour ; } // Fonction pour insérer un nouveau nœud avec // une clé donnée dans BST struct node* insert(struct node* node, int key) { // Si l'arborescence est vide, renvoie un nouveau nœud if (node == NULL) return nouveauNoeud(clé); // Sinon, récurrence dans l'arborescence if (clé< node->clé) { nœud->gauche = insert (nœud->gauche, clé); } else if (key> node->key) { node->right = insert(node->right, key); } // Renvoie le pointeur de nœud return node; }> C // Given Node Structure struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->clé = élément ; temp->gauche = temp->droite = NULL ; température de retour ; } // Fonction pour insérer un nouveau nœud avec // une clé donnée dans BST struct node* insert(struct node* node, int key) { // Si l'arborescence est vide, renvoie un nouveau nœud if (node == NULL) return nouveauNoeud(clé); // Sinon, récurrence dans l'arborescence if (clé< node->clé) { nœud->gauche = insert (nœud->gauche, clé); } else if (key> node->key) { node->right = insert(node->right, key); } // Renvoie le pointeur de nœud return node; }> Java class GFG { // Given Node Structure static class node { int key; node left, right; }; // Function to create a new BST node static node newNode(int item) { node temp = new node(); temp.key = item; temp.left = temp.right = null; return temp; } // Function to insert a new node with // given key in BST static node insert(node node, int key) { // If the tree is empty, return a new node if (node == null) return newNode(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>node.key) { node.right = insert(node.right, clé); } // Renvoie le nœud return node; } }> Python3 # Given Node Structure class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to insert a new node with # given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return Node(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Renvoie le pointeur de nœud return node>
Javascript // Given Node Structure class Node { constructor(key){ this.key = key; this.left = null; this.right = null; } } // Function to insert a new node with // given key in BST function insert(node, key) { // If the tree is empty, return a new node if (node == null) return new Node(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>node.key) { node.right = insert(node.right, clé); } // Renvoie le pointeur de nœud return node; }> Complexité temporelle : O(N), où N est le nombre de nœuds du BST
Espace auxiliaire : O(1)
3. Supprimer un nœud de BST :
Il est utilisé pour supprimer un nœud avec une clé spécifique du BST et renvoyer le nouveau BST.
Différents scénarios de suppression du nœud :
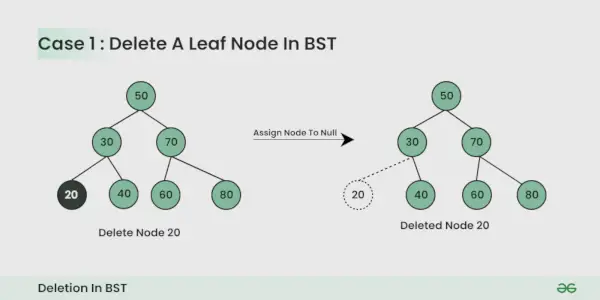
Le nœud à supprimer est le nœud feuille :
C'est simple, vous pouvez simplement l'annuler.
statique en c
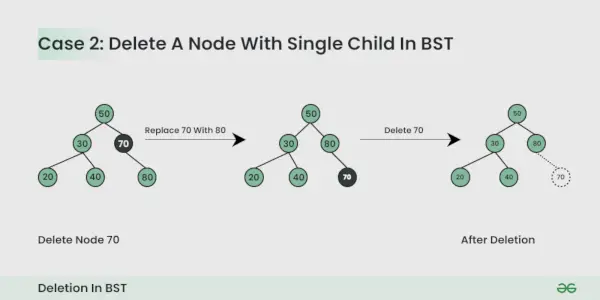
Le nœud à supprimer a un enfant :
Vous pouvez simplement remplacer le nœud par le nœud enfant.
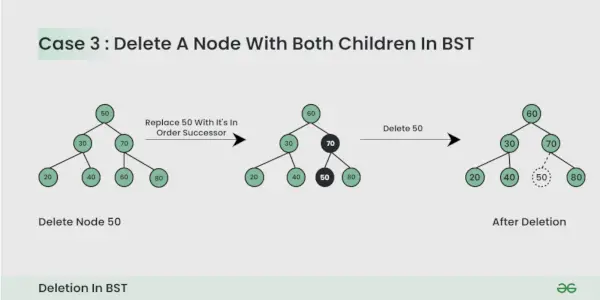
Le nœud à supprimer a deux enfants :
Ici, nous devons supprimer le nœud est de telle manière que l'arborescence résultante suive les propriétés d'un BST. L'astuce consiste à trouver le successeur dans l'ordre du nœud. Copiez le contenu du successeur inorder sur le nœud et supprimez le successeur inorder.
Prenez soin des éléments suivants lors de la suppression d'un nœud d'un BST :
- Il faut déterminer quel sera le remplacement du nœud à supprimer.
- Vous souhaitez une perturbation minimale de la structure arborescente existante
- Peut prendre le nœud de remplacement du sous-arbre gauche ou droit des nœuds supprimés.
- Si nous prenons if dans le sous-arbre de gauche, nous devons prendre la plus grande valeur du sous-arbre de gauche.
- Si nous prenons if dans le sous-arbre de droite, nous devons prendre la plus petite valeur dans le sous-arbre de droite.
Code:
Ci-dessous l'implémentation de la suppression dans BST :
C++ // C++ program to delete // a node of BST // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->clé = élément ; temp->gauche = temp->droite = NULL ; température de retour ; } // Fonction pour insérer un nouveau nœud avec // une clé donnée dans BST struct node* insert(struct node* node, int key) { // Si l'arborescence est vide, renvoie un nouveau nœud if (node == NULL) return nouveauNoeud(clé); // Sinon, répétez l'arborescence if (clé< node->clé) { nœud->gauche = insert (nœud->gauche, clé); } else if (key> node->key) { node->right = insert(node->right, key); } // Renvoie le pointeur de nœud return node; } // Fonction qui renvoie le nœud avec // la valeur de clé minimale trouvée dans cet arbre struct node* minValueNode(struct node* node) { struct node* current = node; // Boucle vers le bas pour trouver la feuille la plus à gauche while (current && current->left != NULL) current = current->left; courant de retour ; } // Fonction qui supprime la clé et // renvoie la nouvelle racine struct node* deleteNode(struct node* root, int key) { // cas de base if (root == NULL) return root; // Si la clé à supprimer est // plus petite que la clé de la racine, // alors elle se trouve dans le sous-arbre gauche if (key< root->clé) { racine->gauche = deleteNode(racine->gauche, clé); } // Si la clé à supprimer est // supérieure à la clé de la racine, // alors elle se trouve dans le sous-arbre droit sinon if (key> root->key) { root->right = deleteNode(root-> droite, clé); } // Si la clé est la même que celle de root, // alors c'est le nœud // à supprimer else { // Nœud avec un seul enfant // ou aucun enfant if (root->left == NULL) { struct node* temp = root->right ; gratuit(racine); température de retour ; } else if (root->right == NULL) { struct node* temp = root->left; gratuit(racine); température de retour ; } // Nœud avec deux enfants : // Récupère le successeur dans l'ordre (le plus petit // dans le sous-arbre de droite) struct node* temp = minValueNode(root->right); // Copiez le contenu // du successeur de l'ordre dans ce nœud root->key = temp->key; // Supprime le successeur dans l'ordre root->right = deleteNode(root->right, temp->key); } renvoie la racine ; }> C // C program to delete // a node of BST // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->clé = élément ; temp->gauche = temp->droite = NULL ; température de retour ; } // Fonction pour insérer un nouveau nœud avec // une clé donnée dans BST struct node* insert(struct node* node, int key) { // Si l'arborescence est vide, renvoie un nouveau nœud if (node == NULL) return nouveauNoeud(clé); // Sinon, récurrence dans l'arborescence if (clé< node->clé) { nœud->gauche = insert (nœud->gauche, clé); } else if (key> node->key) { node->right = insert(node->right, key); } // Renvoie le pointeur de nœud return node; } // Fonction qui renvoie le nœud avec // la valeur de clé minimale trouvée dans cet arbre struct node* minValueNode(struct node* node) { struct node* current = node; // Boucle vers le bas pour trouver la feuille la plus à gauche while (current && current->left != NULL) current = current->left; courant de retour ; } // Fonction qui supprime la clé et // renvoie la nouvelle racine struct node* deleteNode(struct node* root, int key) { // cas de base if (root == NULL) return root; // Si la clé à supprimer est // plus petite que la clé de la racine, // alors elle se trouve dans le sous-arbre gauche if (key< root->clé) { racine->gauche = deleteNode(racine->gauche, clé); } // Si la clé à supprimer est // supérieure à la clé de la racine, // alors elle se trouve dans le sous-arbre droit sinon if (key> root->key) { root->right = deleteNode(root-> droite, clé); } // Si la clé est la même que celle de root, // alors c'est le nœud // à supprimer else { // Nœud avec un seul enfant // ou aucun enfant if (root->left == NULL) { struct node* temp = root->right ; gratuit(racine); température de retour ; } else if (root->right == NULL) { struct node* temp = root->left; gratuit(racine); température de retour ; } // Nœud avec deux enfants : // Récupère le successeur dans l'ordre (le plus petit // dans le sous-arbre de droite) struct node* temp = minValueNode(root->right); // Copiez le contenu // du successeur de l'ordre dans ce nœud root->key = temp->key; // Supprime le successeur dans l'ordre root->right = deleteNode(root->right, temp->key); } renvoie la racine ; }> Java // Java program for Delete a Node of BST class GFG { // Given Node node static class node { int key; node left, right; }; // Function to create a new BST node static node newNode(int item) { node temp = new node(); temp.key = item; temp.left = temp.right = null; return temp; } // Function to insert a new node with // given key in BST static node insert(node node, int key) { // If the tree is empty, return a new node if (node == null) return newNode(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>node.key) { node.right = insert(node.right, clé); } // Renvoie le nœud return node; } // Fonction qui renvoie le nœud avec // la valeur de clé minimale trouvée dans cet arbre nœud statique minValueNode(node node) { node current = node; // Boucle vers le bas pour trouver la feuille la plus à gauche while (current != null && current.left != null) current = current.left; courant de retour ; } // Fonction qui supprime la clé et // renvoie le nouveau nœud statique racine deleteNode(node root, int key) { // Cas de base if (root == null) return root; // Si la clé à supprimer est // plus petite que la clé de la racine, // alors elle se trouve dans le sous-arbre gauche if (key< root.key) { root.left = deleteNode(root.left, key); } // If the key to be deleted is // greater than the root's key, // then it lies in right subtree else if (key>root.key) { root.right = deleteNode(root.right, clé); } // Si la clé est la même que celle de root, // alors c'est le nœud // à supprimer else { // Nœud avec un seul enfant // ou aucun enfant if (root.left == null) { nœud temp = root.right ; température de retour ; } else if (root.right == null) { node temp = root.left; température de retour ; } // Nœud avec deux enfants : // Récupère le successeur dans l'ordre (le plus petit // dans le sous-arbre de droite) node temp = minValueNode(root.right); // Copiez le contenu // du successeur de l'ordre sur ce nœud root.key = temp.key; // Supprime le successeur de l'ordre root.right = deleteNode(root.right, temp.key); } renvoie la racine ; }> Python # Python program to delete a node of BST # Given Node node class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to insert a new node with # given key in BST def insert(root, key): # If the tree is empty, return a new node if root is None: return Node(key) # Otherwise, recur down the tree if key < root.key: root.left = insert(root.left, key) elif key>root.key: root.right = insert(root.right, key) # Renvoie le pointeur de nœud return root # Fonction pour effectuer un parcours dans l'ordre de BST def inorder(root): if root: inorder(root.left) print(root. key, end=' ') inorder(root.right) # Fonction qui renvoie le nœud avec la valeur de clé minimale # trouvée dans cet arbre def minValueNode(node): current = node # Boucle vers le bas pour trouver la feuille la plus à gauche pendant qu'elle est actuelle et current.left n'est pas Aucun : current = current.left return current # Fonction qui supprime la clé et # renvoie la nouvelle racine def deleteNode(root, key) : # cas de base si root est None : return root # Si la clé doit être supprimé est # plus petit que la clé de la racine, # alors il se trouve dans le sous-arbre gauche si la clé< root.key: root.left = deleteNode(root.left, key) # If the key to be deleted is # greater than the root's key, # then it lies in right subtree elif key>root.key: root.right = deleteNode(root.right, key) # Si la clé est la même que celle de root, # alors c'est le nœud # à supprimer sinon : # Nœud avec un seul enfant # ou aucun enfant si root.left est None : temp = root.right root = None return temp elif root.right is None : temp = root.left root = None return temp # Nœud avec deux enfants : # Récupère le successeur dans l'ordre (le plus petit # dans le sous-arbre droit) temp = minValueNode(root.right) # Copiez le contenu du successeur de l'ordre # sur ce nœud root.key = temp.key # Supprimez le successeur de l'ordre root.right = deleteNode(root.right, temp.key) retourner la racine>
4. Traversée (traversée dans l'ordre de BST) :
Dans le cas des arbres de recherche binaires (BST), le parcours Inorder donne les nœuds dans un ordre non décroissant. Nous visitons d'abord l'enfant de gauche, puis la racine, et enfin l'enfant de droite.
Vous trouverez ci-dessous l'implémentation de la façon de parcourir dans l'ordre un arbre de recherche binaire :
C++ // C++ program to implement // inorder traversal of BST #include using namespace std; // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->clé = élément ; temp->gauche = temp->droite = NULL ; température de retour ; } // Fonction pour insérer un nouveau nœud avec // une clé donnée dans BST struct node* insert(struct node* node, int key) { // Si l'arborescence est vide, renvoie un nouveau nœud if (node == NULL) return nouveauNoeud(clé); // Sinon, récurrence dans l'arborescence if (clé< node->clé) { nœud->gauche = insert (nœud->gauche, clé); } else if (key> node->key) { node->right = insert(node->right, key); } // Renvoie le pointeur de nœud return node; } // Fonction pour effectuer un parcours dans l'ordre de BST void inorder(struct node* root) { if (root != NULL) { inorder(root->left); cout<< ' ' << root->clé; dans l'ordre (racine-> droite); } } // Driver Code int main() { /* Créons les éléments suivants BST 50 / 30 70 / / 20 40 60 80 */ struct node* root = NULL; // Création de la racine BST = insert(root, 50); insert(racine, 30); insert(racine, 20); insert(racine, 40); insert(racine, 70); insert(racine, 60); insert(racine, 80); // Appel de fonction order(root); renvoie 0 ; } // Ce code est contribué par shivanisinghss2110> C // C program to implement // inorder traversal of BST #include #include // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->clé = élément ; temp->gauche = temp->droite = NULL ; température de retour ; } // Fonction pour insérer un nouveau nœud avec // une clé donnée dans BST struct node* insert(struct node* node, int key) { // Si l'arborescence est vide, renvoie un nouveau nœud if (node == NULL) return nouveauNoeud(clé); // Sinon, répétez l'arborescence if (clé< node->clé) { nœud->gauche = insert (nœud->gauche, clé); } else if (key> node->key) { node->right = insert(node->right, key); } // Renvoie le pointeur de nœud return node; } // Fonction pour effectuer un parcours dans l'ordre de BST void inorder(struct node* root) { if (root != NULL) { inorder(root->left); printf('%d ', racine->clé); dans l'ordre (racine-> droite); } } // Driver Code int main() { /* Créons les éléments suivants BST 50 / 30 70 / / 20 40 60 80 */ struct node* root = NULL; // Création de la racine BST = insert(root, 50); insert(racine, 30); insert(racine, 20); insert(racine, 40); insert(racine, 70); insert(racine, 60); insert(racine, 80); // Appel de fonction order(root); renvoie 0 ; }> Java import java.io.*; // Java program for Inorder Traversal class GFG { // Given Node node static class node { int key; node left, right; }; // Function to create a new BST node static node newNode(int item) { node temp = new node(); temp.key = item; temp.left = temp.right = null; return temp; } // Function to insert a new node with // given key in BST static node insert(node node, int key) { // If the tree is empty, return a new node if (node == null) return newNode(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>node.key) { node.right = insert(node.right, clé); } // Renvoie le nœud return node; } // Fonction pour effectuer un parcours dans l'ordre de BST static void inorder(node root) { if (root != null) { inorder(root.left); System.out.print(' ' + root.key); dans l'ordre (root.right); } } // Code du pilote public static void main(String[] args) { /* Créons le BST suivant 50 / 30 70 / / 20 40 60 80 */ node root = null; // insertion de la valeur 50 root = insert(root, 50); // insertion de la valeur 30 insert(root, 30); // insertion de la valeur 20 insert(root, 20); // insertion de la valeur 40 insert(root, 40); // insertion de la valeur 70 insert(root, 70); // insertion de la valeur 60 insert(root, 60); // insertion de la valeur 80 insert(root, 80); // affiche l'ordre BST (root); } } // Ce code est fourni par abhijitjadhav1998> Python3 # Python program to implement # inorder traversal of BST # Given Node node class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to create a new BST node def newNode(item): temp = Node(item) temp.key = item temp.left = temp.right = None return temp # Function to insert a new node with # given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return newNode(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Renvoie le pointeur de nœud return node # Fonction pour effectuer un parcours dans l'ordre de BST def inorder(root): if root: inorder(root.left) print(root. key, end=' ') inorder(root.right) # Code du pilote si __name__ == '__main__' : # Créons le BST suivant # 50 # / # 30 70 # / / # 20 40 60 80 root = Aucun # Création du BST root = insert(root, 50) insert(root, 30) insert(root, 20) insert(root, 40) insert(root, 70) insert(root, 60) insert(root , 80) # Appel de fonction inorder(root) #Ce code est contribué par japmeet01>
Sortir
20 30 40 50 60 70 80>
Complexité temporelle : O(N), où N est le nombre de nœuds du BST
Espace auxiliaire : O(1)
différence entre l'arbre binaire et l'arbre de recherche binaire
Applications de la BST :
- Algorithmes graphiques : Les BST peuvent être utilisés pour implémenter des algorithmes graphiques, comme dans les algorithmes d'arbre couvrant minimum.
- Files d'attente prioritaires : Les BST peuvent être utilisés pour implémenter des files d'attente prioritaires, dans lesquelles l'élément ayant la priorité la plus élevée se trouve à la racine de l'arborescence et les éléments ayant une priorité inférieure sont stockés dans les sous-arbres.
- Arbre de recherche binaire auto-équilibré : Les BST peuvent être utilisés comme structures de données auto-équilibrées telles que l'arborescence AVL et l'arborescence rouge-noir.
- Stockage et récupération de données : Les BST peuvent être utilisés pour stocker et récupérer rapidement des données, par exemple dans des bases de données, où la recherche d'un enregistrement spécifique peut être effectuée en temps logarithmique.
Avantages :
- Recherche rapide : La recherche d'une valeur spécifique dans un BST a une complexité temporelle moyenne de O (log n), où n est le nombre de nœuds dans l'arborescence. C'est beaucoup plus rapide que de rechercher un élément dans un tableau ou une liste chaînée, qui ont une complexité temporelle de O(n) dans le pire des cas.
- Parcours dans l'ordre : Les BST peuvent être parcourus dans l'ordre, ce qui visite le sous-arbre gauche, la racine et le sous-arbre droit. Cela peut être utilisé pour trier un ensemble de données.
- Efficacité de l'espace : Les BST sont économes en espace car ils ne stockent aucune information redondante, contrairement aux tableaux et aux listes chaînées.
Désavantages:
- Arbres de travers : Si un arbre devient asymétrique, la complexité temporelle des opérations de recherche, d'insertion et de suppression sera O(n) au lieu de O(log n), ce qui peut rendre l'arbre inefficace.
- Temps supplémentaire requis : Les arbres auto-équilibrés nécessitent un temps supplémentaire pour maintenir l’équilibre pendant les opérations d’insertion et de suppression.
- Efficacité: Les BST ne sont pas efficaces pour les ensembles de données comportant de nombreux doublons, car ils gaspilleront de l'espace.
FAQ(Questions fréquemment posées)sur l'arbre de recherche binaire :
1. Qu'est-ce qu'un arbre de recherche binaire ?
Un arbre de recherche binaire (BST) est un arbre binaire où chaque nœud du sous-arbre de gauche est inférieur à la racine et chaque nœud du sous-arbre de droite a une valeur supérieure à la racine . Les propriétés d'un arbre de recherche binaire sont récursives : si l'on considère n'importe quel nœud comme racine, ces propriétés resteront vraies.
2. Qu'est-ce que l'opération d'arbre de recherche binaire ?
Il existe trois opérations principales dans l'arbre de recherche binaire : 1. Insertion, 2. Suppression, 3. Recherche. En raison de ses propriétés, il est efficace pour rechercher n'importe quel élément dans l'arbre de recherche binaire.
3. Qu'est-ce que l'arbre de recherche binaire et l'arbre AVL ?
Arbre de recherche binaire : Un arbre de recherche binaire (BST) est un arbre binaire dans lequel chaque nœud du sous-arbre de gauche est inférieur à la racine et chaque nœud du sous-arbre de droite a une valeur supérieure à la racine.
Arbre AVL : Les arbres de recherche binaires (BST) qui s'auto-équilibrent et tournent automatiquement sont appelés arbres AVL.
4. Quelles sont les utilisations de l’arbre de recherche binaire ?
Les arbres de recherche binaires peuvent être utilisés pour implémenter des types de données abstraits tels que ensembles dynamiques, tables de recherche et files d'attente prioritaires, et utilisé dans algorithmes de tri comme le tri des arbres.
5. Quelle est la différence entre un arbre de recherche binaire et un arbre binaire ?
Un arbre de recherche binaire est un arbre qui suit un certain ordre pour organiser les éléments, alors que l'arbre binaire ne suit aucun ordre.
Articles Liés:
- Application de la BST
- Applications, avantages et inconvénients de l'arbre de recherche binaire
- Insertion dans l'arbre de recherche binaire (BST)
- Recherche dans l'arbre de recherche binaire (BST)
- Suppression dans l'arbre de recherche binaire (BST)
