Les limites des arbres de recherche binaires traditionnels peuvent être frustrantes. Découvrez le B-Tree, la structure de données aux multiples talents qui peut gérer facilement d'énormes quantités de données. Lorsqu'il s'agit de stocker et de rechercher de grandes quantités de données, les arbres de recherche binaires traditionnels peuvent devenir peu pratiques en raison de leurs mauvaises performances et de leur utilisation élevée de la mémoire. Les B-Trees, également connus sous le nom de B-Tree ou Balanced Tree, sont un type d’arbre auto-équilibré spécialement conçu pour surmonter ces limitations.
Contrairement aux arbres de recherche binaires traditionnels, les B-Trees se caractérisent par le grand nombre de clés qu'ils peuvent stocker dans un seul nœud, c'est pourquoi ils sont également appelés grands arbres de clés. Chaque nœud d'un B-Tree peut contenir plusieurs clés, ce qui permet à l'arbre d'avoir un facteur de branchement plus grand et donc une hauteur moins grande. Cette faible hauteur entraîne moins d'E/S disque, ce qui se traduit par des opérations de recherche et d'insertion plus rapides. Les B-Trees sont particulièrement bien adaptés aux systèmes de stockage qui ont un accès aux données lent et volumineux, tels que les disques durs, la mémoire flash et les CD-ROM.
B-Trees maintient l'équilibre en garantissant que chaque nœud dispose d'un nombre minimum de clés, de sorte que l'arborescence soit toujours équilibrée. Cet équilibre garantit que la complexité temporelle des opérations telles que l'insertion, la suppression et la recherche est toujours O (log n), quelle que soit la forme initiale de l'arborescence.
Complexité temporelle du B-Tree :
| M. Non. | Algorithme | Complexité temporelle |
|---|---|---|
| 1. | Recherche | O (log n) |
| 2. | Insérer | O (log n) |
| 3. | Supprimer | O (log n) |
Note: n est le nombre total d'éléments dans l'arbre B
java int sous forme de chaîne
Propriétés du B-Tree :
- Toutes les feuilles sont au même niveau.
- B-Tree est défini par le terme degré minimum « t ‘. La valeur de ' t ‘dépend de la taille du bloc de disque.
- Chaque nœud, à l'exception de la racine, doit contenir au moins des clés t-1. La racine peut contenir au minimum 1 clé.
- Tous les nœuds (y compris la racine) peuvent contenir au plus ( 2*t – 1 ) clés.
- Le nombre d'enfants d'un nœud est égal au nombre de clés qu'il contient plus 1 .
- Toutes les clés d'un nœud sont triées par ordre croissant. L'enfant entre deux clés k1 et k2 contient toutes les clés de la plage k1 et k2 .
- B-Tree grandit et rétrécit à partir de la racine, ce qui est différent de l'arbre de recherche binaire. Les arbres de recherche binaire grandissent vers le bas et rétrécissent également vers le bas.
- Comme d’autres arbres de recherche binaires équilibrés, la complexité temporelle de recherche, d’insertion et de suppression est O (log n).
- L'insertion d'un nœud dans B-Tree se produit uniquement au niveau du nœud feuille.
Voici un exemple de B-Tree d'ordre minimum 5
Note: que dans les B-Trees pratiques, la valeur de la commande minimale est bien supérieure à 5.

Nous pouvons voir dans le diagramme ci-dessus que tous les nœuds feuilles sont au même niveau et que tous les non-feuilles n'ont pas de sous-arbre vide et ont des clés de moins que le nombre de leurs enfants.
Faits intéressants sur les B-Trees :
- La hauteur minimale du B-Tree qui peut exister avec n nombre de nœuds et m est le nombre maximum d'enfants d'un nœud peut avoir est :
- La hauteur maximale du B-Tree qui peut exister avec n nombre de nœuds et t est le nombre minimum d'enfants qu'un nœud non racine peut avoir est :
et
Traversée dans B-Tree :
Le parcours est également similaire au parcours Inorder de l'arbre binaire. Nous commençons par l'enfant le plus à gauche, imprimons récursivement l'enfant le plus à gauche, puis répétons le même processus pour les enfants et les clés restants. En fin de compte, imprimez récursivement l’enfant le plus à droite.
Opération de recherche dans B-Tree :
La recherche est similaire à la recherche dans l’arborescence de recherche binaire. Soit la clé à rechercher est k.
- Commencez par la racine et parcourez récursivement vers le bas.
- Pour chaque nœud non-feuille visité,
- Si le nœud possède la clé, nous renvoyons simplement le nœud.
- Sinon, nous revenons à l'enfant approprié (l'enfant qui se trouve juste avant la première plus grande clé) du nœud.
- Si nous atteignons un nœud feuille et ne trouvons pas k dans le nœud feuille, alors renvoyons NULL.
La recherche d’un B-Tree est similaire à la recherche d’un arbre binaire. L'algorithme est similaire et va avec la récursion. A chaque niveau, la recherche est optimisée comme si la valeur clé n'était pas présente dans la plage du parent alors la clé est présente dans une autre branche. Comme ces valeurs limitent la recherche, elles sont également appelées valeurs limites ou valeurs de séparation. Si nous atteignons un nœud feuille et ne trouvons pas la clé souhaitée, il affichera NULL.
Algorithme de recherche d'un élément dans un B-Tree : -
C++
struct> Node {> >int> n;> >int> key[MAX_KEYS];> >Node* child[MAX_CHILDREN];> >bool> leaf;> };> Node* BtreeSearch(Node* x,>int> k) {> >int> i = 0;> >while> (i n && k>x->clé[i]) {> >i++;> >}> >if> (i n && k == x->clé[i]) {> >return> x;> >}> >if> (x->feuille) {> >return> nullptr;> >}> >return> BtreeSearch(x->enfant[i], k);> }> |
>
>
C
BtreeSearch(x, k)> >i = 1> > >// n[x] means number of keys in x node> >while> i ? n[x] and k ? keyi[x]> >do> i = i + 1> >if> i n[x] and k = keyi[x]> >then>return> (x, i)> >if> leaf [x]> >then>return> NIL> >else> >return> BtreeSearch(ci[x], k)> |
>
>
Java
class> Node {> >int> n;> >int>[] key =>new> int>[MAX_KEYS];> >Node[] child =>new> Node[MAX_CHILDREN];> >boolean> leaf;> }> Node BtreeSearch(Node x,>int> k) {> >int> i =>0>;> >while> (i = x.key[i]) {> >i++;> >}> >if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> |
>
>
Python3
class> Node:> >def> __init__(>self>):> >self>.n>=> 0> >self>.key>=> [>0>]>*> MAX_KEYS> >self>.child>=> [>None>]>*> MAX_CHILDREN> >self>.leaf>=> True> def> BtreeSearch(x, k):> >i>=> 0> >while> i and k>= x.key[i] : i += 1 si i et k == x.key[i] : return x if x.leaf : return None return BtreeSearch(x.child[i], k)> |
>
>
C#
class> Node {> >public> int> n;> >public> int>[] key =>new> int>[MAX_KEYS];> >public> Node[] child =>new> Node[MAX_CHILDREN];> >public> bool> leaf;> }> Node BtreeSearch(Node x,>int> k) {> >int> i = 0;> >while> (i = x.key[i]) {> >i++;> >}> >if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> |
>
>
Javascript
// Define a Node class with properties n, key, child, and leaf> class Node {> >constructor() {> >this>.n = 0;> >this>.key =>new> Array(MAX_KEYS);> >this>.child =>new> Array(MAX_CHILDREN);> >this>.leaf =>false>;> >}> }> // Define a function BtreeSearch that takes in a Node object x and an integer k> function> BtreeSearch(x, k) {> >let i = 0;> >while> (i = x.key[i]) {> >i++;> >}> >if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> |
>
>
Exemples:
fractionnement de chaînes c++
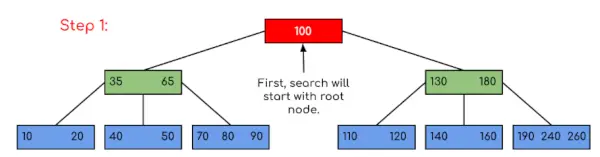
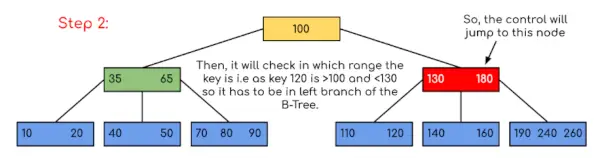
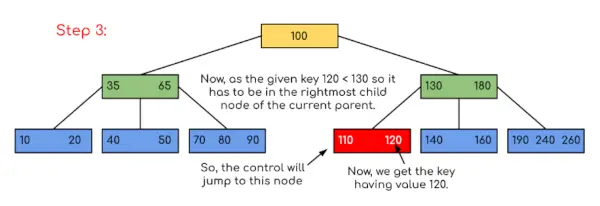
Saisir: Recherchez 120 dans le B-Tree donné.
Solution:
chaîne de garniture Java
Dans cet exemple, nous pouvons voir que notre recherche a été réduite en limitant simplement les chances que la clé contenant la valeur puisse être présente. De même, si dans l'exemple ci-dessus nous devons rechercher 180, alors le contrôle s'arrêtera à l'étape 2 car le programme constatera que la clé 180 est présente dans le nœud actuel. Et de même, s'il s'agit de rechercher 90, alors 90 <100, donc il ira automatiquement vers le sous-arbre de gauche, et donc le flux de contrôle se déroulera de la même manière que celui indiqué dans l'exemple ci-dessus.
Vous trouverez ci-dessous la mise en œuvre de l’approche ci-dessus :
C++
// C++ implementation of search() and traverse() methods> #include> using> namespace> std;> // A BTree node> class> BTreeNode {> >int>* keys;>// An array of keys> >int> t;>// Minimum degree (defines the range for number> >// of keys)> >BTreeNode** C;>// An array of child pointers> >int> n;>// Current number of keys> >bool> leaf;>// Is true when node is leaf. Otherwise false> public>:> >BTreeNode(>int> _t,>bool> _leaf);>// Constructor> >// A function to traverse all nodes in a subtree rooted> >// with this node> >void> traverse();> >// A function to search a key in the subtree rooted with> >// this node.> >BTreeNode*> >search(>int> k);>// returns NULL if k is not present.> >// Make the BTree friend of this so that we can access> >// private members of this class in BTree functions> >friend> class> BTree;> };> // A BTree> class> BTree {> >BTreeNode* root;>// Pointer to root node> >int> t;>// Minimum degree> public>:> >// Constructor (Initializes tree as empty)> >BTree(>int> _t)> >{> >root = NULL;> >t = _t;> >}> >// function to traverse the tree> >void> traverse()> >{> >if> (root != NULL)> >root->traverse();> >}> >// function to search a key in this tree> >BTreeNode* search(>int> k)> >{> >return> (root == NULL) ? NULL : root->recherche(k);> >}> };> // Constructor for BTreeNode class> BTreeNode::BTreeNode(>int> _t,>bool> _leaf)> {> >// Copy the given minimum degree and leaf property> >t = _t;> >leaf = _leaf;> >// Allocate memory for maximum number of possible keys> >// and child pointers> >keys =>new> int>[2 * t - 1];> >C =>new> BTreeNode*[2 * t];> >// Initialize the number of keys as 0> >n = 0;> }> // Function to traverse all nodes in a subtree rooted with> // this node> void> BTreeNode::traverse()> {> >// There are n keys and n+1 children, traverse through n> >// keys and first n children> >int> i;> >for> (i = 0; i // If this is not leaf, then before printing key[i], // traverse the subtree rooted with child C[i]. if (leaf == false) C[i]->traverser(); cout<< ' ' << keys[i]; } // Print the subtree rooted with last child if (leaf == false) C[i]->traverser(); } // Fonction pour rechercher la clé k dans le sous-arbre enraciné avec ce nœud BTreeNode* BTreeNode::search(int k) { // Trouver la première clé supérieure ou égale à k int i = 0; while (i touches[i]) i++; // Si la clé trouvée est égale à k, renvoie ce nœud if (keys[i] == k) return this ; // Si la clé n'est pas trouvée ici et qu'il s'agit d'un nœud feuille if (leaf == true) return NULL ; // Aller à l'enfant approprié return C[i]->search(k); }> |
>
>
Java
// Java program to illustrate the sum of two numbers> // A BTree> class> Btree {> >public> BTreeNode root;>// Pointer to root node> >public> int> t;>// Minimum degree> >// Constructor (Initializes tree as empty)> >Btree(>int> t)> >{> >this>.root =>null>;> >this>.t = t;> >}> >// function to traverse the tree> >public> void> traverse()> >{> >if> (>this>.root !=>null>)> >this>.root.traverse();> >System.out.println();> >}> >// function to search a key in this tree> >public> BTreeNode search(>int> k)> >{> >if> (>this>.root ==>null>)> >return> null>;> >else> >return> this>.root.search(k);> >}> }> // A BTree node> class> BTreeNode {> >int>[] keys;>// An array of keys> >int> t;>// Minimum degree (defines the range for number> >// of keys)> >BTreeNode[] C;>// An array of child pointers> >int> n;>// Current number of keys> >boolean> >leaf;>// Is true when node is leaf. Otherwise false> >// Constructor> >BTreeNode(>int> t,>boolean> leaf)> >{> >this>.t = t;> >this>.leaf = leaf;> >this>.keys =>new> int>[>2> * t ->1>];> >this>.C =>new> BTreeNode[>2> * t];> >this>.n =>0>;> >}> >// A function to traverse all nodes in a subtree rooted> >// with this node> >public> void> traverse()> >{> >// There are n keys and n+1 children, traverse> >// through n keys and first n children> >int> i =>0>;> >for> (i =>0>; i <>this>.n; i++) {> >// If this is not leaf, then before printing> >// key[i], traverse the subtree rooted with> >// child C[i].> >if> (>this>.leaf ==>false>) {> >C[i].traverse();> >}> >System.out.print(keys[i] +>' '>);> >}> >// Print the subtree rooted with last child> >if> (leaf ==>false>)> >C[i].traverse();> >}> >// A function to search a key in the subtree rooted with> >// this node.> >BTreeNode search(>int> k)> >{>// returns NULL if k is not present.> >// Find the first key greater than or equal to k> >int> i =>0>;> >while> (i keys[i])> >i++;> >// If the found key is equal to k, return this node> >if> (keys[i] == k)> >return> this>;> >// If the key is not found here and this is a leaf> >// node> >if> (leaf ==>true>)> >return> null>;> >// Go to the appropriate child> >return> C[i].search(k);> >}> }> |
>
>
Python3
# Create a node> class> BTreeNode:> >def> __init__(>self>, leaf>=>False>):> >self>.leaf>=> leaf> >self>.keys>=> []> >self>.child>=> []> # Tree> class> BTree:> >def> __init__(>self>, t):> >self>.root>=> BTreeNode(>True>)> >self>.t>=> t> ># Insert node> >def> insert(>self>, k):> >root>=> self>.root> >if> len>(root.keys)>=>=> (>2> *> self>.t)>-> 1>:> >temp>=> BTreeNode()> >self>.root>=> temp> >temp.child.insert(>0>, root)> >self>.split_child(temp,>0>)> >self>.insert_non_full(temp, k)> >else>:> >self>.insert_non_full(root, k)> ># Insert nonfull> >def> insert_non_full(>self>, x, k):> >i>=> len>(x.keys)>-> 1> >if> x.leaf:> >x.keys.append((>None>,>None>))> >while> i>>=> 0> and> k[>0>] 0]: x.keys[i + 1] = x.keys[i] i -= 1 x.keys[i + 1] = k else: while i>= 0 et k[0] 0] : i -= 1 i += 1 si len(x.child[i].keys) == (2 * self.t) - 1 : self.split_child(x, i) if k[0]> x.keys[i][0] : i += 1 self.insert_non_full(x.child[i], k) # Diviser l'enfant def split_child(self, x, i) : t = self .t y = x.child[i] z = BTreeNode(y.leaf) x.child.insert(i + 1, z) x.keys.insert(i, y.keys[t - 1]) z.keys = y.keys[t : (2 * t) - 1] y.keys = y.keys[0 : t - 1] sinon y.leaf : z.child = y.child[t : 2 * t] y. child = y.child[0: t - 1] # Imprimer l'arbre def print_tree(self, x, l=0): print('Level ', l, ' ', len(x.keys), end=':') pour i dans x.keys : print(i, end=' ') print() l += 1 si len(x.child)> 0 : pour i dans x.child : self.print_tree(i, l) # Clé de recherche dans l'arborescence def search_key(self, k, x=None) : si x n'est pas None : i = 0 tandis que i |
>
>
C#
// C# program to illustrate the sum of two numbers> using> System;> // A BTree> class> Btree {> >public> BTreeNode root;>// Pointer to root node> >public> int> t;>// Minimum degree> >// Constructor (Initializes tree as empty)> >Btree(>int> t)> >{> >this>.root =>null>;> >this>.t = t;> >}> >// function to traverse the tree> >public> void> traverse()> >{> >if> (>this>.root !=>null>)> >this>.root.traverse();> >Console.WriteLine();> >}> >// function to search a key in this tree> >public> BTreeNode search(>int> k)> >{> >if> (>this>.root ==>null>)> >return> null>;> >else> >return> this>.root.search(k);> >}> }> // A BTree node> class> BTreeNode {> >int>[] keys;>// An array of keys> >int> t;>// Minimum degree (defines the range for number> >// of keys)> >BTreeNode[] C;>// An array of child pointers> >int> n;>// Current number of keys> >bool> leaf;>// Is true when node is leaf. Otherwise false> >// Constructor> >BTreeNode(>int> t,>bool> leaf)> >{> >this>.t = t;> >this>.leaf = leaf;> >this>.keys =>new> int>[2 * t - 1];> >this>.C =>new> BTreeNode[2 * t];> >this>.n = 0;> >}> >// A function to traverse all nodes in a subtree rooted> >// with this node> >public> void> traverse()> >{> >// There are n keys and n+1 children, traverse> >// through n keys and first n children> >int> i = 0;> >for> (i = 0; i <>this>.n; i++) {> >// If this is not leaf, then before printing> >// key[i], traverse the subtree rooted with> >// child C[i].> >if> (>this>.leaf ==>false>) {> >C[i].traverse();> >}> >Console.Write(keys[i] +>' '>);> >}> >// Print the subtree rooted with last child> >if> (leaf ==>false>)> >C[i].traverse();> >}> >// A function to search a key in the subtree rooted with> >// this node.> >public> BTreeNode search(>int> k)> >{>// returns NULL if k is not present.> >// Find the first key greater than or equal to k> >int> i = 0;> >while> (i keys[i])> >i++;> >// If the found key is equal to k, return this node> >if> (keys[i] == k)> >return> this>;> >// If the key is not found here and this is a leaf> >// node> >if> (leaf ==>true>)> >return> null>;> >// Go to the appropriate child> >return> C[i].search(k);> >}> }> // This code is contributed by Rajput-Ji> |
>
>
Javascript
// Javascript program to illustrate the sum of two numbers> // A BTree> class Btree> {> >// Constructor (Initializes tree as empty)> >constructor(t)> >{> >this>.root =>null>;> >this>.t = t;> >}> > >// function to traverse the tree> >traverse()> >{> >if> (>this>.root !=>null>)> >this>.root.traverse();> >document.write(>' '>);> >}> > >// function to search a key in this tree> >search(k)> >{> >if> (>this>.root ==>null>)> >return> null>;> >else> >return> this>.root.search(k);> >}> > }> // A BTree node> class BTreeNode> {> >// Constructor> >constructor(t,leaf)> >{> >this>.t = t;> >this>.leaf = leaf;> >this>.keys =>new> Array(2 * t - 1);> >this>.C =>new> Array(2 * t);> >this>.n = 0;> >}> >// A function to traverse all nodes in a subtree rooted with this node> >traverse()> >{> >// There are n keys and n+1 children, traverse through n keys> >// and first n children> >let i = 0;> >for> (i = 0; i <>this>.n; i++) {> > >// If this is not leaf, then before printing key[i],> >// traverse the subtree rooted with child C[i].> >if> (>this>.leaf ==>false>) {> >C[i].traverse();> >}> >document.write(keys[i] +>' '>);> >}> > >// Print the subtree rooted with last child> >if> (leaf ==>false>)> >C[i].traverse();> >}> > >// A function to search a key in the subtree rooted with this node.> >search(k)>// returns NULL if k is not present.> >{> > >// Find the first key greater than or equal to k> >let i = 0;> >while> (i keys[i])> >i++;> > >// If the found key is equal to k, return this node> >if> (keys[i] == k)> >return> this>;> > >// If the key is not found here and this is a leaf node> >if> (leaf ==>true>)> >return> null>;> > >// Go to the appropriate child> >return> C[i].search(k);> >}> }> // This code is contributed by patel2127> |
>
>
Note: Le code ci-dessus ne contient pas le programme pilote. Nous couvrirons le programme complet dans notre prochain article sur Insertion d'un arbre B .
Il existe deux conventions pour définir un B-Tree, l'une consiste à définir par degré minimum, la seconde consiste à définir par ordre. Nous avons suivi la convention relative au diplôme minimum et suivrons la même chose dans les prochains articles sur B-Tree. Les noms de variables utilisés dans le programme ci-dessus restent également les mêmes
se connecter à une base de données java
Applications des arbres B :
- Il est utilisé dans les grandes bases de données pour accéder aux données stockées sur le disque
- La recherche de données dans un ensemble de données peut être réalisée en beaucoup moins de temps grâce au B-Tree
- Avec la fonction d'indexation, une indexation à plusieurs niveaux peut être réalisée.
- La plupart des serveurs utilisent également l'approche B-tree.
- Les B-Trees sont utilisés dans les systèmes de CAO pour organiser et rechercher des données géométriques.
- Les B-Trees sont également utilisés dans d’autres domaines tels que le traitement du langage naturel, les réseaux informatiques et la cryptographie.
Avantages des B-Trees :
- Les B-Trees ont une complexité temporelle garantie de O(log n) pour les opérations de base telles que l'insertion, la suppression et la recherche, ce qui les rend adaptés aux grands ensembles de données et aux applications en temps réel.
- Les B-Trees sont auto-équilibrés.
- Haute concurrence et haut débit.
- Utilisation efficace du stockage.
Inconvénients des B-Trees :
- Les B-Trees sont basés sur des structures de données basées sur disque et peuvent avoir une utilisation élevée du disque.
- Pas le meilleur dans tous les cas.
- Lent par rapport à d’autres structures de données.
Insertion et suppression :
Insertion d'un arbre B
Suppression de l'arbre B