Le monde algorithmique est magnifique avec de multiples stratégies et outils développés 24 heures sur 24 pour répondre aux besoins du calcul haute performance. En effet, lorsque les algorithmes s’inspirent des lois naturelles, des résultats intéressants sont observés. Les algorithmes évolutionnaires appartiennent à une telle classe d’algorithmes. Ces algorithmes sont conçus de manière à imiter certains comportements ainsi que des traits évolutifs du génome humain. De plus, une telle conception algorithmique n’est pas seulement limitée aux humains mais peut également s’inspirer du comportement naturel de certains animaux. L’objectif fondamental de la fabrication de telles méthodologies est de fournir des solutions réalistes, pertinentes et néanmoins peu coûteuses à des problèmes jusqu’à présent insolubles par les moyens conventionnels.

Différentes techniques d'optimisation ont ainsi évolué sur la base de ces algorithmes évolutifs et ont ainsi ouvert le domaine des métaheuristiques. Métaheuristique est dérivé de deux mots grecs, à savoir, Méta signification un niveau au dessus et heuriskein signification trouver . Des algorithmes tels que l'optimisation des essaims de particules (PSO) et l'optimisation des colonies de fourmis (ACO) sont des exemples d'intelligence en essaim et de métaheuristiques. L’objectif de l’intelligence en essaim est de concevoir des systèmes multi-agents intelligents en s’inspirant du comportement collectif des insectes sociaux tels que les fourmis, les termites, les abeilles, les guêpes et d’autres sociétés animales telles que les troupeaux d’oiseaux ou les bancs de poissons.

Arrière-plan:

La technique d'optimisation des colonies de fourmis est purement inspirée du recherche de nourriture comportement des colonies de fourmis, introduit pour la première fois par Marco Dorigo dans les années 1990. Les fourmis sont des insectes eusociaux qui préfèrent la survie et le maintien de la communauté plutôt que leur espèce individuelle. Ils communiquent entre eux par le son, le toucher et les phéromones. Phéromones sont des composés chimiques organiques sécrétés par les fourmis qui déclenchent une réponse sociale chez les membres de la même espèce. Ce sont des produits chimiques capables d’agir comme des hormones en dehors du corps de l’individu sécréteur, pour avoir un impact sur le comportement des individus récepteurs. Puisque la plupart des fourmis vivent au sol, elles utilisent la surface du sol pour laisser des traces de phéromones qui peuvent être suivies (odorées) par d’autres fourmis.
Les fourmis vivent dans des nids communautaires et le principe sous-jacent de l'ACO est d'observer le mouvement des fourmis hors de leurs nids afin de rechercher de la nourriture sur le chemin le plus court possible. Au début, les fourmis commencent à se déplacer de manière aléatoire à la recherche de nourriture autour de leur nid. Cette recherche aléatoire ouvre plusieurs itinéraires depuis le nid jusqu'à la source de nourriture. Désormais, en fonction de la qualité et de la quantité de la nourriture, les fourmis ramènent une partie de la nourriture avec la concentration de phéromones nécessaire sur son chemin de retour. En fonction de ces essais de phéromones, la probabilité de sélection d'un chemin spécifique par les fourmis suivantes serait un facteur déterminant pour la source de nourriture. Évidemment, cette probabilité repose sur la concentration ainsi que sur le taux d’évaporation de la phéromone. On peut également observer que puisque le taux d’évaporation de la phéromone est également un facteur décisif, la longueur de chaque trajet peut facilement être prise en compte.

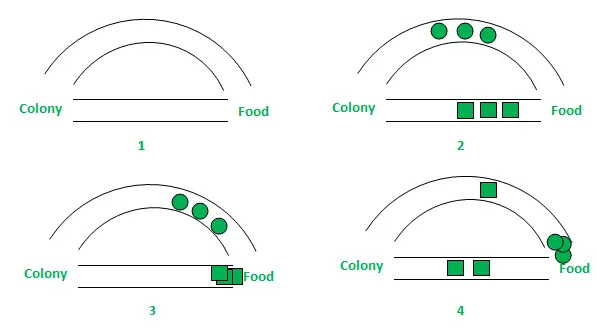
Dans la figure ci-dessus, par souci de simplicité, seuls deux chemins possibles ont été considérés entre la source de nourriture et le nid de fourmis. Les étapes peuvent être analysées comme suit :

Étape 1 : Toutes les fourmis sont dans leur nid. Il n'y a aucune teneur en phéromones dans l'environnement. (Pour la conception algorithmique, la quantité résiduelle de phéromones peut être prise en compte sans interférer avec la probabilité) Étape 2 : Les fourmis commencent leur recherche avec une probabilité égale (0,5 chacune) le long de chaque chemin. De toute évidence, le chemin courbe est le plus long et donc le temps mis par les fourmis pour atteindre la source de nourriture est plus long que l'autre. Étape 3 : Les fourmis empruntant le chemin le plus court atteignent la source de nourriture plus tôt. Maintenant, ils sont évidemment confrontés à un dilemme de sélection similaire, mais cette fois, en raison de la traînée de phéromones le long du chemin plus court déjà disponible, la probabilité de sélection est plus élevée. Étape 4 : davantage de fourmis reviennent par le chemin le plus court et les concentrations de phéromones augmentent également. De plus, en raison de l’évaporation, la concentration de phéromones dans le trajet le plus long diminue, ce qui diminue la probabilité de sélection de ce trajet dans les étapes ultérieures. Par conséquent, toute la colonie utilise progressivement le chemin le plus court avec des probabilités plus élevées. Ainsi, l’optimisation du chemin est atteinte.

Conception algorithmique :

Concernant le comportement des fourmis ci-dessus, une conception algorithmique peut maintenant être développée. Par souci de simplicité, une seule source de nourriture et une seule colonie de fourmis ont été considérées avec seulement deux voies de traversée possibles. L'ensemble du scénario peut être réalisé grâce à des graphiques pondérés où la colonie de fourmis et la source de nourriture agissent comme des sommets (ou nœuds) ; les chemins servent de bords et les valeurs de phéromones sont les poids associés aux bords.
Soit le graphique G = (V,E) où V, E sont les arêtes et les sommets du graphe. Les sommets selon notre considération sont DANS_s (Sommet source – colonie de fourmis) et DANS_d (Sommet de destination – Source de nourriture), Les deux arêtes sont ET₁ et ET₂ avec des longueurs L₁ et L₂ attribué à chacun. Maintenant, les valeurs de phéromones associées (indicatrices de leur force) peuvent être supposées être R.₁ et R.₂ pour les sommets E₁et E₂respectivement. Ainsi pour chaque fourmi, la probabilité de départ de sélection de chemin (entre E₁et E₂) peut s’exprimer ainsi :

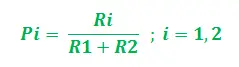
Évidemment, si R₁>R₂, la probabilité de choisir E₁est plus élevé et vice versa. Maintenant, en revenant par ce chemin le plus court, dites E_je, la valeur de la phéromone est mise à jour pour le chemin correspondant. La mise à jour se fait en fonction de la longueur des trajets ainsi que du taux d'évaporation des phéromones. Ainsi, la mise à jour peut être réalisée par étapes comme suit :

En fonction de la longueur du trajet –

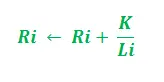
Dans la mise à jour ci-dessus, i = 1, 2 et « K » sert de paramètre du modèle. De plus, la mise à jour dépend de la longueur du chemin. Plus le chemin est court, plus la phéromone ajoutée est élevée. Conformément au taux d’évaporation de la phéromone –

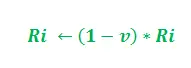
Le paramètre «v» appartient à l'intervalle (0, 1] qui régule l'évaporation des phéromones. De plus, i = 1, 2.

A chaque itération, toutes les fourmis sont placées au sommet source V_s(colonie de fourmis). Par la suite, les fourmis se déplacent de V_sà V_d(source de nourriture) après l'étape 1. Ensuite, toutes les fourmis effectuent leur voyage de retour et renforcent le chemin qu'elles ont choisi en fonction de l'étape 2.

Pseudocode :

 Procedure AntColonyOptimization: Initialize necessary parameters and pheromone trials; while not termination do : Generate ant population; Calculate fitness values associated with each ant; Find best solution through selection methods; Update pheromone trial; end while end procedure>

La mise à jour des phéromones et les calculs de fitness dans le pseudocode ci-dessus peuvent être trouvés grâce aux implémentations étape par étape mentionnées ci-dessus.
Ainsi, l’introduction de la technique d’optimisation ACO a été établie. L'application de l'ACO peut être étendue à diverses problématiques comme la fameuse TSP (problème du voyageur de commerce) .

Les références:
https://www.ics.uci.edu/~welling/teaching/271fall09/antcolonyopt.pdf