• L'algorithme d'escalade est un algorithme de recherche locale qui se déplace continuellement dans le sens d'une élévation/valeur croissante pour trouver le sommet de la montagne ou la meilleure solution au problème. Il se termine lorsqu'il atteint une valeur maximale où aucun voisin n'a une valeur supérieure.
• L'algorithme d'escalade est une technique utilisée pour optimiser les problèmes mathématiques. L'un des exemples largement discutés d'algorithme d'escalade est le problème du voyageur de commerce dans lequel nous devons minimiser la distance parcourue par le vendeur.
• On l'appelle également recherche locale gourmande car elle ne s'intéresse qu'à son bon voisin immédiat et pas au-delà.
• Un nœud d'algorithme d'escalade de colline comporte deux composants qui sont l'état et la valeur.
• Hill Climbing est principalement utilisé lorsqu’une bonne heuristique est disponible.
• Dans cet algorithme, nous n'avons pas besoin de maintenir et de gérer l'arbre ou le graphique de recherche car il ne conserve qu'un seul état actuel.

Caractéristiques de l'escalade :

Voici quelques caractéristiques principales de l’algorithme d’escalade :

Générer et tester une variante :Hill Climbing est la variante de la méthode Generate and Test. Les méthodes Générer et Test produisent des commentaires qui aident à décider dans quelle direction se déplacer dans l'espace de recherche.Approche gourmande :La recherche par algorithme d'escalade évolue dans la direction qui optimise le coût.Pas de retour en arrière :Il ne revient pas en arrière dans l’espace de recherche, car il ne se souvient pas des états précédents.

Diagramme d'espace d'état pour l'escalade :

Le paysage de l'espace d'états est une représentation graphique de l'algorithme d'escalade qui montre un graphique entre les différents états de l'algorithme et la fonction objectif/coût.

Sur l'axe Y, nous avons pris la fonction qui peut être une fonction objectif ou une fonction de coût, et l'espace d'état sur l'axe X. Si la fonction sur l'axe Y est le coût, le but de la recherche est de trouver le minimum global et le minimum local. Si la fonction de l'axe Y est une fonction objectif, alors le but de la recherche est de trouver le maximum global et le maximum local.

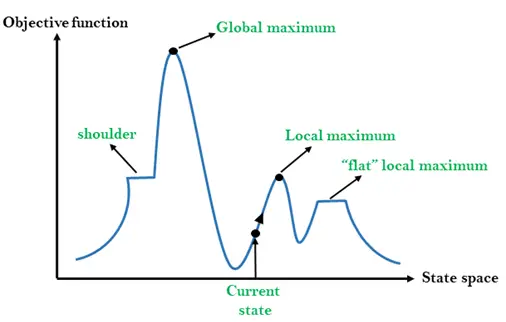
Différentes régions du paysage spatial d’État :

Maximum local : Le maximum local est un état qui est meilleur que ses états voisins, mais il existe aussi un autre état qui est supérieur à lui.

cadre de collecte Java

Maximum global : Le maximum global est le meilleur état possible du paysage spatial d’état. Il a la plus haute valeur de fonction objective.

État actuel : Il s'agit d'un état dans un diagramme de paysage où un agent est actuellement présent.

Maximum local forfaitaire : C'est un espace plat dans le paysage où tous les états voisins des états actuels ont la même valeur.

Épaule: C'est une région de plateau qui présente une pente ascendante.

système d'exploitation Linux

Types d’algorithmes d’escalade :

• Escalade simple :
• Escalade la plus raide :
• Escalade stochastique :

1. Escalade simple :

L'escalade simple est le moyen le plus simple d'implémenter un algorithme d'escalade. Il évalue uniquement l'état du nœud voisin à la fois et sélectionne le premier qui optimise le coût actuel et le définit comme état actuel. . Il vérifie uniquement qu'il s'agit d'un état successeur, et s'il trouve meilleur que l'état actuel, alors déplacez-vous sinon dans le même état. Cet algorithme présente les fonctionnalités suivantes :

• Moins de temps
• Solution moins optimale et la solution n’est pas garantie

Algorithme pour l'escalade simple :

Étape 1:Évaluez l'état initial, s'il s'agit de l'état objectif, puis renvoyez le succès et l'arrêt.Étape 2:Boucle jusqu'à ce qu'une solution soit trouvée ou qu'il ne reste plus de nouvel opérateur à postuler.Étape 3:Sélectionnez et appliquez un opérateur à l’état actuel.Étape 4:Vérifiez le nouvel état :
1. S'il s'agit d'un état d'objectif, renvoyez le succès et quittez.
2. Sinon, s'il est meilleur que l'état actuel, attribuez un nouvel état comme état actuel.
3. Sinon, si ce n’est pas meilleur que l’état actuel, revenez à l’étape 2.
Étape 5 :Sortie.

2. Escalade la plus raide :

L’algorithme de montée la plus raide est une variante de l’algorithme simple d’escalade. Cet algorithme examine tous les nœuds voisins de l'état actuel et sélectionne un nœud voisin le plus proche de l'état objectif. Cet algorithme consomme plus de temps car il recherche plusieurs voisins

Algorithme pour l'escalade des pentes les plus raides :

Étape 1:Évaluez l'état initial, s'il s'agit de l'état objectif, puis renvoyez le succès et arrêtez, sinon faites de l'état actuel l'état initial.Étape 2:Bouclez jusqu'à ce qu'une solution soit trouvée ou que l'état actuel ne change pas.
1. Laissez le SUCC être un État tel que tout successeur de l’État actuel sera meilleur que lui.
2. Pour chaque opérateur qui s'applique à l'état actuel :
   1. Appliquez le nouvel opérateur et générez un nouvel état.
   2. Évaluez le nouvel état.
   3. S'il s'agit d'un état objectif, renvoyez-le et quittez-le, sinon comparez-le au SUCC.
   4. Si c'est mieux que SUCC, définissez le nouvel état sur SUCC.
   5. Si le SUCC est meilleur que l’état actuel, définissez l’état actuel sur SUCC.
Étape 5 :Sortie.

3. Escalade stochastique :

L'escalade stochastique n'examine pas tout son voisin avant de se déplacer. Au lieu de cela, cet algorithme de recherche sélectionne un nœud voisin au hasard et décide s'il doit le choisir comme état actuel ou examiner un autre état.

Problèmes liés à l'algorithme d'escalade :

1. Maximum local : Un maximum local est un état de pointe dans le paysage qui est meilleur que chacun de ses états voisins, mais il existe également un autre état présent qui est supérieur au maximum local.

Solution: La technique de retour en arrière peut être une solution au maximum local dans le paysage spatial d’états. Créez une liste des chemins prometteurs afin que l'algorithme puisse revenir en arrière dans l'espace de recherche et explorer également d'autres chemins.

2. Plateaux : Un plateau est la zone plate de l'espace de recherche dans laquelle tous les états voisins de l'état actuel contiennent la même valeur, car cet algorithme ne trouve pas de meilleure direction pour se déplacer. Une recherche d'escalade pourrait être perdue dans la zone du plateau.

Solution: La solution pour le plateau est de faire de grands pas ou de très petits pas pendant la recherche, pour résoudre le problème. Sélectionnez au hasard un état éloigné de l'état actuel afin qu'il soit possible que l'algorithme puisse trouver une région hors plateau.

fonctions de chaîne Java

3. Crêtes : Une crête est une forme particulière du maximum local. Il a une superficie plus élevée que ses environs, mais il présente lui-même une pente et ne peut être atteint d'un seul mouvement.

Solution: En utilisant la recherche bidirectionnelle ou en nous déplaçant dans des directions différentes, nous pouvons améliorer ce problème.

Recuit simulé :

Un algorithme de montée en pente qui n'avance jamais vers une valeur inférieure garantie incomplète car pouvant rester bloqué sur un maximum local. Et si l'algorithme applique une marche aléatoire, en déplaçant un successeur, alors il peut se terminer mais pas être efficace. Recuit simulé est un algorithme qui offre à la fois efficacité et exhaustivité.

En terme mécanique Recuit est un processus de durcissement d'un métal ou d'un verre à une température élevée, puis de refroidissement progressif, ce qui permet au métal d'atteindre un état cristallin à faible énergie. Le même processus est utilisé dans le recuit simulé dans lequel l'algorithme sélectionne un mouvement aléatoire, au lieu de choisir le meilleur mouvement. Si le mouvement aléatoire améliore l’état, alors il suit le même chemin. Sinon, l’algorithme suit le chemin qui a une probabilité inférieure à 1 ou il descend et choisit un autre chemin.