Dans cette section, nous discuterons de la méthode de conversion de NFA en son équivalent DFA. Dans NFA, lorsqu'une entrée spécifique est donnée à l'état actuel, la machine passe à plusieurs états. Il peut y avoir zéro, un ou plusieurs mouvements sur un symbole d'entrée donné. En revanche, dans DFA, lorsqu'une entrée spécifique est donnée à l'état actuel, la machine ne passe qu'à un seul état. DFA ne dispose que d'un seul mouvement sur un symbole d'entrée donné.
Soit M = (Q, ∑, δ, q0, F) est un NFA qui accepte le langage L(M). Il devrait y avoir un DFA équivalent noté M' = (Q', ∑', q0', δ', F') tel que L(M) = L(M').
Étapes de conversion de NFA en DFA :
Étape 1: Initialement Q' = ϕ
Étape 2: Ajoutez q0 de NFA à Q'. Trouvez ensuite les transitions à partir de cet état de départ.
Étape 3: Dans Q', trouvez l'ensemble d'états possible pour chaque symbole d'entrée. Si cet ensemble d'états n'est pas dans Q', alors ajoutez-le à Q'.
Étape 4: Dans DFA, l'état final sera tous les états qui contiennent F (états finaux de NFA)
Exemple 1:
Convertissez le NFA donné en DFA.
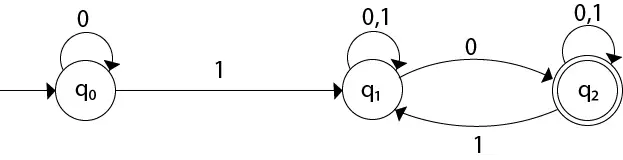
Solution: Pour le diagramme de transition donné, nous allons d’abord construire la table de transition.
| État | 0 | 1 |
|---|---|---|
| →q0 | q0 | q1 |
| q1 | {q1, q2} | q1 |
| *q2 | q2 | {q1, q2} |
Nous allons maintenant obtenir la transition δ' pour l'état q0.
δ'([q0], 0) = [q0] δ'([q0], 1) = [q1]
La transition δ' pour l'état q1 est obtenue comme :
ipconfig sur Ubuntu
δ'([q1], 0) = [q1, q2] (new state generated) δ'([q1], 1) = [q1]
La transition δ' pour l'état q2 est obtenue comme :
δ'([q2], 0) = [q2] δ'([q2], 1) = [q1, q2]
Nous allons maintenant obtenir la transition δ' sur [q1, q2].
δ'([q1, q2], 0) = δ(q1, 0) ∪ δ(q2, 0) = {q1, q2} ∪ {q2} = [q1, q2] δ'([q1, q2], 1) = δ(q1, 1) ∪ δ(q2, 1) = {q1} ∪ {q1, q2} = {q1, q2} = [q1, q2] L'état [q1, q2] est également l'état final car il contient un état final q2. La table de transition pour le DFA construit sera :
| État | 0 | 1 |
|---|---|---|
| →[q0] | [q0] | [q1] |
| [q1] | [q1, q2] | [q1] |
| *[q2] | [q2] | [q1, q2] |
| *[q1, q2] | [q1, q2] | [q1, q2] |
Le diagramme de transition sera :

L’état q2 peut être éliminé car q2 est un état inaccessible.
Exemple 2 :
Convertissez le NFA donné en DFA.

Solution: Pour le diagramme de transition donné, nous allons d’abord construire la table de transition.
| État | 0 | 1 |
|---|---|---|
| →q0 | {q0, q1} | {q1} |
| *q1 | ϕ | {q0, q1} |
Nous allons maintenant obtenir la transition δ' pour l'état q0.
δ'([q0], 0) = {q0, q1} = [q0, q1] (new state generated) δ'([q0], 1) = {q1} = [q1] La transition δ' pour l'état q1 est obtenue comme :
δ'([q1], 0) = ϕ δ'([q1], 1) = [q0, q1]
Nous allons maintenant obtenir la transition δ' sur [q0, q1].
δ'([q0, q1], 0) = δ(q0, 0) ∪ δ(q1, 0) = {q0, q1} ∪ ϕ = {q0, q1} = [q0, q1] De la même manière,
base de données sur les propriétés des acides
δ'([q0, q1], 1) = δ(q0, 1) ∪ δ(q1, 1) = {q1} ∪ {q0, q1} = {q0, q1} = [q0, q1] Comme dans le NFA donné, q1 est un état final, puis dans DFA, partout où q1 existe, cet état devient un état final. Par conséquent, dans le DFA, les états finaux sont [q1] et [q0, q1]. Donc ensemble d'états finaux F = {[q1], [q0, q1]}.
La table de transition pour le DFA construit sera :
| État | 0 | 1 |
|---|---|---|
| →[q0] | [q0, q1] | [q1] |
| *[q1] | ϕ | [q0, q1] |
| *[q0, q1] | [q0, q1] | [q0, q1] |
Le diagramme de transition sera :

Même nous pouvons changer le nom des États du DFA.
Supposer
A = [q0] B = [q1] C = [q0, q1]
Avec ces nouveaux noms le DFA sera le suivant :

