La méthode gourmande est l’une des stratégies comme Diviser pour régner utilisée pour résoudre les problèmes. Cette méthode est utilisée pour résoudre des problèmes d’optimisation. Un problème d'optimisation est un problème qui exige des résultats maximaux ou minimaux. Comprenons à travers quelques termes.
La méthode Greedy est l’approche la plus simple et la plus directe. Ce n'est pas un algorithme, mais c'est une technique. La fonction principale de cette approche est que la décision est prise sur la base des informations actuellement disponibles. Quelles que soient les informations actuelles, la décision est prise sans se soucier de l'effet de la décision actuelle dans le futur.
maître d'origine git pull
Cette technique est essentiellement utilisée pour déterminer la solution réalisable qui peut être optimale ou non. La solution réalisable est un sous-ensemble qui satisfait aux critères donnés. La solution optimale est la solution qui est la meilleure et la plus favorable du sous-ensemble. Dans le cas du réalisable, si plusieurs solutions satisfont aux critères donnés, alors ces solutions seront considérées comme réalisables, alors que la solution optimale est la meilleure solution parmi toutes les solutions.
Caractéristiques de la méthode Greedy
Voici les caractéristiques d’une méthode gloutonne :
- Pour construire la solution de manière optimale, cet algorithme crée deux ensembles où un ensemble contient tous les éléments choisis et un autre ensemble contient les éléments rejetés.
- Un algorithme Greedy fait de bons choix locaux dans l’espoir que la solution soit réalisable ou optimale.
Composants de l'algorithme gourmand
Les composants pouvant être utilisés dans l’algorithme glouton sont :
liste doublement chaînée
Applications de l'algorithme gourmand
- Il est utilisé pour trouver le chemin le plus court.
- Il est utilisé pour trouver l'arbre couvrant minimum en utilisant l'algorithme de prim ou l'algorithme de Kruskal.
- Il est utilisé dans un séquencement de travaux avec un délai.
- Cet algorithme est également utilisé pour résoudre le problème du sac à dos fractionnaire.
Pseudo code de l'algorithme gourmand
Algorithm Greedy (a, n) { Solution : = 0; for i = 0 to n do { x: = select(a); if feasible(solution, x) { Solution: = union(solution , x) } return solution; } } Ce qui précède est l’algorithme glouton. Initialement, la solution reçoit une valeur nulle. Nous transmettons le tableau et le nombre d'éléments dans l'algorithme glouton. Dans la boucle for, nous sélectionnons les éléments un par un et vérifions si la solution est réalisable ou non. Si la solution est réalisable, alors nous effectuons l'union.
Comprenons à travers un exemple.
Supposons qu'il y ait un problème « P ». Je souhaite voyager de A à B comme indiqué ci-dessous :
P : A → B
Le problème est que nous devons parcourir ce voyage de A à B. Il existe différentes solutions pour aller de A à B. On peut aller de A à B en marche, voiture, vélo, train, avion , etc. Il y a une contrainte dans le voyage selon laquelle nous devons effectuer ce voyage dans les 12 heures. Si je prends le train ou l'avion seulement, je peux parcourir cette distance en 12 heures. Il existe de nombreuses solutions à ce problème mais seules deux solutions satisfont à la contrainte.
Si nous disons que nous devons couvrir le voyage au coût minimum. Cela signifie que nous devons parcourir cette distance le moins possible, ce problème est donc connu sous le nom de problème de minimisation. Jusqu'à présent, nous avons deux solutions possibles, à savoir une par train et une autre par avion. Puisque voyager en train entraînera un coût minimum, c'est donc une solution optimale. Une solution optimale est également la solution réalisable, mais fournissant le meilleur résultat, de sorte que cette solution soit la solution optimale avec le coût minimum. Il n'y aurait qu'une seule solution optimale.
Le problème qui nécessite un résultat minimum ou maximum est alors connu sous le nom de problème d'optimisation. La méthode gourmande est l’une des stratégies utilisées pour résoudre les problèmes d’optimisation.
types de boucle for
Inconvénients de l’utilisation de l’algorithme Greedy
L'algorithme gourmand prend des décisions basées sur les informations disponibles à chaque phase sans tenir compte du problème plus large. Il est donc possible que la solution gourmande ne fournisse pas la meilleure solution à chaque problème.
Il suit le choix de l'optimum local à chaque étape dans le but de trouver l'optimum global. Comprenons à travers un exemple.
Considérons le graphique ci-dessous :
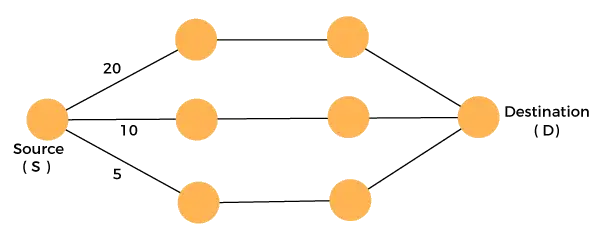
Nous devons voyager de la source à la destination au moindre coût. Puisque nous avons trois solutions réalisables ayant des chemins de coûts de 10, 20 et 5, 5 est le chemin de coût minimum, c'est donc la solution optimale. C'est l'optimum local, et de cette façon, on trouve l'optimum local à chaque étape afin de calculer la solution optimale globale.
Java statique
