Les problèmes de régression et de classification probabiliste peuvent être résolus à l'aide du processus gaussien (GP), une technique d'apprentissage supervisé. Puisque chaque processus gaussien peut être considéré comme une généralisation de dimension infinie de variables multivariées. Distributions gaussiennes , le terme gaussien apparaît dans le nom. Nous discuterons des processus de régression gaussiens dans cet article, également appelés régression de processus gaussien (GPR). De nombreux problèmes concrets dans les domaines de la science des matériaux, de la chimie, de la physique et de la biologie ont été résolus grâce à l'utilisation du GPR.
Table des matières
- Régression du processus gaussien (GPR)
- Concepts clés de la régression du processus gaussien (GPR)
- Concept mathématique de régression de processus gaussien (GPR)
- Implémentation du processus gaussien en Python
Régression du processus gaussien (GPR)
La régression par processus gaussien (GPR) est une technique de régression non paramétrique puissante et flexible utilisée dans apprentissage automatique et statistiques . Ceci est particulièrement utile lorsqu'il s'agit de problèmes impliquant des données continues, où la relation entre les variables d'entrée et la sortie n'est pas explicitement connue ou peut être complexe. Le GPR est une approche bayésienne capable de modéliser la certitude des prédictions, ce qui en fait un outil précieux pour diverses applications, notamment l'optimisation, la prévision de séries chronologiques, etc. Le GPR est basé sur le concept de processus gaussien, qui est un ensemble de variables aléatoires dont un nombre fini a une distribution gaussienne commune. Un processus gaussien peut être considéré comme une distribution de fonctions.
Concepts clés de la régression du processus gaussien (GPR)
Processus Gaussain
Un modèle probabiliste non paramétrique appelé Processus gaussien (GP) est utilisé dans les statistiques et l'apprentissage automatique pour la régression, la classification et la quantification de l'incertitude. Il représente un groupe de variables aléatoires, dont chacune a une distribution gaussienne conjointe et peut avoir un nombre fini. Les généralistes constituent une technique polyvalente et efficace pour modéliser des relations complexes dans les données et produire des prévisions avec l’incertitude associée.
Caractéristiques des processus gaussiens :
- Nature non paramétrique : Les médecins généralistes peuvent s'adapter à la complexité des données car ils ne s'appuient pas sur un nombre défini de paramètres du modèle
- Prédictions probabilistes : Les prédictions des médecins généralistes peuvent être quantifiées car elles fournissent des prédictions sous forme de distributions de probabilité.
- Interpolation et lissage : Les GP sont utiles pour les données bruitées ou échantillonnées de manière irrégulière, car ils sont efficaces pour lisser les données bruitées et interpoler entre les points de données.
- Marginalisation des hyperparamètres : En éliminant la nécessité d'un ajustement explicite des hyperparamètres, ils marginalisent les hyperparamètres, ce qui simplifie le modèle.
Fonction moyenne
La valeur prédite de la fonction modélisée à chaque point d'entrée est représentée par le fonction moyenne dans les processus gaussiens (GP). Cela fonctionne comme une présomption fondamentale concernant la structure des données sous-jacente. La fonction moyenne est fréquemment définie sur zéro par défaut, pas nécessairement et peut être modifiée en fonction des propriétés des données ou de l'expertise du domaine. En influençant la tendance centrale des prévisions, il aide les médecins généralistes à identifier des modèles ou des tendances dans les données. Les médecins généralistes fournissent des prédictions probabilistes contenant de l'incertitude ainsi que des estimations ponctuelles en incluant la fonction moyenne.
Fonction de covariance (noyau)
Le fonction de covariance , également appelée fonction noyau, mesure la similitude des points de données d'entrée les uns par rapport aux autres dans les processus gaussiens (GP). Il est essentiel pour caractériser le comportement du modèle GP, affectant la sélection des fonctions de la distribution précédente. La fonction de covariance mesure les similitudes par paires pour vérifier la corrélation entre les valeurs de la fonction. Les médecins généralistes peuvent s’adapter à un large éventail de modèles de données, depuis les tendances fluides jusqu’aux structures complexes, car différentes fonctions du noyau capturent différents types de corrélations. Les performances du modèle peuvent être grandement affectées par la sélection du noyau.
Distributions antérieures
Le distribution préalable , dans les processus gaussiens (GP), est notre compréhension des fonctions avant l'observation de toute donnée. Habituellement, il est décrit par une fonction de covariance (noyau) et une fonction de moyenne. Alors que la fonction de covariance décrit la similarité ou la corrélation entre les valeurs de fonction à différents points d'entrée, la fonction de moyenne code nos attentes précédentes. Ceci est utilisé au préalable par les médecins généralistes pour créer une répartition sur les fonctions. Dans les médecins généralistes, les priorités peuvent être sélectionnées pour représenter l'incertitude des données, intégrer la connaissance du domaine ou indiquer la fluidité.
Distributions postérieures
Processus gaussiens distribution ultérieure montre nos hypothèses révisées sur les fonctions suite à l’observation des données. Il rassemble la probabilité des données compte tenu de la fonction et de la distribution précédente. La régression postérieure de GP offre une distribution sur les fonctions qui correspondent le plus aux données observées. En permettant des prédictions probabilistes et la quantification de l'incertitude, la distribution a posteriori reflète le compromis entre les croyances a priori stockées dans la distribution a priori et les informations fournies par les données.
Concept mathématique de régression de processus gaussien (GPR)
Pour les tâches de régression, un modèle d'apprentissage automatique probabiliste non paramétrique appelé régression du processus gaussien (GP) est utilisé. Lors de la modélisation d'interactions complexes et ambiguës entre les variables d'entrée et de sortie, il s'agit d'un outil puissant. Une distribution gaussienne multivariée est supposée produire les points de données dans la régression GP, et l'objectif est de déduire cette distribution.
Le modèle de régression GP a l'expression mathématique suivante. Supposons que x1, X2,…..,Xnsont les points de données d'entrée, où x appartiennent à des nombres réels (-2,-1,0,1…), (xje
Supposons que oui1, et2 ,……., etnsont les valeurs de sortie, où yjeappartient au nombre réel (yje
Le modèle de régression GP fait l'hypothèse qu'un processus gaussien avec une fonction moyenne (
Alors, sur un ensemble d’emplacements de test x*, la distribution de f est donnée par :
Généralement, les fonctions de noyau sont utilisées pour définir la fonction moyenne et la fonction de covariance. À titre d’illustration, le noyau exponentiel carré fréquemment utilisé est décrit comme suit :
Où,
k(x_{i}, x_{j}) = La fonction noyau est représentée par ceci et calcule la corrélation ou la similarité entre deux points de données d'entrée, xjeet xj.sigma^2 = Le paramètre de variance du noyau est le suivant. Il établit l’échelle ou la répartition verticale de la fonction noyau. Il régule la mesure dans laquelle les points de données sont corrélés. Un plus hautsigma^2 donne une fonction noyau avec une plus grande variance.- exp : La fonction exponentielle est chargée d’élever e à la puissance de l’argument.
||x_{i} – x_{j}||^2 : La différence entre les points de données d'entrée, xjeet xj, est la distance euclidienne au carré. La séparation géométrique entre les points dans l'espace caractéristique est mesurée.- je2: Il s’agit d’une représentation de l’échelle de longueur ou de la longueur caractéristique du noyau. Il régule la vitesse à laquelle la fonction du noyau se détériore à mesure que les points de données sont plus éloignés les uns des autres. Un l inférieur entraîne une dégradation plus rapide du noyau.
Le modèle de régression GP applique l'inférence bayésienne pour déterminer la distribution de f qui est la plus susceptible d'avoir produit les données étant donné un ensemble de données d'entraînement (x, y). Pour ce faire, il faut calculer la distribution a posteriori de f étant donné les données, qui est définie comme suit :
où la probabilité marginale des données est p(y|x), la distribution a priori de f est p(f) et la vraisemblance des données étant donné la fonction f est (y|x,f).
types de référence Java
Après avoir appris la distribution a posteriori de f, le modèle calcule la distribution prédictive a posteriori pour faire des prédictions sur des points de test supplémentaires x*. Il peut être défini comme suit :
Où,
p(f^*|x*, y, x) = Ceci montre, étant donné les données d'entraînement y et x, la probabilité conditionnelle des valeurs de fonction prédites f*à un nouveau point d'entrée x*En d’autres termes, il s’agit de la distribution de probabilité sur toutes les valeurs de fonction potentielles sur le nouveau site d’entrée x*, conditionné par les données observées y et leurs emplacements d'entrée correspondants x.int p(f^*|x^*, f)p(f|y,x)df = Une intégrale est utilisée dans cette section de l'équation pour déterminer la probabilité conditionnelle. L'intégrale englobe toutes les valeurs potentielles de la fonction f.p(f^*|x^*, f) = Il s'agit de la distribution de probabilité conditionnelle des valeurs de fonction attendues f*à x*, étant donné les valeurs de fonction f à certains emplacements intermédiaires.p(f|y,x) = Étant donné les données observées (y) et leurs emplacements d'entrée (x), il s'agit de la distribution de probabilité conditionnelle des valeurs de fonction (f).
Pour des tâches telles que la prise de décision tenant compte de l’incertitude et l’apprentissage actif, cette distribution offre une mesure de l’incertitude de la prédiction, ce qui peut être utile.
Étapes de la régression du processus gaussien
- Collecte de données : Rassemblez les paires de données entrée-sortie pour votre problème de régression.
- Choisissez une fonction du noyau : Sélectionnez une fonction de covariance (noyau) appropriée qui convient à votre problème. Le choix du noyau influence la forme des fonctions que GPR peut modéliser.
- Optimisation des paramètres : Estimez les hyperparamètres de la fonction noyau en maximisant la vraisemblance des données. Cela peut être fait en utilisant des techniques d'optimisation telles que la descente de gradient.
- Prédiction: Étant donné une nouvelle entrée, utilisez le modèle GPR entraîné pour faire des prédictions. GPR fournit à la fois la moyenne prévue et l’incertitude (variance) associée.
Implémentation de la régression du processus gaussien (GPR)
Python import numpy as np import matplotlib.pyplot as plt from sklearn.gaussian_process import GaussianProcessRegressor from sklearn.gaussian_process.kernels import RBF from sklearn.model_selection import train_test_split # Generate sample data np.random.seed(0) X = np.sort(5 * np.random.rand(80, 1), axis=0) y = np.sin(X).ravel() # Add noise to the data y += 0.1 * np.random.randn(80) # Define the kernel (RBF kernel) kernel = 1.0 * RBF(length_scale=1.0) # Create a Gaussian Process Regressor with the defined kernel gp = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=10) # Split the data into training and testing sets X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.5, random_state=0) # Fit the Gaussian Process model to the training data gp.fit(X_train, y_train) # Make predictions on the test data y_pred, sigma = gp.predict(X_test, return_std=True) # Visualize the results x = np.linspace(0, 5, 1000)[:, np.newaxis] y_mean, y_cov = gp.predict(x, return_cov=True) plt.figure(figsize=(10, 5)) plt.scatter(X_train, y_train, c='r', label='Training Data') plt.plot(x, y_mean, 'k', lw=2, zorder=9, label='Predicted Mean') plt.fill_between(x[:, 0], y_mean - 1.96 * np.sqrt(np.diag(y_cov)), y_mean + 1.96 * np.sqrt(np.diag(y_cov)), alpha=0.2, color='k', label='95% Confidence Interval') plt.xlabel('X') plt.ylabel('y') plt.legend() plt.show()> Sortir:
Dans ce code, générez d'abord quelques exemples de points de données avec du bruit ajouté, puis définissez un noyau RBF et créez un Régresseur de processus gaussien avec ça. Le modèle est entraîné sur les données d'entraînement et utilisé pour faire des prédictions sur les données de test. Enfin, les résultats sont visualisés avec un graphique montrant les données d'entraînement, la moyenne prédite et l'intervalle de confiance à 95 %.
Implémentation du processus gaussien en Python
Scikit Apprendre
Python import matplotlib.pyplot as plt import numpy as np from scipy import linalg from sklearn.gaussian_process import kernels,GaussianProcessRegressor ## check version import sys import sklearn print(sys.version) !python --version print("numpy:", np.__version__) print("sklearn:",sklearn.__version__)> Les bibliothèques nécessaires à la régression du processus gaussien (GPR) en Python sont importées par ce code ; ceux-ci sont SciPy pour les fonctions d'algèbre linéaire, NumPy pour les opérations numériques, et Matplotlib pour la visualisation des données. Pour s'assurer qu'il est compatible avec les packages nécessaires, il vérifie en outre la version de Python et l'imprime, ainsi que les versions de NumPy et scikit-learn (sklearn).
Sélection du noyau
Python np.random.seed(0) n=50 kernel_ =[kernels.RBF (), kernels.RationalQuadratic(), kernels.ExpSineSquared(periodicity=10.0), kernels.DotProduct(sigma_0=1.0)**2, kernels.Matern() ] print(kernel_, '
')> Sortir:
[RBF(longueur_échelle=1),
RationalQuadratic(alpha=1, length_scale=1),
ExpSineSquared(length_scale=1, périodicité=10),
DotProduct(sigma_0=1) ** 2,
Maternel(length_scale=1, nu=1.5)]
Le code précise le nombre de sites de test (n) et initialise un graine aléatoire . Afin d'afficher les noyaux choisis, il génère une liste de plusieurs fonctions du noyau et imprime la liste.
Comparaison et visualisation du noyau
Python for kernel in kernel_: # Gaussian process gp = GaussianProcessRegressor(kernel=kernel) # Prior x_test = np.linspace(-5, 5, n).reshape(-1, 1) mu_prior, sd_prior = gp.predict(x_test, return_std=True) samples_prior = gp.sample_y(x_test, 3) # plot plt.figure(figsize=(10, 3)) plt.subplot(1, 2, 1) plt.plot(x_test, mu_prior) plt.fill_between(x_test.ravel(), mu_prior - sd_prior, mu_prior + sd_prior, color='aliceblue') plt.plot(x_test, samples_prior, '--') plt.title('Prior') # Fit x_train = np.array([-4, -3, -2, -1, 1]).reshape(-1, 1) y_train = np.sin(x_train) gp.fit(x_train, y_train) # posterior mu_post, sd_post = gp.predict(x_test, return_std=True) mu_post = mu_post.reshape(-1) samples_post = np.squeeze(gp.sample_y(x_test, 3)) # plot plt.subplot(1, 2, 2) plt.plot(x_test, mu_post) plt.fill_between(x_test.ravel(), mu_post - sd_post, mu_post + sd_post, color='aliceblue') plt.plot(x_test, samples_post, '--') plt.scatter(x_train, y_train, c='blue', s=50) plt.title('Posterior') plt.show() print("gp.kernel_", gp.kernel_) print("gp.log_marginal_likelihood:", gp.log_marginal_likelihood(gp.kernel_.theta)) print('-'*50, '
')> Sortir:
FBR
gp.kernel_RBF(length_scale=1.93)
gp.log_marginal_likelihood : -3.444937833462133
-------------------------------------------------- -
Quadratique rationnelle

gp.kernel_ RationalQuadratic(alpha=1e+05, length_scale=1.93)
gp.log_marginal_likelihood : -3.4449718909150966
--------------------------------------------------
ExpSineCarré

gp.kernel_ ExpSineSquared(length_scale=0.000524, périodicité=2.31e+04)
gp.log_marginal_likelihood : -3.4449381454930217
--------------------------------------------------
Produit scalaire

gp.kernel_DotProduct(sigma_0=0.998) ** 2
gp.log_marginal_likelihood : -150204291.56018084
--------------------------------------------------
Maternel

gp.kernel_Matern(length_scale=1,99, nu=1,5)
gp.log_marginal_likelihood : -5.131637070524745
--------------------------------------------------
Le code commence par parcourir les différentes fonctions du noyau répertoriées dans la liste kernel_. Un régresseur de processus gaussien (gp) est créé en utilisant le noyau particulier pour chaque noyau. Pour le processus gaussien, cela établit la structure de covariance. Afin d'évaluer la distribution précédente, un ensemble de points d'entrée de test appelé x_test est établi, avec des valeurs allant de -5 à 5. Cet ensemble de points est transformé en un vecteur colonne.
À l'aide de la méthode gp.predict, la moyenne (mu_prior) et l'écart type (sd_prior) de la distribution a priori sont déterminés à chaque point de test. Les valeurs d’écart type sont demandées à l’aide de l’option return_std=True. gp.sample_y (x_test, 3) est utilisé pour obtenir trois exemples de fonctions de la distribution précédente.
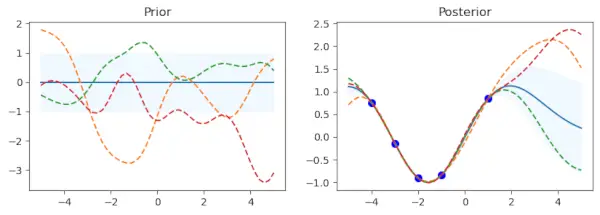
Le premier sous-tracé montre la moyenne de la distribution précédente, l’écart type étant représenté par une zone ombrée. Les échantillons sont superposés sous forme de lignes pointillées, tandis que la moyenne est affichée sous forme de ligne continue. Il y a une intrigue secondaire appelée Prior. Il existe un ensemble défini de points de données d'entraînement (x_train) et de valeurs d'objectifs (y_train) qui les accompagnent. Le modèle de processus gaussien est ajusté à l'aide de ces points (gp.fit(x_train, y_train)). Cinq points de données avec les valeurs sinusoïdales correspondantes constituent les données d'entraînement dans ce code.
Après la phase d'ajustement des données d'entraînement, la procédure calcule la moyenne (mu_post) et l'écart type (sd_post) de la distribution postérieure pour les mêmes points de test (x_test). gp.sample_y(x_test, 3) est également utilisé pour produire des échantillons de fonctions à partir de la distribution postérieure. Le deuxième sous-tracé recouvre les fonctions échantillonnées sous forme de lignes pointillées et montre la moyenne de la distribution a posteriori, ombrée avec l'écart type. Les points de données d'entraînement sont tracés en bleu. L'intrigue secondaire porte le nom Posterior.
Pour voir les tracés précédent et postérieur du noyau actuel et acquérir une compréhension visuelle du comportement du modèle, appelez la fonction plt.show() de Matplotlib.
Le code affiche des détails sur le noyau actuel, tels que gp.kernel_, qui indique le noyau actuel utilisé, et gp.log_marginal_likelihood (gp.kernel_.theta), qui donne le log de vraisemblance marginale du modèle utilisant le noyau actuel, après chaque ensemble de tracés antérieurs et postérieurs.
Avantages de la régression du processus gaussien (GPR)
La régression du processus gaussien (GPR) présente un certain nombre d'avantages dans une gamme d'applications :
- GPR fournit un cadre probabiliste pour la régression, ce qui signifie qu'il donne non seulement des estimations ponctuelles, mais également des estimations d'incertitude pour les prédictions.
- Il est très flexible et peut capturer des relations complexes dans les données.
- Le GPR peut être adapté à diverses applications, notamment la prévision de séries chronologiques, l'optimisation et l'optimisation bayésienne.
Défis de la régression du processus gaussien (GPR)
- Le GPR peut être coûteux en termes de calcul lorsqu'il s'agit de grands ensembles de données, car l'inversion d'une matrice de covariance est nécessaire.
- Le choix de la fonction noyau et de ses hyperparamètres peut avoir un impact significatif sur les performances du modèle.
Bons exemples d'applications GPR
- Prévision du cours des actions : Le GPR peut être utilisé pour modéliser et prédire les cours des actions, en tenant compte de la volatilité et de l'incertitude des marchés financiers.
- Expériences informatiques : Le GPR est utile pour optimiser des simulations complexes en modélisant les relations entrées-sorties et en identifiant les paramètres les plus influents.
- Détection d'une anomalie: Le GPR peut être appliqué à la détection d’anomalies, où il identifie des modèles inhabituels dans les données de séries chronologiques en capturant les distributions normales de données.
Conclusion
En conclusion, la régression du processus gaussien est un outil précieux pour l’analyse des données et la prévision dans les situations où la compréhension de l’incertitude des prédictions est essentielle. En tirant parti de la modélisation probabiliste et des fonctions du noyau, GPR peut fournir des résultats précis et interprétables. Cependant, il est crucial de prendre en compte le coût de calcul et la nécessité de faire appel à des experts lors de la mise en œuvre du GPR dans la pratique.
