Étant donné une matrice carrée avec[][] de commande n votre tâche est de vérifier s'il s'agit d'une matrice Toeplitz.
Note: Une matrice de Toeplitz - également appelée matrice diagonale constante - est une matrice dans laquelle les éléments de chaque diagonale descendante individuelle sont les mêmes de gauche à droite. De manière équivalente pour tout tapis d'entrée[i][j], c'est la même chose que mat[i-1][j-1] ou mat[i-2][j-2] et fils.
Exemples :
nombre aléatoire Java
Saisir: avec[][] = [ [6 7 8]
[4 6 7]
[1 4 6] ]
Sortir: Oui
Explication: Toutes les diagonales de la matrice donnée sont [6 6 6] [7 7] [8] [4 4] [1]. Pour chaque diagonale, comme tous les éléments sont identiques, la matrice donnée est la matrice de Toeplitz.Saisir: avec[][] = [ [6 3 8]
[4 9 7]
[1 4 6] ]
Sortir: Non
Explication: Les principaux éléments diagonaux de la matrice donnée sont [6 9 6]. Comme les éléments diagonaux ne sont pas les mêmes, la matrice donnée n'est pas la matrice de Toeplitz.
[Approche attendue - 1] - Vérification de chaque diagonale - O(n * n) Temps et O(1) Espace
L'idée est de parcourir chaque diagonale descendante de la matrice en utilisant chaque élément de la première ligne et chaque élément de la première colonne comme point de départ et de vérifier que chaque élément le long de cette diagonale correspond à la valeur en tête.
liste de tableaux triée en Java
Suivez les étapes ci-dessous :
- Laisser
n = mat.size()etm = mat[0].size(). - Pour chaque index de colonne
idepuis0àm - 1appelcheckDiagonal(mat 0 i); s'il renvoie faux, renvoie immédiatement faux deisToeplitz. - Pour chaque index de ligne
idepuis0àn - 1appelcheckDiagonal(mat i 0); s'il renvoie faux, renvoie immédiatement faux deisToeplitz. - Si tous les appels à
checkDiagonalréussir, retourner vrai. - Dans
checkDiagonal(mat x y)comparermat[i][j]àmat[x][y]pour chacuni = x+1 j = y+1alors quei < n && j < m; renvoie false au premier décalage, sinon renvoie true après avoir atteint le bord.
Ci-dessous est donné le mise en œuvre:
C++#include
import java.util.*; class GfG { // function to check if diagonal elements are same static boolean checkDiagonal(List<List<Integer>> mat int x int y) { int n = mat.size() m = mat.get(0).size(); for(int i = x + 1 j = y + 1; i < n && j < m; i++ j++) { if(!mat.get(i).get(j).equals(mat.get(x).get(y))) return false; } return true; } // Function to check whether given // matrix is toeplitz matrix or not static boolean isToeplitz(List<List<Integer>> mat) { int n = mat.size() m = mat.get(0).size(); // check each descending diagonal starting from // first row and first column of the matrix for(int i = 0; i < m; i++) if(!checkDiagonal(mat 0 i)) return false; for(int i = 0; i < n; i++) if(!checkDiagonal(mat i 0)) return false; // if all diagonals are same return true return true; } public static void main(String[] args) { List<List<Integer>> mat = Arrays.asList( Arrays.asList(6 7 8) Arrays.asList(4 6 7) Arrays.asList(1 4 6) ); if(isToeplitz(mat)) { System.out.println('Yes'); } else { System.out.println('No'); } } }
# function to check if diagonal elements are same def checkDiagonal(mat x y): n m = len(mat) len(mat[0]) i j = x + 1 y + 1 while i < n and j < m: if mat[i][j] != mat[x][y]: return False i += 1 j += 1 return True # Function to check whether given # matrix is toeplitz matrix or not def isToeplitz(mat): n m = len(mat) len(mat[0]) # check each descending diagonal starting from # first row and first column of the matrix for i in range(m): if not checkDiagonal(mat 0 i): return False for i in range(n): if not checkDiagonal(mat i 0): return False # if all diagonals are same return true return True mat = [ [6 7 8] [4 6 7] [1 4 6] ] if isToeplitz(mat): print('Yes') else: print('No')
using System; using System.Collections.Generic; class GfG { // function to check if diagonal elements are same static bool checkDiagonal(List<List<int>> mat int x int y) { int n = mat.Count m = mat[0].Count; for(int i = x + 1 j = y + 1; i < n && j < m; i++ j++) { if(mat[i][j] != mat[x][y]) return false; } return true; } // Function to check whether given // matrix is toeplitz matrix or not static bool isToeplitz(List<List<int>> mat) { int n = mat.Count m = mat[0].Count; // check each descending diagonal starting from // first row and first column of the matrix for(int i = 0; i < m; i++) if(!checkDiagonal(mat 0 i)) return false; for(int i = 0; i < n; i++) if(!checkDiagonal(mat i 0)) return false; // if all diagonals are same return true return true; } static void Main() { var mat = new List<List<int>> { new List<int> {6 7 8} new List<int> {4 6 7} new List<int> {1 4 6} }; if(isToeplitz(mat)) { Console.WriteLine('Yes'); } else { Console.WriteLine('No'); } } }
// function to check if diagonal elements are same function checkDiagonal(mat x y) { let n = mat.length m = mat[0].length; for(let i = x + 1 j = y + 1; i < n && j < m; i++ j++) { if(mat[i][j] !== mat[x][y]) return false; } return true; } // Function to check whether given // matrix is toeplitz matrix or not function isToeplitz(mat) { let n = mat.length m = mat[0].length; // check each descending diagonal starting from // first row and first column of the matrix for(let i = 0; i < m; i++) if(!checkDiagonal(mat 0 i)) return false; for(let i = 0; i < n; i++) if(!checkDiagonal(mat i 0)) return false; // if all diagonals are same return true return true; } let mat = [ [6 7 8] [4 6 7] [1 4 6] ]; if(isToeplitz(mat)) { console.log('Yes'); } else { console.log('No'); }
Sortir
Yes
[Approche attendue - 2] - Vérification en diagonale au-dessus de l'élément - O(n * n) Temps et O(1) Espace
L'idée est d'analyser chaque cellule à partir de la deuxième ligne et de la deuxième colonne en comparant chaque valeur à sa voisine en haut à gauche. Si un élément diffère de celui situé en diagonale au-dessus, vous avez constaté une violation de la propriété Toeplitz et pouvez vous arrêter immédiatement ; si vous parcourez toute la matrice sans décalage, chaque diagonale est constante.
Suivez les étapes ci-dessous :
- Laisser
n = mat.size()etm = mat[0].size(). - Répéter
ide 1 àn - 1et à l'intérieur de celajde 1 àm - 1. - Si
mat[i][j] != mat[i - 1][j - 1]à tout moment revenirfalse. - Une fois que toutes les paires ont été vérifiées sans discordance, retournez
true.
Ci-dessous est donné le mise en œuvre:
C++#include
import java.util.*; class GfG { // Function to check whether given // matrix is toeplitz matrix or not static boolean isToeplitz(List<List<Integer>> mat) { int n = mat.size() m = mat.get(0).size(); // check diagonally above element of // each element in the matrix for(int i = 1; i < n; i++) { for(int j = 1; j < m; j++) { if(mat.get(i).get(j) != mat.get(i - 1).get(j - 1)) return false; } } // if all diagonals are same return true return true; } public static void main(String[] args) { List<List<Integer>> mat = Arrays.asList( Arrays.asList(6 7 8) Arrays.asList(4 6 7) Arrays.asList(1 4 6) ); if(isToeplitz(mat)) { System.out.println('Yes'); } else { System.out.println('No'); } } }
# Function to check whether given # matrix is toeplitz matrix or not def isToeplitz(mat): n m = len(mat) len(mat[0]) # check diagonally above element of # each element in the matrix for i in range(1 n): for j in range(1 m): if mat[i][j] != mat[i - 1][j - 1]: return False # if all diagonals are same return true return True mat = [ [6 7 8] [4 6 7] [1 4 6] ] if isToeplitz(mat): print('Yes') else: print('No')
using System; using System.Collections.Generic; class GfG { // Function to check whether given // matrix is toeplitz matrix or not static bool isToeplitz(List<List<int>> mat) { int n = mat.Count m = mat[0].Count; // check diagonally above element of // each element in the matrix for(int i = 1; i < n; i++) { for(int j = 1; j < m; j++) { if(mat[i][j] != mat[i - 1][j - 1]) return false; } } // if all diagonals are same return true return true; } static void Main() { var mat = new List<List<int>> { new List<int> {6 7 8} new List<int> {4 6 7} new List<int> {1 4 6} }; if(isToeplitz(mat)) { Console.WriteLine('Yes'); } else { Console.WriteLine('No'); } } }
// Function to check whether given // matrix is toeplitz matrix or not function isToeplitz(mat) { let n = mat.length m = mat[0].length; // check diagonally above element of // each element in the matrix for(let i = 1; i < n; i++) { for(let j = 1; j < m; j++) { if(mat[i][j] !== mat[i - 1][j - 1]) return false; } } // if all diagonals are same return true return true; } let mat = [ [6 7 8] [4 6 7] [1 4 6] ]; if(isToeplitz(mat)) { console.log('Yes'); } else { console.log('No'); }
Sortir
Yes
[Approche alternative] - Utilisation du hachage - O(n * n) Temps et O(n) Espace
L'idée est d'attribuer un identifiant unique à chaque diagonale inférieure droite (l'index de ligne moins l'index de colonne) et d'utiliser une carte de hachage pour enregistrer la première valeur vue pour cette diagonale. Lorsque vous analysez la matrice entière, vous calculez cette clé pour chaque cellule et vérifiez qu'elle correspond à la valeur stockée ou si elle est nouvelle, stockez-la. Une seule inadéquation vous permet de vous en sortir avec false ; sinon vous concluez vrai à la fin.
Suivez les étapes ci-dessous :
- Déterminez les dimensions de la matrice (nombre de lignes et nombre de colonnes) à partir de
mat. - Créer une hashmap vide
mppour mapper chaque touche diagonale à sa valeur représentative. - Parcourez chaque cellule de
matpar son index de ligneiet index de colonnej. - Pour chaque cellule, formez la clé diagonale en soustrayant
jdepuisi. - Si
mpdétient déjà cette clé, compare l'élément actuel à la valeur stockée ; s'ils diffèrent, retournez false immédiatement. - Si la clé n'est pas encore insérée
mpenregistrez l'élément actuel sous cette clé. - Si vous terminez le parcours sans aucune incompatibilité, renvoyez true.
Illustration:
Java a la suite
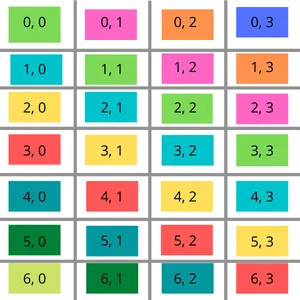
Le diagramme ci-dessous donne une meilleure visualisation de cette idée. Considérez la diagonale de couleur jaune. La différence entre la valeur x et la valeur y de tout indice sur cette diagonale est de 2 (2-0 3-1 4-2 5-3). La même chose peut être observée pour toutes les diagonales du corps.
Pour la couleur rouge, la différence diagonale est de 3. Pour la couleur verte, la différence diagonale est de 0. Pour la couleur orange, la différence diagonale est de -2 et ainsi de suite...
Ci-dessous est donné le mise en œuvre:
C++#include
// JAVA program to check whether given matrix // is a Toeplitz matrix or not import java.util.*; class GFG { static boolean isToeplitz(int[][] matrix) { // row = number of rows // col = number of columns int row = matrix.length; int col = matrix[0].length; // HashMap to store keyvalue pairs HashMap<Integer Integer> map = new HashMap<Integer Integer>(); for (int i = 0; i < row; i++) { for (int j = 0; j < col; j++) { int key = i - j; // if key value exists in the hashmap if (map.containsKey(key)) { // we check whether the current value // stored in this key matches to element // at current index or not. If not // return false if (map.get(key) != matrix[i][j]) return false; } // else we put keyvalue pair in hashmap else { map.put(i - j matrix[i][j]); } } } return true; } // Driver Code public static void main(String[] args) { int[][] matrix = { { 12 23 -32 } { -20 12 23 } { 56 -20 12 } { 38 56 -20 } }; // Function call String result = (isToeplitz(matrix)) ? 'Yes' : 'No'; System.out.println(result); } }
# Python3 program to check whether given matrix # is a Toeplitz matrix or not def isToeplitz(matrix): # row = number of rows # col = number of columns row = len(matrix) col = len(matrix[0]) # dictionary to store keyvalue pairs map = {} for i in range(row): for j in range(col): key = i-j # if key value exists in the map if (key in map): # we check whether the current value stored # in this key matches to element at current # index or not. If not return false if (map[key] != matrix[i][j]): return False # else we put keyvalue pair in map else: map[key] = matrix[i][j] return True # Driver Code if __name__ == '__main__': matrix = [[12 23 -32] [-20 12 23] [56 -20 12] [38 56 -20]] # Function call if (isToeplitz(matrix)): print('Yes') else: print('No')
using System; using System.Collections.Generic; class GfG { // Function to check whether given // matrix is toeplitz matrix or not static bool isToeplitz(List<List<int>> mat) { int n = mat.Count m = mat[0].Count; // HashMap to store keyvalue pairs Dictionary<intint> mp = new Dictionary<intint>(); for(int i = 0; i < n; i++) { for(int j = 0; j < m; j++) { int key = i - j; // If key value exists in the hashmap if (mp.ContainsKey(key)) { // check if the value is same // as the current element if (mp[key] != mat[i][j]) return false; } // Else we put keyvalue pair in hashmap else { mp[i - j] = mat[i][j]; } } } return true; } static void Main() { var mat = new List<List<int>> { new List<int> {6 7 8} new List<int> {4 6 7} new List<int> {1 4 6} }; if(isToeplitz(mat)) { Console.WriteLine('Yes'); } else { Console.WriteLine('No'); } } }
// Function to check whether given // matrix is toeplitz matrix or not function isToeplitz(mat) { let n = mat.length m = mat[0].length; // HashMap to store keyvalue pairs const mp = new Map(); for(let i = 0; i < n; i++) { for(let j = 0; j < m; j++) { let key = i - j; // If key value exists in the hashmap if (mp.has(key)) { // check if the value is same // as the current element if (mp.get(key) !== mat[i][j]) return false; } // Else we put keyvalue pair in hashmap else { mp.set(i - j mat[i][j]); } } } return true; } let mat = [ [6 7 8] [4 6 7] [1 4 6] ]; if(isToeplitz(mat)) { console.log('Yes'); } else { console.log('No'); }
Sortir
Yes