Un encodeur est un circuit numérique qui convertit un ensemble d'entrées binaires en un code binaire unique. Le code binaire représente la position de l'entrée et est utilisé pour identifier l'entrée spécifique qui est active. Les encodeurs sont couramment utilisés dans les systèmes numériques pour convertir un ensemble parallèle d'entrées en un code série.
Le principe de base d'un codeur est d'attribuer un code binaire unique à chaque entrée possible. Par exemple, un encodeur de 2 à 4 lignes possède 2 lignes d'entrée et 4 lignes de sortie et attribue un code binaire unique de 4 bits à chacune des 2 ^ 2 = 4 combinaisons d'entrée possibles. La sortie d'un codeur est généralement active faible, ce qui signifie qu'une seule sortie est active (faible) à un moment donné et les sorties restantes sont inactives (élevées). La sortie basse active est sélectionnée en fonction du code binaire attribué à l'entrée active.
tests de logiciels
Il existe différents types d'encodeurs, notamment les encodeurs prioritaires, qui attribuent une priorité à chaque entrée, et les encodeurs à pondération binaire, qui utilisent un système de pondération binaire pour attribuer des codes binaires aux entrées. En résumé, un encodeur est un circuit numérique qui convertit un ensemble d'entrées binaires en un code binaire unique représentant la position de l'entrée. Les encodeurs sont largement utilisés dans les systèmes numériques pour convertir les entrées parallèles en codes série.
Un encodeur est un circuit combinatoire qui effectue l'opération inverse d'un Décodeur . Il a un maximum de 2 ^ n lignes d'entrée et 'n' lignes de sortie , il code donc les informations de 2 ^ n entrées dans un code à n bits. Il produira un code binaire équivalent à l’entrée, qui est active High. Par conséquent, l’encodeur code 2 ^ n lignes d’entrée avec « n » bits.
Encodeur
Types d'encodeurs
Il existe différents types d'encodeurs mentionnés ci-dessous.
- Encodeur 4 à 2
- Encodeur octal à binaire (encodeur 8 à 3)
- Encodeur décimal vers BCD
- Encodeur prioritaire
Encodeur 4 à 2
L'encodeur 4 à 2 se compose de quatre entrées Y3, Y2, Y1 et Y0 et deux sorties A1 et A0 . A tout moment, une seule de ces 4 entrées peut être à « 1 » afin d’obtenir en sortie le code binaire respectif. La figure ci-dessous montre le symbole logique de l'encodeur 4 à 2.
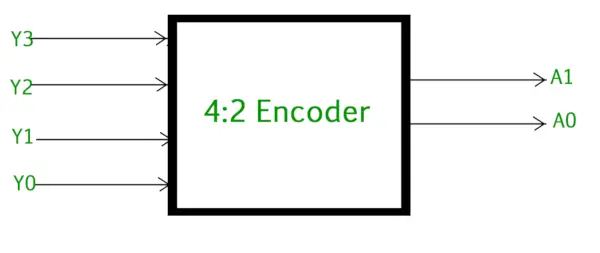
Encodeur 4 à 2
La table de vérité de 4 à 2 encodeurs est la suivante.
| CONTRIBUTIONS | LES SORTIES | ||||
|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
Expression logique pour A1 et A0 :
A1 = Y3 + Y2 A0 = Y3 + Y1>
Les deux fonctions booléennes A1 et A0 ci-dessus peuvent être implémentées à l'aide de deux portes OU d'entrée :
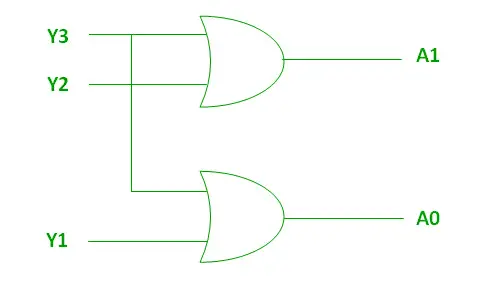
Implémentation à l'aide de OR Gate
Encodeur octal à binaire (encodeur 8 à 3)
L'encodeur 8 à 3 ou l'encodeur octal vers binaire se compose de 8 entrées : Y7 à Y0 et 3 sorties : A2, A1 et A0. Chaque ligne d'entrée correspond à chaque chiffre octal et trois sorties génèrent le code binaire correspondant. La figure ci-dessous montre le symbole logique de l'octal pour l'encodeur binaire.
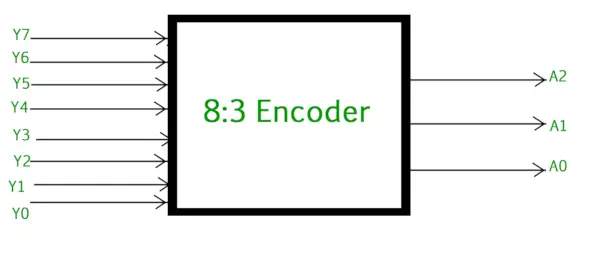
Encodeur octal à binaire (encodeur 8 à 3)
La table de vérité pour l'encodeur 8 à 3 est la suivante.
| CONTRIBUTIONS | LES SORTIES | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 | A2 | A1 | A0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
Expression logique pour A2, A1 et A0.
A2 = Y7 + Y6 + Y5 + Y4 A1 = Y7 + Y6 + Y3 + Y2 A0 = Y7 + Y5 + Y3 + Y1>
Les deux fonctions booléennes A2, A1 et A0 ci-dessus peuvent être implémentées à l'aide de quatre entrées. OU portes .
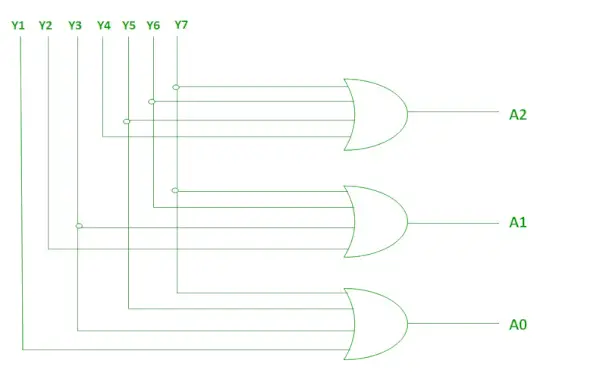
Implémentation à l'aide de OR Gate
Encodeur décimal vers BCD
L'encodeur décimal-binaire se compose généralement de 10 lignes d'entrée et 4 lignes de sortie . Chaque ligne d'entrée correspond à chaque chiffre décimal et 4 sorties correspondent au code BCD. Cet encodeur accepte les données décimales décodées comme entrée et les code vers la sortie BCD qui est disponible sur les lignes de sortie. La figure ci-dessous montre le symbole logique de l'encodeur décimal vers BCD :
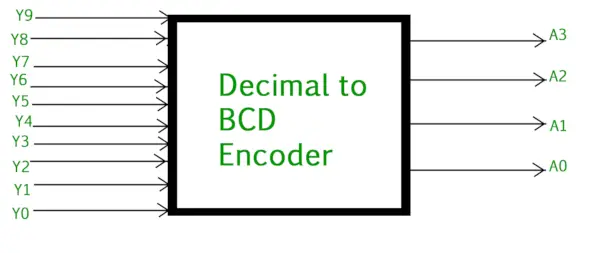
Encodeur décimal vers BCD
La table de vérité pour décimal à Encodeur BCD est comme suit.
| CONTRIBUTIONS | LES SORTIES | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Y9 | Y8 | Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 | A3 | A2 | A1 | A0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
Expression logique pour A3, A2, A1 et A0.
A3 = Y9 + Y8 A2 = Y7 + Y6 + Y5 +Y4 A1 = Y7 + Y6 + Y3 +Y2 A0 = Y9 + Y7 +Y5 +Y3 + Y1>
Les deux fonctions booléennes ci-dessus peuvent être implémentées à l’aide de portes OU.
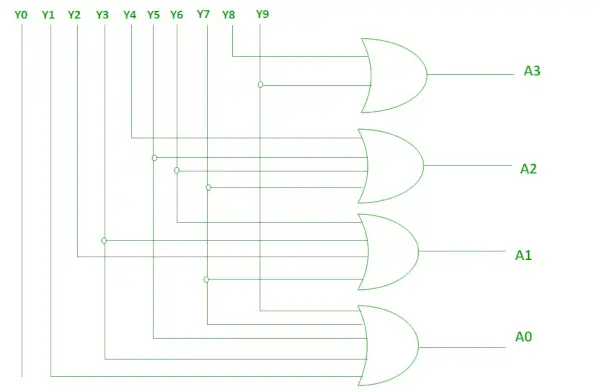
Implémentation à l'aide de OR Gate
Encodeur prioritaire
Un encodeur de priorité 4 à 2 a 4 entrées : Y3, Y2, Y1 et Y0, et 2 sorties : A1 et A0. Ici, l'entrée Y3 a le priorité la plus élevée , alors que l'entrée Y0 a le priorité la plus basse . Dans ce cas, même si plusieurs entrées sont à « 1 » en même temps, la sortie sera le code (binaire) correspondant à l'entrée, qui a priorité plus élevée . La table de vérité du codeur prioritaire est la suivante.
| CONTRIBUTIONS | LES SORTIES | |||||
|---|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 | DANS |
| 0 | 0 | 0 | 0 | X | X | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | X | 0 | 1 | 1 |
| 0 | 1 | X | X | 1 | 0 | 1 |
| 1 | X | X | X | 1 | 1 | 1 |
L’expression logique de A1 est présentée ci-dessous.
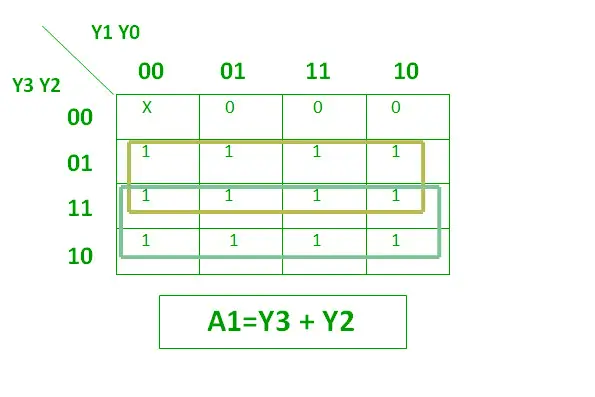
Expression logique
L'expression logique pour A0 est présentée ci-dessous.
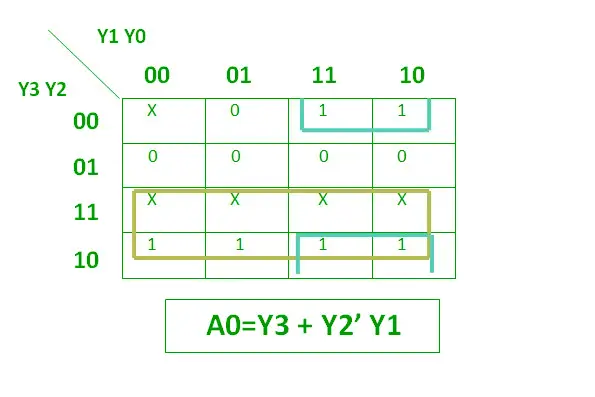
Expression logique
Les deux fonctions booléennes ci-dessus peuvent être implémentées comme.
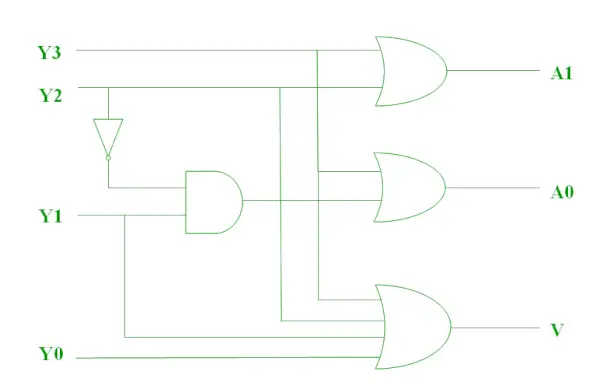
Encodeur prioritaire
Certaines erreurs qui se produisent généralement dans les encodeurs sont mentionnées ci-dessous.
- Il existe une ambiguïté lorsque toutes les sorties du codeur sont égales à zéro.
- Si plus d’une entrée est active High, alors l’encodeur produit une sortie, qui peut ne pas être le bon code.
Ainsi, pour surmonter ces difficultés, il convient d'attribuer des priorités à chaque entrée de l'encodeur. Ensuite, la sortie de l'encodeur sera le code correspondant aux entrées actives hautes, qui ont une priorité plus élevée.
Application des encodeurs
- Les encodeurs sont des circuits électroniques très courants utilisés dans tous les systèmes numériques.
- Les encodeurs sont utilisés pour traduire les valeurs décimales en binaire afin d'exécuter des fonctions binaires telles que l'addition, la soustraction, la multiplication, etc.
- D'autres applications, notamment pour les encodeurs prioritaires, peuvent inclure la détection d'interruptions dans les applications de microprocesseur.
Avantages de l'utilisation d'encodeurs en logique numérique
- Réduction du nombre de lignes : Les encodeurs réduisent le nombre de lignes nécessaires pour transmettre les informations de plusieurs entrées vers une seule sortie, ce qui peut simplifier la conception du système et réduire le coût des composants.
- Fiabilité améliorée : En convertissant plusieurs entrées en un seul code série, les encodeurs peuvent réduire le risque d'erreurs dans la transmission des informations.
- Performance améliorée: Les encodeurs peuvent améliorer les performances d'un système numérique en réduisant le temps nécessaire pour transmettre les informations de plusieurs entrées vers une seule sortie.
Inconvénients de l'utilisation d'encodeurs dans la logique numérique
- Complexité accrue : Les codeurs sont généralement des circuits plus complexes que les multiplexeurs , et nécessitent des composants supplémentaires à implémenter.
- Limité à des applications spécifiques : Les encodeurs ne conviennent que pour les applications dans lesquelles un ensemble parallèle d'entrées doit être converti en un code série.
- Flexibilité limitée : Les encodeurs sont limités dans leur flexibilité, car ils ne peuvent encoder qu'un nombre fixe d'entrées dans un nombre fixe de sorties.
- En conclusion, les encodeurs sont des circuits numériques utiles qui présentent des avantages et des inconvénients. Le choix d'utiliser ou non un codeur dépend des exigences spécifiques du système et des compromis entre complexité, fiabilité, performances et coût.
Questions du coin GATE CS
La pratique des questions suivantes vous aidera à tester vos connaissances. Toutes les questions ont été posées dans GATE les années précédentes ou lors de tests simulés GATE. Il est fortement recommandé de les pratiquer.
- GATE CS 2013, question 65
- GATE CS 2014 (ensemble 3), question 65
