L'algorithme vectoriel Distance est itératif, asynchrone et distribué.
Distribué:Il est distribué dans le sens où chaque nœud reçoit des informations d'un ou plusieurs de ses voisins directement attachés, effectue des calculs puis redistribue le résultat à ses voisins.Itératif:Il est itératif dans le sens où son processus se poursuit jusqu'à ce qu'il n'y ait plus d'informations disponibles pour être échangées entre voisins.Asynchrone:Il n’est pas nécessaire que tous ses nœuds fonctionnent dans une étape de verrouillage les uns avec les autres.
• L'algorithme vectoriel Distance est un algorithme dynamique.
• Il est principalement utilisé dans ARPANET et RIP.
• Chaque routeur maintient une table de distance appelée Vecteur .

Trois clés pour comprendre le fonctionnement de l'algorithme de routage à vecteur de distance :

Connaissance de l'ensemble du réseau :Chaque routeur partage ses connaissances sur l'ensemble du réseau. Le routeur envoie ses connaissances collectées sur le réseau à ses voisins.Acheminement uniquement vers les voisins :Le routeur envoie ses connaissances sur le réseau uniquement aux routeurs disposant de liens directs. Le routeur envoie tout ce qu'il a sur le réseau via les ports. Les informations sont reçues par le routeur et les utilisent pour mettre à jour sa propre table de routage.Partage d’informations à intervalles réguliers :Dans les 30 secondes, le routeur envoie les informations aux routeurs voisins.

Algorithme de routage à vecteur de distance

Laissez d_X(y) être le coût du chemin le moins coûteux du nœud x au nœud y. Les moindres coûts sont liés par l'équation de Bellman-Ford,

 d<sub>x</sub>(y) = min<sub>v</sub>{c(x,v) + d<sub>v</sub>(y)} 

Où le minv est l'équation prise pour tous les x voisins. Après avoir parcouru x à v, si l’on considère le chemin le moins coûteux de v à y, le coût du chemin sera c(x,v)+d_dans(oui). Le moindre coût de x à y est le minimum de c(x,v)+d_dans(y) repris tous les voisins.

Avec l'algorithme Distance Vector Routing, le nœud x contient les informations de routage suivantes :

• Pour chaque voisin v, le coût c(x,v) est le coût du chemin de x au voisin directement attaché, v.
• Le vecteur distance x, c'est-à-dire D_X= [ ré_X(y) : y en N ], contenant son coût vers toutes les destinations, y, en N.
• Le vecteur distance de chacun de ses voisins, c'est-à-dire D_dans= [ ré_dans(y) : y dans N ] pour chaque voisin v de x.

Le routage vectoriel de distance est un algorithme asynchrone dans lequel le nœud x envoie la copie de son vecteur de distance à tous ses voisins. Lorsque le nœud x reçoit le nouveau vecteur distance de l'un de ses vecteurs voisins, v, il enregistre le vecteur distance de v et utilise l'équation de Bellman-Ford pour mettre à jour son propre vecteur distance. L'équation est donnée ci-dessous :

conception unique

 d<sub>x</sub>(y) = min<sub>v</sub>{ c(x,v) + d<sub>v</sub>(y)} for each node y in N 

Le nœud x a mis à jour sa propre table de vecteurs de distance en utilisant l'équation ci-dessus et envoie sa table mise à jour à tous ses voisins afin qu'ils puissent mettre à jour leurs propres vecteurs de distance.

Algorithme

 At each node x, <p> <strong>Initialization</strong> </p> for all destinations y in N: D<sub>x</sub>(y) = c(x,y) // If y is not a neighbor then c(x,y) = &#x221E; for each neighbor w D<sub>w</sub>(y) = ? for all destination y in N. for each neighbor w send distance vector D<sub>x</sub> = [ D<sub>x</sub>(y) : y in N ] to w <strong>loop</strong> <strong>wait</strong> (until I receive any distance vector from some neighbor w) for each y in N: D<sub>x</sub>(y) = minv{c(x,v)+D<sub>v</sub>(y)} If D<sub>x</sub>(y) is changed for any destination y Send distance vector D<sub>x</sub> = [ D<sub>x</sub>(y) : y in N ] to all neighbors <strong>forever</strong> 

Remarque : dans l'algorithme vectoriel de distance, le nœud x met à jour sa table lorsqu'il constate un changement de coût dans l'un des nœuds directement liés ou lorsqu'il reçoit une mise à jour vectorielle d'un voisin.

Comprenons à travers un exemple :

Partager des informations

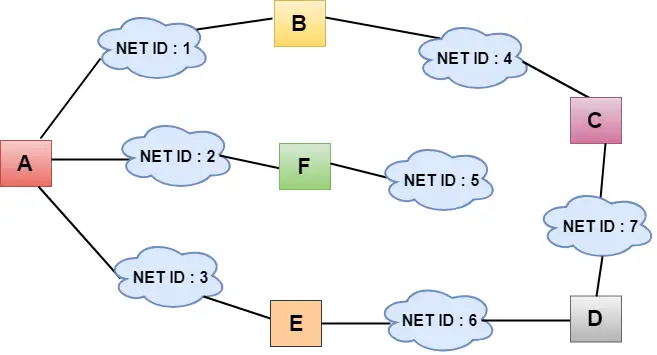
• Dans la figure ci-dessus, chaque cloud représente le réseau et le numéro à l'intérieur du cloud représente l'ID du réseau.
• Tous les réseaux locaux sont connectés par des routeurs et sont représentés dans des cases intitulées A, B, C, D, E, F.
• L'algorithme de routage à vecteur de distance simplifie le processus de routage en supposant que le coût de chaque liaison est d'une unité. Par conséquent, l’efficacité de la transmission peut être mesurée par le nombre de liaisons pour atteindre la destination.
• Dans le routage vectoriel de distance, le coût est basé sur le nombre de sauts.

Dans la figure ci-dessus, nous observons que le routeur envoie la connaissance aux voisins immédiats. Les voisins ajoutent ces connaissances à leurs propres connaissances et envoient la table mise à jour à leurs propres voisins. De cette façon, les routeurs obtiennent leurs propres informations ainsi que les nouvelles informations sur les voisins.

Table de routage

Deux processus se produisent :

• Création du tableau
• Mise à jour du tableau

Création du tableau

Initialement, la table de routage est créée pour chaque routeur et contient au moins trois types d'informations telles que l'ID du réseau, le coût et le prochain saut.

ID RÉSEAU :L'ID réseau définit la destination finale du paquet.Coût:Le coût est le nombre de sauts que le paquet doit effectuer pour y arriver.Saut suivant :C'est le routeur auquel le paquet doit être livré.

• Dans la figure ci-dessus, les tables de routage d'origine sont affichées pour tous les routeurs. Dans une table de routage, la première colonne représente l'ID du réseau, la deuxième colonne représente le coût de la liaison et la troisième colonne est vide.
• Ces tables de routage sont envoyées à tous les voisins.

Par exemple:

 A sends its routing table to B, F & E. B sends its routing table to A & C. C sends its routing table to B & D. D sends its routing table to E & C. E sends its routing table to A & D. F sends its routing table to A. 

Mise à jour du tableau

• Lorsque A reçoit une table de routage de B, il utilise ses informations pour mettre à jour la table.
• La table de routage de B montre comment les paquets peuvent se déplacer vers les réseaux 1 et 4.
• Le B est un voisin du routeur A, les paquets de A à B peuvent atteindre en un seul saut. Ainsi, 1 est ajouté à tous les coûts indiqués dans le tableau B et la somme sera le coût pour atteindre un réseau particulier.

• Après ajustement, A combine ensuite cette table avec sa propre table pour créer une table combinée.

• Le tableau combiné peut contenir des données en double. Dans la figure ci-dessus, la table combinée du routeur A contient les données en double, elle ne conserve donc que les données dont le coût est le plus bas. Par exemple, A peut envoyer les données au réseau 1 de deux manières. Le premier, qui n’utilise aucun routeur suivant, coûte donc un saut. La seconde nécessite deux sauts (A vers B, puis B vers le réseau 1). La première option a le coût le plus bas, elle est donc conservée et la seconde est abandonnée.

• Le processus de création de la table de routage se poursuit pour tous les routeurs. Chaque routeur reçoit les informations des voisins et met à jour la table de routage.

Les tables de routage finales de tous les routeurs sont données ci-dessous :