Le tri par insertion et le tri par sélection sont deux algorithmes de tri populaires, et leur principale différence réside dans la manière dont ils sélectionnent et placent les éléments dans une séquence triée.
Tri de sélection :
- Dans le tri par sélection, le tableau d'entrée est divisé en deux parties : une partie triée et une partie non triée.
- L'algorithme trouve à plusieurs reprises l'élément minimum dans la partie non triée et l'échange avec l'élément le plus à gauche de la partie non triée, étendant ainsi la partie triée d'un élément.
- Le tri par sélection a une complexité temporelle de O(n^2) dans tous les cas.
Tri par insertion:
- Dans le tri par insertion, le tableau d'entrée est également divisé en deux parties : une partie triée et une partie non triée.
L'algorithme récupère un élément de la partie non triée et le place à la position correcte dans la partie triée, en décalant les éléments les plus gros d'une position vers la droite.
Le tri par insertion a une complexité temporelle de O(n^2) dans le pire des cas, mais peut mieux fonctionner sur des tableaux partiellement triés, avec une complexité temporelle dans le meilleur des cas de O(n).
Principales différences : - Le tri par sélection analyse la partie non triée pour trouver l'élément minimum, tandis que le tri par insertion analyse la partie triée pour trouver la position correcte pour placer l'élément.
Le tri par sélection nécessite moins d'échanges que le tri par insertion, mais plus de comparaisons.
Le tri par insertion est plus efficace que le tri par sélection lorsque le tableau d'entrée est partiellement ou presque trié, tandis que le tri par sélection fonctionne mieux lorsque le tableau est très peu trié.
En résumé, les deux algorithmes ont une complexité temporelle similaire, mais leurs méthodes de sélection et de placement diffèrent. Le choix entre eux dépend des caractéristiques des données d’entrée et des exigences spécifiques du problème à résoudre.
Avantages du tri par insertion :
- Simple et facile à comprendre et à mettre en œuvre.
- Efficace pour les petits ensembles de données ou les données presque triées.
- Algorithme de tri sur place, ce qui signifie qu’il ne nécessite pas de mémoire supplémentaire.
- Algorithme de tri stable, ce qui signifie qu'il maintient l'ordre relatif des éléments égaux dans le tableau d'entrée.
Inconvénients du tri par insertion :
- Inefficace pour les grands ensembles de données ou les données ordonnées inversement, avec une complexité temporelle dans le pire des cas de O(n^2).
- Le tri par insertion comporte de nombreux swaps, ce qui peut le ralentir sur les ordinateurs modernes.
Avantages du tri par sélection :
- Simple et facile à comprendre et à mettre en œuvre.
- Efficace pour les petits ensembles de données ou les données presque triées.
- Algorithme de tri sur place, ce qui signifie qu’il ne nécessite pas de mémoire supplémentaire.
Inconvénients du tri par sélection :
- Inefficace pour les grands ensembles de données, avec une complexité temporelle dans le pire des cas de O(n^2).
- Le tri par sélection comporte de nombreuses comparaisons, ce qui peut le ralentir sur les ordinateurs modernes.
- Algorithme de tri instable, ce qui signifie qu'il peut ne pas maintenir l'ordre relatif des éléments égaux dans le tableau d'entrée.
Dans cet article, nous aborderons la différence entre le tri par Insertion et le tri par Sélection :
Tri par insertion est un algorithme de tri simple qui fonctionne de la même manière que vous triez les cartes à jouer entre vos mains. Le tableau est virtuellement divisé en une partie triée et une partie non triée. Les valeurs de la pièce non triée sont sélectionnées et placées à la position correcte dans la pièce triée.
Algorithme:
Pour trier un tableau de taille n par ordre croissant :
- Itérer de arr[1] à arr[n] sur le tableau.
- Comparez l'élément actuel (clé) à son prédécesseur.
- Si l'élément clé est plus petit que son prédécesseur, comparez-le aux éléments précédents. Déplacez les éléments les plus grands d'une position vers le haut pour libérer de l'espace pour l'élément échangé.
Vous trouverez ci-dessous l'image pour illustrer le tri par insertion :
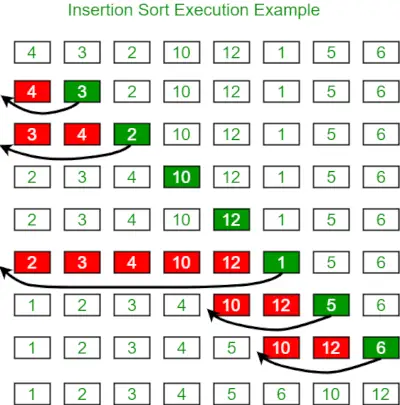
Ci-dessous le programme correspondant :
C++
// C++ program for the insertion sort> #include> using> namespace> std;> // Function to sort an array using> // insertion sort> void> insertionSort(>int> arr[],>int> n)> {> >int> i, key, j;> >for> (i = 1; i key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> clé) { arr[j + 1] = arr[j]; j = j - 1 ; } arr[j + 1] = clé ; } } // Fonction pour imprimer un tableau de taille N void printArray(int arr[], int n) { int i; // Imprime le tableau pour (i = 0; je coute<< arr[i] << ' '; } cout << endl; } // Driver Code int main() { int arr[] = { 12, 11, 13, 5, 6 }; int N = sizeof(arr) / sizeof(arr[0]); // Function Call insertionSort(arr, N); printArray(arr, N); return 0; }> |
>
>
Java
// Java program for the above approach> import> java.util.*;> class> GFG> {> > // Function to sort an array using> // insertion sort> static> void> insertionSort(>int> arr[],>int> n)> {> >int> i, key, j;> >for> (i =>1>; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> clé) { arr[j + 1] = arr[j]; j = j - 1 ; } arr[j + 1] = clé ; } } // Fonction pour imprimer un tableau de taille N static void printArray(int arr[], int n) { int i; // Imprime le tableau pour (i = 0; i System.out.print(arr[i] + ' '); } System.out.println(); } // Code du pilote public static void main(String[ ] args) { int arr[] = { 12, 11, 13, 5, 6 }; int N = arr.length; // Appel de fonction insertionSort(arr, N); Ce code est fourni par code_hunt>'>. |
>
# Python 3 program for the insertion sort># Function to sort an array using># insertion sort>def>insertionSort(arr, n):>>i>=>0>>key>=>0>>j>=>0>>for>i>in>range>(>1>,n,>1>):>>key>=>arr[i]>>j>=>i>->1>># Move elements of arr[0..i-1],>># that are greater than key to>># one position ahead of their>># current position>>while>(j>>=>0>and>arr[j]>clé):>>arr[j>+>1>]>=>arr[j]>>j>=>j>->1>>arr[j>+>1>]>=>key># Function to print an array of size N>def>printArray(arr, n):>>i>=>0>># Print the array>>for>i>in>range>(n):>>print>(arr[i],end>=>' '>)>>print>(>' '>,end>=>'')># Driver Code>if>__name__>=>=>'__main__'>:>>arr>=>[>12>,>11>,>13>,>5>,>6>]>>N>=>len>(arr)>># Function Call>>insertionSort(arr, N)>>printArray(arr, N)>>># This code is contributed by bgangwar59.>>>C#
// C# program for the above approach>using>System;>class>GFG>{>>// Function to sort an array using>>// insertion sort>>static>void>insertionSort(>int>[] arr,>int>n)>>{>>int>i, key, j;>>for>(i = 1; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> clé) { arr[j + 1] = arr[j]; j = j - 1 ; } arr[j + 1] = clé ; } } // Fonction pour imprimer un tableau de taille N static void printArray(int[] arr, int n) { int i; // Imprime le tableau pour (i = 0; i { Console.Write(arr[i] + ' '); } Console.WriteLine(); } // Code du pilote static public void Main() { int[] arr = new int[] { 12, 11, 13, 5, 6 }; int N = arr.Length; // Appel de fonction insertionSort(arr, N); printArray(arr, N); contribué par Dharanendra LV>>>Javascript
>// JavaScript program for the above approach>// Function to sort an array using>// insertion sort>function>insertionSort(arr,n)>{>>let i, key, j;>>for>(i = 1; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> clé) { arr[j + 1] = arr[j]; j = j - 1 ; } arr[j + 1] = clé ; } } // Fonction pour imprimer un tableau de taille N function printArray(arr,n) { let i; // Imprime le tableau pour (i = 0; i document.write(arr[i] + ' '); } document.write(' '); } // Code du pilote let arr=[12, 11 , 13, 5, 6]; let N = arr.length; // Appel de fonction insertionSort(arr, N); printArray(arr, N); // Ce code est fourni par avanitrachhadiya2155>>>Sortir:5 6 11 12 13>Le tri par sélection L'algorithme trie un tableau en recherchant à plusieurs reprises l'élément minimum (en tenant compte de l'ordre croissant) de la partie non triée et en le plaçant au début. L'algorithme maintient deux sous-tableaux dans un tableau donné.
- Le sous-tableau est déjà trié.
- Le sous-tableau restant n’est pas trié.
À chaque itération du tri par sélection, l'élément minimum (en tenant compte de l'ordre croissant) du sous-tableau non trié est sélectionné et déplacé vers le sous-tableau trié.
Vous trouverez ci-dessous un exemple pour expliquer les étapes ci-dessus :
arr[] = 64 25 12 22 11 // Find the minimum element in arr[0...4] // and place it at beginning 11 25 12 22 64 // Find the minimum element in arr[1...4] // and place it at beginning of arr[1...4] 11 12 25 22 64 // Find the minimum element in arr[2...4] // and place it at beginning of arr[2...4] 11 12 22 25 64 // Find the minimum element in arr[3...4] // and place it at beginning of arr[3...4] 11 12 22 25 64>Ci-dessous le programme correspondant :
C++
// C++ program for implementation of>// selection sort>#include>using>namespace>std;>// Function to swap two number>void>swap(>int>* xp,>int>* yp)>{>>int>temp = *xp;>>*xp = *yp;>>*yp = temp;>}>// Function to implement the selection>// sort>void>selectionSort(>int>arr[],>int>n)>{>>int>i, j, min_idx;>>// One by one move boundary of>>// unsorted subarray>>for>(i = 0; i // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element swap(&arr[min_idx], &arr[i]); } } // Function to print an array void printArray(int arr[], int size) { int i; for (i = 0; i cout << arr[i] << ' '; } cout << endl; } // Driver Code int main() { int arr[] = { 64, 25, 12, 22, 11 }; int n = sizeof(arr) / sizeof(arr[0]); // Function Call selectionSort(arr, n); cout << 'Sorted array: '; // Print the array printArray(arr, n); return 0; }>>>Java
// Java program for implementation of>// selection sort>import>java.util.*;>class>GFG>{>// Function to implement the selection>// sort>static>void>selectionSort(>int>arr[],>int>n)>{>>int>i, j, min_idx;>>// One by one move boundary of>>// unsorted subarray>>for>(i =>0>; i 1; i++) { // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element int temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array static void printArray(int arr[], int size) { int i; for (i = 0; i System.out.print(arr[i]+ ' '); } System.out.println(); } // Driver Code public static void main(String[] args) { int arr[] = { 64, 25, 12, 22, 11 }; int n = arr.length; // Function Call selectionSort(arr, n); System.out.print('Sorted array: '); // Print the array printArray(arr, n); } } // This code is contributed by aashish1995>>>Python3
# Python3 program for implementation of># selection sort># Function to implement the selection># sort>def>selectionSort(arr, n):>># One by one move boundary of>># unsorted subarray>>for>i>in>range>(n>->1>):>># Find the minimum element>># in unsorted array>>min_idx>=>i>>for>j>in>range>(i>+>1>, n):>>if>(arr[j] min_idx = j # Swap the found minimum element # with the first element arr[min_idx], arr[i] = arr[i], arr[min_idx] # Function to print an array def printArray(arr, size): for i in range(size): print(arr[i], end = ' ') print() # Driver Code if __name__ == '__main__': arr = [64, 25, 12, 22, 11] n = len(arr) # Function Call selectionSort(arr, n) print('Sorted array: ') # Print the array printArray(arr, n) # This code is contributed by ukasp>>>C#
couche réseau dans les réseaux informatiques
// C# program for implementation of>// selection sort>using>System;>public>class>GFG>{>// Function to implement the selection>// sort>static>void>selectionSort(>int>[]arr,>int>n)>{>>int>i, j, min_idx;>>// One by one move boundary of>>// unsorted subarray>>for>(i = 0; i { // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element int temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array static void printArray(int []arr, int size) { int i; for (i = 0; i Console.Write(arr[i]+ ' '); } Console.WriteLine(); } // Driver Code public static void Main(String[] args) { int []arr = { 64, 25, 12, 22, 11 }; int n = arr.Length; // Function Call selectionSort(arr, n); Console.Write('Sorted array: '); // Print the array printArray(arr, n); } } // This code is contributed by gauravrajput1>>>Javascript
>// Javascript program for implementation of>// selection sort>// Function to implement the selection>// sort>function>selectionSort(arr, n)>{>>let i, j, min_idx;>>>// One by one move boundary of>>// unsorted subarray>>for>(i = 0; i { // Find the minimum element // in unsorted array min_idx = i; for(j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element let temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array function printArray(arr, size) { let i; for(i = 0; i { document.write(arr[i] + ' '); } document.write(' '); } // Driver Code let arr = [ 64, 25, 12, 22, 11 ]; let n = arr.length; // Function Call selectionSort(arr, n); document.write('Sorted array: '); // Print the array printArray(arr, n); // This code is contributed by rag2127>>>Sortir:Sorted array: 11 12 22 25 64>Différence tabulaire entre le tri par insertion et le tri par sélection :
Tri par insertion Tri de sélection 1. Insère la valeur dans le tableau pré-trié pour trier l'ensemble des valeurs du tableau. Recherche le nombre minimum/maximum dans la liste et le trie par ordre croissant/décroissant. 2. C'est un algorithme de tri stable. C'est un algorithme de tri instable. 3. La complexité temporelle dans le meilleur des cas est Ω(N) lorsque le tableau est déjà en ordre croissant. Il a Θ(N2) dans le pire des cas et dans le cas moyen. Pour le meilleur des cas, le pire des cas et le tri de sélection moyen ont une complexité Θ(N2). 4. Le nombre d'opérations de comparaison effectuées dans cet algorithme de tri est inférieur au nombre d'échanges effectués. Le nombre d'opérations de comparaison effectuées dans cet algorithme de tri est supérieur au nombre d'échanges effectués. 5. Il est plus efficace que le tri Sélection. Il est moins efficace que le tri par insertion. 6. Ici les éléments sont connus à l'avance, et on recherche la bonne position pour les placer. L'emplacement où placer l'élément est préalablement connu, nous recherchons l'élément à insérer à cette position. 7. Le tri par insertion est utilisé lorsque :
- Le tableau comporte un petit nombre d’éléments
- Il ne reste plus que quelques éléments à trier
Le tri par sélection est utilisé lorsque
- Une petite liste est à trier
- Le coût de l'échange n'a pas d'importance
- La vérification de tous les éléments est obligatoire
- Le coût d'écriture dans la mémoire est important comme dans la mémoire flash (le nombre de swaps est de O(n) par rapport à O(n2) du tri à bulles)
8. Le tri par insertion est adaptatif, c'est-à-dire efficace pour les ensembles de données déjà substantiellement triés : la complexité temporelle est O (kn) lorsque chaque élément de l'entrée ne dépasse pas k endroits éloignés de sa position triée Le tri par sélection est un algorithme de tri par comparaison sur place
