- DFA fait référence à des automates finis déterministes. Déterministe fait référence au caractère unique du calcul. Les automates finis sont appelés automates finis déterministes si la machine lit une chaîne d'entrée un symbole à la fois.
- Dans DFA, il n'existe qu'un seul chemin pour les entrées spécifiques, de l'état actuel à l'état suivant.
- DFA n'accepte pas le déplacement nul, c'est-à-dire que DFA ne peut pas changer d'état sans aucun caractère d'entrée.
- DFA peut contenir plusieurs états finaux. Il est utilisé dans l'analyse lexicale du compilateur.
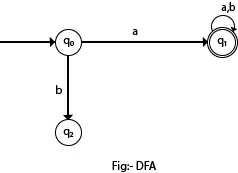
Dans le diagramme suivant, nous pouvons voir qu’à partir de l’état q0 pour l’entrée a, il n’y a qu’un seul chemin qui va vers q1. De même, à partir de q0, il n’existe qu’un seul chemin pour l’entrée b allant vers q2.
Définition formelle de DFA
Un DFA est une collection de 5 tuples identiques à ceux décrits dans la définition de FA.
Q: finite set of states ∑: finite set of the input symbol q0: initial state F: final state δ: Transition function
La fonction de transition peut être définie comme :
δ: Q x ∑→Q
Représentation graphique de DFA
Un DFA peut être représenté par des digraphes appelés diagramme d'état. Dans lequel:
- L'état est représenté par des sommets.
- L'arc étiqueté avec un caractère d'entrée montre les transitions.
- L'état initial est marqué par une flèche.
- L'état final est désigné par un double cercle.
Exemple 1:
Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q2} Solution:
Diagramme de transition :

Tableau de transition :
| État actuel | État suivant pour l'entrée 0 | État suivant de l'entrée 1 |
|---|---|---|
| →q0 | q0 | q1 |
| q1 | q2 | q1 |
| *q2 | q2 | q2 |
Exemple 2 :
DFA avec ∑ = {0, 1} accepte tout commençant par 0.
sélectionner plusieurs tables SQL
Solution:

Explication:
- Dans le diagramme ci-dessus, nous pouvons voir que si 0 est donné comme entrée du DFA dans l'état q0, le DFA change d'état en q1 et passe toujours à l'état final q1 au démarrage de l'entrée 0. Il peut accepter 00, 01, 000, 001... .etc. Il ne peut accepter aucune chaîne commençant par 1, car il n'atteindra jamais l'état final sur une chaîne commençant par 1.
Exemple 3 :
DFA avec ∑ = {0, 1} accepte tous les éléments se terminant par 0.
Solution:

Explication:
Dans le diagramme ci-dessus, nous pouvons voir que si 0 est donné en entrée du DFA dans l'état q0, le DFA change d'état en q1. Il peut accepter n'importe quelle chaîne se terminant par 0 comme 00, 10, 110, 100....etc. Il ne peut accepter aucune chaîne se terminant par 1, car il n'ira jamais à l'état final q1 sur 1 entrée, donc la chaîne se terminant par 1 ne sera pas acceptée ou sera rejetée.
