L'intérêt composé est l'intérêt calculé sur le montant d'un prêt ou d'un dépôt dans lequel les intérêts sont calculés pour le principal ainsi que les intérêts gagnés précédemment.

La différence commune entre les intérêts composés et simples est que dans intérêts composés , les intérêts sont calculés sur le montant principal ainsi que sur les intérêts précédemment gagnés alors que les intérêts simples dépendent uniquement du principal investi.

Table des matières

• Qu’est-ce que l’intérêt composé ?
• Formule d'intérêt composé
• Comment calculer les intérêts composés ?
• Formule d’intérêt composé – Dérivation
• Formule d'intérêt composé semestrielle
• Formule d'intérêt composé trimestriel
• Formule d'intérêt composé mensuel
• Formule d'intérêt composé quotidien
• Formule du taux de composition périodique
• Règle de 72
• Intérêts composés d’années consécutives
• Formule d’intérêt composé continu
• Quelques autres applications des intérêts composés
• Différence entre les intérêts composés et les intérêts simples
• Exemples d'intérêts composés
• Intérêt composé – Questions pratiques

Qu’est-ce que l’intérêt composé ?

Les intérêts composés sont les intérêts sur le montant principal ainsi que les intérêts gagnés sur le montant principal. Le mot intérêt composé est composé de deux mots Composé signifie composé de deux ou plus et Intérêt signifie l'argent gagné en prêtant le montant. Par conséquent, les intérêts composés sont l’argent gagné sur les prêts et ils sont composés de deux types d’intérêts qui sont :

• Intérêts sur le capital

• Intérêts sur les intérêts gagnés sur le capital au cours de la période

Définition des intérêts composés

Intérêts composés est l'intérêt calculé sur le capital et les intérêts gagnés précédemment. Il est désigné par C.I. Il est très utile à des fins d’investissement et de remboursement de prêts. On l’appelle également intérêt sur intérêt.

comment centrer une image sur CSS

Intérêts composés est très utile dans les secteurs bancaire et financier et est également utile dans d’autres secteurs. Quelques-unes de ses utilisations sont :

• Croissance de la population d'un pays
• Valeur de l'investissement sur une période donnée.
• Pour trouver les coûts gonflés et la valeur dépréciée de tout article.
• Pour prédire la croissance de n’importe quelle institution ou pays.

Intérêts composés (C.I) = Montant – Principal

Formule d'intérêt composé

Intérêts composés est calculé, après avoir calculé le montant total sur une période de temps, en fonction du taux d'intérêt et du principal initial. Pour un principal initial de P, un taux d'intérêt annuel de r, une période de temps t en années, une fréquence du nombre de fois où les intérêts sont composés annuellement n, la formule de calcul de CI est la suivante :

IC = P(1 + r/100) ⁿ –P

La formule ci-dessus pour calculer les intérêts composés est ajoutée sous la forme d'image ci-dessous :

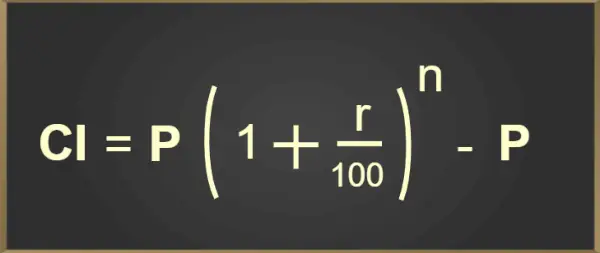
Formule d'intérêt composé

Où,

• P = Principal
• r = Taux d'intérêt
• n = Nombre de fois où les intérêts sont composés par an
• t = Temps (en années)

Nous pouvons écrire la formule des intérêts composés comme suit :

Intérêts composés = A – P

Où,

• UN = Montant total d’argent après composition
• P = Montant du capital initial

Intérêts composés = P(1 + r/n) ^NT -P

Où,

• P = Montant du capital initial
• r = taux d'intérêt annuel
• n = Nombre de fois où les intérêts sont composés
• t = Nombre d'années

Les intérêts composés peuvent être calculés annuellement, semestriellement, trimestriellement, mensuellement, quotidiennement, etc. selon les besoins.

Comment calculer les intérêts composés ?

Intérêts composés représente les intérêts payés à la fois sur le principal et sur les intérêts accumulés. Les intérêts gagnés à chaque intervalle sont ajoutés au capital initial et le capital continue donc d'augmenter.

Utilisez les méthodes suivantes pour trouver les intérêts composés.

Étape 1: Note, principal, taux et période indiquée

Étape 2 : Calculez le montant en utilisant la formule A = P(1 + r/100) ⁿ

Étape 3 : Recherchez les intérêts composés à l'aide de la formule CI = Montant – Capital

À intervalles réguliers, les intérêts accumulés jusqu'à présent sont ajoutés au montant principal existant, puis les intérêts sont calculé pour le nouveau principal . Le nouveau capital est égal à la somme du capital initial et des intérêts accumulés jusqu'à présent.

Intérêts composés = Intérêts sur le capital + Intérêts sur les intérêts du principal (à partir de la deuxième année)

Les intérêts composés sont calculés à intervalles réguliers, par exemple annuellement, semestriellement, trimestriellement, mensuellement, etc; C’est comme si réinvestir les revenus d’intérêts d’un investissement permettait à l’argent de croître plus rapidement au fil du temps ! C’est exactement ce que les intérêts composés font à l’argent. Les banques ou tout organisme financier calculent le montant uniquement sur la base des intérêts composés.

Formule d’intérêt composé – Dérivation

La formule des intérêts composés est un outil puissant utilisé en finance pour calculer les intérêts gagnés ou payés sur un montant principal initial, qui comprend à la fois le principal initial et les intérêts accumulés au cours des périodes précédentes. La formule des intérêts composés est donnée par :

Où,

• A représente la valeur future de l'investissement ou du prêt, intérêts compris
• P est le montant principal (investissement initial ou montant du prêt)
• r est le taux d'intérêt annuel (sous forme décimale)
• n est le nombre de fois où les intérêts sont composés par an
• c'est le temps pendant lequel l'argent est investi ou emprunté, en années

Formule d'intérêt simple

Les intérêts simples sont calculés uniquement sur le montant principal. Il peut être représenté par la formule ,

Formule d'intérêt composé avec composition continue

Lorsque les intérêts sont composés en continu (une infinité de fois par an), la formule des intérêts composés est dérivée de la formule de composition continue :

Où,

• e est le nombre d'Euler (environ 2,71828)
• P est le capital
• r est le taux d'intérêt annuel
• c'est le temps en années

Formule générale des intérêts composés

Pour dériver la formule générale des intérêts composés, considérons les intérêts composés n fois par an.

Si P est composé n fois par an à un taux d'intérêt annuel r, l'intérêt r est divisé par n et appliqué n fois par an. Ainsi, après t années, la formule devient :

Où,

• représente le taux d’intérêt par période de composition.
• nt est le nombre total de périodes de composition sur t années.

Ce la formule illustre comment le montant du capital initial augmente au fil du temps lorsque les intérêts sont composés à intervalles réguliers . À mesure que n tend vers l'infini (c'est-à-dire la composition continue), la formule converge vers la formule de composition continue .

En résumé, la formule des intérêts composés est le résultat de la formule de composition continue adaptée à des périodes de composition distinctes par an. Il permet de calculer la valeur future d'un investissement ou d'un prêt, en tenant compte des intérêts composés à intervalles réguliers.

Formule d'intérêt composé semestrielle

Supposons que le principal investi soit P et le taux d'intérêt soit R % par an, composé semestriellement pendant « t » années.

Comme il est composé semestriellement, le capital sera modifié au bout de 6 mois, et les intérêts gagnés jusque-là seront ajoutés au principal et celui-ci deviendra alors le nouveau principal. De même, le montant final est calculé.

Nous savons,

taux = R% par an composé semestriel

taux = (R/2) %

le temps est de t années, nous savons que t années ont 2t demi-années.

Maintenant,

A = P (1 + R/200) ^2t

IC = A – P

Formule d'intérêt composé trimestriel

Supposons que le principal investi soit P et que le taux d'intérêt soit R % par an, composé trimestriellement pendant t ans.

Comme il est composé trimestriellement, le capital sera modifié au bout de 3 mois, et les intérêts gagnés jusque-là seront ajoutés au principal et celui-ci deviendra alors le nouveau principal. De même, le montant final est calculé.

nous savons,

taux = R% par an composé trimestriellement

taux = (R/4)%

le temps est de t années, nous savons que t années ont 4t quarts.

Maintenant,

UNE = P(1 + R/400) ^4t

IC = A – P

Vérifier: Formule d'intérêt composé trimestriel

Formule d'intérêt composé mensuel

Si les intérêts sont composés mensuellement, le nombre de fois où ils seront composés sera de 12 et les intérêts chaque mois seront 1/12 des intérêts composés annuels. Par conséquent, la formule d’intérêt composé mensuel est donnée comme suit :

UNE = P[1 + (R/1200)] ^12t

IC = A – P

clé du candidat

Vérifier: Formule d'intérêt composé mensuel

Formule d'intérêt composé quotidien

Si les intérêts sont composés quotidiennement, alors.

Le nouveau taux d'intérêt sera de R/365 %

n = 365

Par conséquent, la formule d’intérêt composé quotidien est donnée comme suit :

UNE = P[1 + (R/36500)] ^365t

IC = A – P

Formule du taux de composition périodique

Le montant total, incluant le principal P et les intérêts composés CI, est donné par :

UNE = P[1 + (r/n)] ^NT

où,

• P = Principal
• A = Montant final
• r = taux d'intérêt annuel
• n = Nombre de fois où les intérêts sont composés
• t = Temps (en années)

Ainsi, les intérêts composés sont :

IC = A – P

Règle de 72

La règle de 72 est la formule utilisée pour estimer combien d’années notre argent est doublé s’il est composé annuellement. Pour exemple , si notre argent est investi à r % composé annuellement, il faut 72/r ans pour que notre argent double.

Ce calcul est également utile pour calculer la valeur gonflée de notre argent, c'est-à-dire qu'il indique au bout de combien d'années la valeur de notre actif est réduite de moitié s'il est amorti annuellement.

Formule de la règle de 72

La formule suivante est utilisée pour approximer le nombre d’années pendant lesquelles notre investissement sera doublé.

N = 72 /r

où,

• N est le nombre approximatif d'années où notre argent est doublé
• r est le taux auquel notre argent est composé annuellement

Exemple de règle de 72

Supposons que Kabir ait investi 10 000 000 roupies dans un fonds de dette qui donne un rendement de 8 %. Trouvez au bout de combien d’années son argent est doublé s’il est composé annuellement.

En utilisant la formule ci-dessus : N = 72/8 = 9 ans

Ainsi, il faut 9 ans pour que l’argent de Kabir soit doublé.

Intérêts composés d’années consécutives

Si nous avons la même somme et le même taux d’intérêt. Le ci. d'une année particulière est toujours supérieur au C.I de l'année précédente. (L'IC de la 3ème année est supérieur à l'IC de la 2ème année). La différence entre les CI pour deux années consécutives correspond aux intérêts d'un an sur les CI de l'année précédente.

C.I de 3ème année – C.I de 2ème année = C.I de 2ème année × r × 1/100

La différence entre les montants de deux années consécutives correspond aux intérêts d’une année sur le montant de l’année précédente.

Montant de 3ème année – Montant de 2ème année = Montant de 2ème année × r × 1/100

Résultats clés

Quand on a la même somme et le même tarif ,

bash concaténer des chaînes

C.I pour la nième année = C.I pour la (n – 1)ième année + Intérêts pour un an sur C.I pour la (n – 1)ième année

Formule d’intérêt composé continu

La formule de composition continue est utilisée en finance pour calculer la valeur finale d'un investissement qui subit une composition continue sur différentes périodes et la valeur est ajoutée au fil du temps. La formule de composition continue est donnée par

Valeur finale = Valeur actuelle × e ^rt

où,

• r est le taux d'intérêt
• il est temps

Apprendre encore plus, Formule de composition continue

Quelques autres applications des intérêts composés

Croissance: Ceci est principalement utilisé pour la croissance si les industries sont liées.

Production après n ans = production initiale × (1 + r/100) ⁿ

Dépréciation : Lorsque le coût d'un produit se déprécie de r% chaque année, alors sa valeur après n ans est

Valeur actuelle × (1 + r/100) ⁿ

Problèmes de population : lorsque la population d'une ville ou d'un village augmente à un certain rythme par an.

Population après n années = population actuelle × (1 + r/100) ⁿ

Différence entre les intérêts composés et les intérêts simples

La différence entre les intérêts composés et les intérêts simples peut être apprise ci-dessous dans cet article.

Exemples d'intérêts composés

Voici quelques exemples de formules d’intérêts composés :

Exemple 1 : Trouvez l'intérêt composé lorsque le principal = Rs 6 000, le taux = 10 % par an et la durée = 2 ans.

Solution:

Intérêts pour la première année = (6 000 × 10 × 1)/100 = 600

Montant à la fin de la première année = 6000 + 600 = 6600

Intérêts pour la deuxième année = (6600 × 10 × 1) / 100 = 660

Montant en fin de deuxième année = 6600 + 660 = 7260

Intérêts composés = 7 260 – 6 000 = 1 260

Exemple 2 : Quel sera l'intérêt composé sur Rs 8000 dans deux ans lorsque le taux d'intérêt est de 2 % par an ?

Solution:

Donné,

• P principal = 8000
• Taux r = 2%
• Temps = 2 ans

par formule

A = P (1 + R/100) ⁿ

A = 8 000 (1 + 2/100)²= 8000 (102/100)²

A = 8323

Intérêts composés = A – P = 8323 – 8000 = Rs 323

Exemple 3 : Hari a déposé Rs. 4000 auprès d'une société de financement pendant 2 ans à un intérêt de 5% par an. Quels sont les intérêts composés que Rohit reçoit après 2 ans ?

Solution:

Donné,

• P principal = 4000
• Taux r = 5%
• Temps = 2 ans

Par formule,

A = P (1 + R/100)ⁿ

UNE= 4000 (1 + 5/100)²

A= 4000 (105/100)²

A= 4410

Intérêts composés = A – P = 4410 – 4000 = 410

Exemple 4 : Trouvez les intérêts composés sur Rs. 2000 au taux de 4 % par an pendant 1,5 an. Quand les intérêts sont composés semestriellement ?

Solution:

Donné,

• Principal p = 2000
• Taux r = 4%
• Temps = 1,5 (soit 3 demi-années)

par formule,

A = P (1 + R/200) ²ⁿ

A = 2000 (1 + 4/200) ³

A = 2000 (204/200) ³

comment imprimer Java

A = 2122

Intérêts composés = A – P = 2122 – 2000 = 122

Exemple 5 : Quel est l'intérêt composé sur 10 000 pendant un an au taux de 20 % par an, si l'intérêt est composé trimestriellement ?

Solution:

Donné,

• Principal P = Rs 10000
• Taux R = 12% (12/4 = 3 % par trimestre)
• Temps = 1 an (1 × 4 = 4 trimestres)

Par formule,

A = P (1 + R/100) ⁿ

A = 10 000 (1 + 3/100) ⁴

A = 10 000 (103/100) ⁴

A = 11255

Intérêts composés = A – P = 11255 – 10000 = 1255

Exemple 6 : Trouvez les intérêts composés au taux de 5 % par an pendant 2 ans sur ce principal qui, dans 2 ans, au taux de 5 % par an étant donné Rs. 400 comme intérêts simples.

Solution:

Donné,

• Intérêt simple SI = 400
• Taux R = 5%
• Temps T = 2 ans

Par formule,

Intérêt simple = (P × T × R)/100

⇒ P = (SI × 100)/T × R

P = (400 × 100)/2 × 5 Taux d'intérêt composé = 5 %

P = 40 000/10 = Rs 4 000

Temps = 2 ans

Par formule,

A = P (1 + R/100)

A = 4000 (1 + 5/100)

A = 4410

Intérêts composés = A – P = 4410 – 4000 = 410

Exemple 7 : Trouvez les intérêts composés sur Rs 30 000 à 7 % d'intérêt composé annuellement pendant deux ans.

Solution:

• Principal P = Rs 30000
• Taux R = 7%
• Durée = 2 ans

Par formule,

A = P (1 + R/100) ⁿ

A = 30 000 (1 + 7/100) ²

A = 30 000 (107/100) ²

bool pour chaîner java

A = 34347

Intérêts composés = A – P = 34347 – 30000 = 4347

Lectures connexes :

• Intérêts composés quotidiens
• Intérêts composés mensuels
• Solution d’intérêt composé de classe 8
• Intérêts composés – Questions et réponses sur les aptitudes
• Intérêt simple

Intérêt composé – Questions pratiques

Diverses questions pratiques sur les intérêts composés sont,

T1. Trouvez le montant qui doit être payé après 3 ans si une somme de 10 000 est prêtée au taux de 4 % composé annuellement.

Q2. Trouvez les intérêts qui doivent être payés après 1,5 an si une somme de 2 500 est prêtée au taux de 6 % composé semestriellement.

Q3. Calculez les intérêts composés pour un montant de 9000 prêtés au taux de 5% trimestriellement pendant 15 mois.

Q4. Calculer les intérêts composés pour un montant de 20000 prêtés au taux de 12% pendant 3 mois composés mensuellement

Conclusion des intérêts composés

Les intérêts composés sont un concept financier puissant qui permet aux investissements ou aux prêts de croître ou de s’accumuler au fil du temps. Contrairement à les intérêts simples, qui calculent uniquement les intérêts sur le montant initial du principal, intérêts composés prend en compte les intérêts gagnés à la fois sur le principal initial et sur les intérêts accumulés des périodes précédentes.

Intérêts composés – FAQ

Que signifient les intérêts composés ?

Les intérêts composés sont les intérêts calculés sur le capital ainsi que les intérêts antérieurs gagnés sur une période de temps déterminée.

Comment calculer les intérêts composés ?

Pour calculer les intérêts composés, le montant final est d’abord calculé, puis il est soustrait du principal pour obtenir l’intérêt composé final. Le montant est calculé selon la formule,

UNE = P(1 + R/100) ^t

IC = A – P

L’intérêt composé est-il meilleur que l’intérêt simple pour les investisseurs ?

Oui, les intérêts composés sont bien meilleurs que les intérêts simples pour les investisseurs.

Qu’est-ce que la formule d’intérêt composé si elle est composée quotidiennement ?

Supposons que le principal donné soit P, le taux soit R et l'intervalle de temps soit de T années, alors la formule des intérêts composés lorsqu'ils sont composés quotidiennement est :

UNE = P(1 + R/365) ^{{365 × T}}

Quelle est la différence entre CI et SI ?

La différence fondamentale entre CI et SI est que SI correspond aux intérêts facturés sur le capital, tandis que CI correspond aux intérêts facturés sur le capital ainsi que sur les intérêts accumulés sur le capital.