
Compte tenu d'un graphe non orienté connecté représenté par une liste de contiguïté adjListe[][] avec n nœuds et m arêtes avec chaque nœud ayant un étiquette distincte depuis 0 à n-1 et chaque adj[i] représente la liste des sommets connectés au sommet i.
Créer un cloner du graphique où chaque nœud du graphique contient un entier Val et un tableau ( voisins ) de nœuds contenant des nœuds adjacents au nœud actuel.
Nœud de classe {
val : entier
voisins : Liste[Nœud]
}Java obtient la date actuelle
Votre tâche consiste à cloner le graphique donné et à renvoyer une référence au graphique cloné.
Note: Si vous renvoyez une copie correcte du graphique donné, la sortie sera vraie ; sinon, si la copie est incorrecte, elle s'imprimera faussement.
Exemples
java math.min
Saisir: n = 4 adjList[][] = [[1 2] [0 2] [0 1 3] [2]]
Sortir: vrai
Explication:
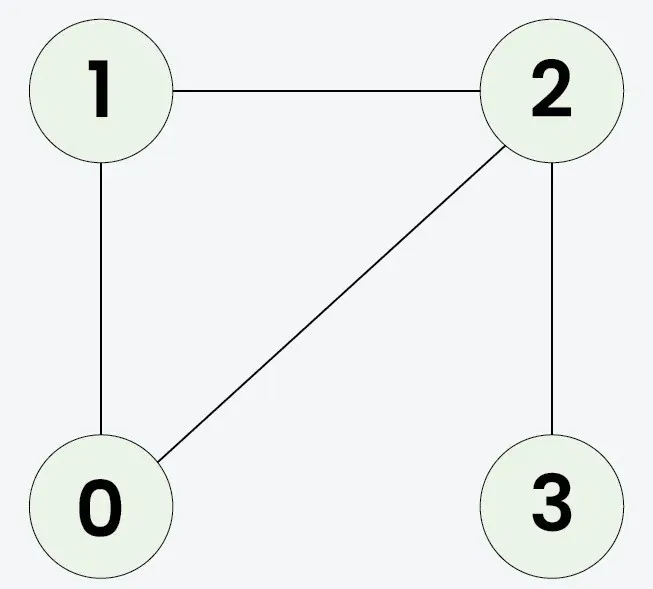
Puisque le graphique cloné est identique à l’original, la sortie sera vraie.Saisir: n = 3 adjList[][] = [[1 2] [0] [0]]
Sortir: vrai
Explication:
Puisque le graphique cloné est identique à l’original, la sortie sera vraie.
Table des matières
- Pourquoi devons-nous suivre les nœuds visités/clonés ?
- Comment garder une trace des nœuds visités/clonés ?
- Comment connecter des nœuds clones ?
- Comment vérifier si le graphique cloné est correct ?
- [Approche 1] Utilisation du parcours BFS - O(V+E) Time et O(V) Space
- [Approche 2] Utilisation du parcours DFS - O(V+E) Time et O(V) Space
Pourquoi devons-nous suivre les nœuds visités/clonés ?
Nous devons suivre les nœuds visités ou clonés pour éviter une récursion infinie et un travail redondant lors du clonage d'un graphique. Étant donné que les graphiques peuvent contenir des cycles (dans lesquels un nœud peut pointer vers un nœud précédemment visité) sans garder la trace des nœuds que nous avons déjà clonés, la fonction de clonage revisiterait sans cesse les mêmes nœuds, ce qui entraînerait un débordement de pile ou une duplication incorrecte.
Comment garder une trace des nœuds visités/clonés ?
Un HashMap/Map est requis afin de conserver tous les nœuds déjà créés. Magasins de clés : Référence/Adresse du nœud d'origine Magasins de valeur : Référence/Adresse du nœud cloné Une copie de tous les nœuds du graphe a été réalisée.
Comment connecter des nœuds clones ?
En visitant les sommets voisins d'un nœud dans obtenir le cloné correspondant nœud pour toi, appelons ça DANS visitez maintenant tous les nœuds voisins pour dans et pour chaque voisin, trouvez le nœud clone correspondant (s'il n'est pas trouvé, créez-en un), puis poussez-le dans le vecteur voisin de DANS nœud.
Comment vérifier si le graphique cloné est correct ?
Effectuez un parcours BFS sur le graphique d'origine avant le clonage, puis à nouveau sur le graphique cloné une fois le clonage terminé. Lors de chaque parcours, imprimez la valeur de chaque nœud ainsi que son adresse (ou référence). Pour vérifier l'exactitude du clonage, comparez l'ordre des nœuds visités dans les deux parcours. Si les valeurs des nœuds apparaissent dans le même ordre mais que leurs adresses (ou références) diffèrent, cela confirme que le graphique a été cloné avec succès et correctement.
Découvrez comment cloner un graphe non orienté comprenant des graphiques avec plusieurs composants connectés en utilisant BFS ou DFS pour garantir une copie complète et complète de tous les nœuds et bords.
[Approche 1] Utilisation du parcours BFS - O(V+E) Time et O(V) Space
C++Dans l'approche BFS, le graphe est cloné de manière itérative à l'aide d'une file d'attente. Nous commençons par cloner le nœud initial et le plaçant dans la file d'attente. Au fur et à mesure que nous traitons chaque nœud de la file d'attente, nous visitons ses voisins. Si un voisin n'a pas encore été cloné, nous créons un clone, le stockons dans une carte et le mettons en file d'attente pour un traitement ultérieur. Nous ajoutons ensuite le clone du voisin à la liste des voisins du clone du nœud actuel. Ce processus se poursuit niveau par niveau, garantissant que tous les nœuds sont visités dans l'ordre de la largeur. BFS est particulièrement utile pour éviter une récursion profonde et gérer efficacement des graphiques volumineux ou larges.
java obtient l'heure actuelle
#include
import java.util.*; // Definition for a Node class Node { public int val; public ArrayList<Node> neighbors; public Node() { neighbors = new ArrayList<>(); } public Node(int val) { this.val = val; neighbors = new ArrayList<>(); } } public class GfG { // Clone the graph public static Node cloneGraph(Node node) { if (node == null) return null; Map<Node Node> mp = new HashMap<>(); Queue<Node> q = new LinkedList<>(); // Clone the starting node Node clone = new Node(node.val); mp.put(node clone); q.offer(node); while (!q.isEmpty()) { Node current = q.poll(); for (Node neighbor : current.neighbors) { // Clone neighbor if it hasn't been cloned yet if (!mp.containsKey(neighbor)) { mp.put(neighbor new Node(neighbor.val)); q.offer(neighbor); } // Add the clone of the neighbor to the current node's clone mp.get(current).neighbors.add(mp.get(neighbor)); } } return mp.get(node); } // Build graph public static Node buildGraph() { Node node1 = new Node(0); Node node2 = new Node(1); Node node3 = new Node(2); Node node4 = new Node(3); node1.neighbors.addAll(new ArrayList<> (Arrays.asList(node2 node3))); node2.neighbors.addAll(new ArrayList<> (Arrays.asList(node1 node3))); node3.neighbors.addAll(new ArrayList<> (Arrays.asList(node1 node2 node4))); node4.neighbors.addAll(new ArrayList<> (Arrays.asList(node3))); return node1; } // Compare two graphs for structure and value public static boolean compareGraphs(Node n1 Node n2 HashMap<Node Node> visited) { if (n1 == null || n2 == null) return n1 == n2; if (n1.val != n2.val || n1 == n2) return false; visited.put(n1 n2); if (n1.neighbors.size() != n2.neighbors.size()) return false; for (int i = 0; i < n1.neighbors.size(); i++) { Node neighbor1 = n1.neighbors.get(i); Node neighbor2 = n2.neighbors.get(i); if (visited.containsKey(neighbor1)) { if (visited.get(neighbor1) != neighbor2) return false; } else { if (!compareGraphs(neighbor1 neighbor2 visited)) return false; } } return true; } public static void main(String[] args) { Node original = buildGraph(); Node cloned = cloneGraph(original); boolean isEqual = compareGraphs(original cloned new HashMap<>()); System.out.println(isEqual ? 'true' : 'false'); } }
from collections import deque # Definition for a Node class Node: def __init__(self val=0): self.val = val self.neighbors = [] # Clone the graph def cloneGraph(node): if not node: return None # Map to hold original nodes as keys and their clones as values mp = {} # Initialize BFS queue q = deque([node]) # Clone the starting node mp[node] = Node(node.val) while q: current = q.popleft() for neighbor in current.neighbors: # If neighbor not cloned yet if neighbor not in mp: mp[neighbor] = Node(neighbor.val) q.append(neighbor) # Link clone of neighbor to the clone of the current node mp[current].neighbors.append(mp[neighbor]) return mp[node] # Build graph def buildGraph(): node1 = Node(0) node2 = Node(1) node3 = Node(2) node4 = Node(3) node1.neighbors = [node2 node3] node2.neighbors = [node1 node3] node3.neighbors = [node1 node2 node4] node4.neighbors = [node3] return node1 # Compare two graphs structurally and by values def compareGraphs(n1 n2 visited): if not n1 or not n2: return n1 == n2 if n1.val != n2.val or n1 is n2: return False visited[n1] = n2 if len(n1.neighbors) != len(n2.neighbors): return False for i in range(len(n1.neighbors)): neighbor1 = n1.neighbors[i] neighbor2 = n2.neighbors[i] if neighbor1 in visited: if visited[neighbor1] != neighbor2: return False else: if not compareGraphs(neighbor1 neighbor2 visited): return False return True # Driver if __name__ == '__main__': original = buildGraph() cloned = cloneGraph(original) result = compareGraphs(original cloned {}) print('true' if result else 'false')
using System; using System.Collections.Generic; // Definition for a Node public class Node { public int val; public List<Node> neighbors; public Node() { neighbors = new List<Node>(); } public Node(int val) { this.val = val; neighbors = new List<Node>(); } } class GfG { // Clone the graph public static Node CloneGraph(Node node) { if (node == null) return null; var mp = new Dictionary<Node Node>(); var q = new Queue<Node>(); // Clone the starting node var clone = new Node(node.val); mp[node] = clone; q.Enqueue(node); while (q.Count > 0) { var current = q.Dequeue(); foreach (var neighbor in current.neighbors) { // If neighbor not cloned clone it and enqueue if (!mp.ContainsKey(neighbor)) { mp[neighbor] = new Node(neighbor.val); q.Enqueue(neighbor); } // Add clone of neighbor to clone of current mp[current].neighbors.Add(mp[neighbor]); } } return mp[node]; } // Build graph public static Node BuildGraph() { var node1 = new Node(0); var node2 = new Node(1); var node3 = new Node(2); var node4 = new Node(3); node1.neighbors.AddRange(new[] { node2 node3 }); node2.neighbors.AddRange(new[] { node1 node3 }); node3.neighbors.AddRange(new[] { node1 node2 node4 }); node4.neighbors.AddRange(new[] { node3 }); return node1; } // Compare two graphs for structure and value public static bool CompareGraphs(Node n1 Node n2 Dictionary<Node Node> visited) { if (n1 == null || n2 == null) return n1 == n2; if (n1.val != n2.val || ReferenceEquals(n1 n2)) return false; visited[n1] = n2; if (n1.neighbors.Count != n2.neighbors.Count) return false; for (int i = 0; i < n1.neighbors.Count; i++) { var neighbor1 = n1.neighbors[i]; var neighbor2 = n2.neighbors[i]; if (visited.ContainsKey(neighbor1)) { if (!ReferenceEquals(visited[neighbor1] neighbor2)) return false; } else { if (!CompareGraphs(neighbor1 neighbor2 visited)) return false; } } return true; } public static void Main() { var original = BuildGraph(); var cloned = CloneGraph(original); var visited = new Dictionary<Node Node>(); Console.WriteLine(CompareGraphs(original cloned visited) ? 'true' : 'false'); } }
// Definition for a Node class Node { constructor(val = 0) { this.val = val; this.neighbors = []; } } // Clone the graph function cloneGraph(node) { if (!node) return null; const mp = new Map(); const q = [node]; // Clone the initial node mp.set(node new Node(node.val)); while (q.length > 0) { const current = q.shift(); for (const neighbor of current.neighbors) { if (!mp.has(neighbor)) { mp.set(neighbor new Node(neighbor.val)); q.push(neighbor); } // Link clone of neighbor to clone of current mp.get(current).neighbors.push(mp.get(neighbor)); } } return mp.get(node); } // Build graph function buildGraph() { const node1 = new Node(0); const node2 = new Node(1); const node3 = new Node(2); const node4 = new Node(3); node1.neighbors = [node2 node3]; node2.neighbors = [node1 node3]; node3.neighbors = [node1 node2 node4]; node4.neighbors = [node3]; return node1; } // Compare two graphs structurally and by value function compareGraphs(n1 n2 visited = new Map()) { if (!n1 || !n2) return n1 === n2; if (n1.val !== n2.val || n1 === n2) return false; visited.set(n1 n2); if (n1.neighbors.length !== n2.neighbors.length) return false; for (let i = 0; i < n1.neighbors.length; i++) { const neighbor1 = n1.neighbors[i]; const neighbor2 = n2.neighbors[i]; if (visited.has(neighbor1)) { if (visited.get(neighbor1) !== neighbor2) return false; } else { if (!compareGraphs(neighbor1 neighbor2 visited)) return false; } } return true; } // Driver const original = buildGraph(); const cloned = cloneGraph(original); const result = compareGraphs(original cloned); console.log(result ? 'true' : 'false');
Sortir
true
[Approche 2] Utilisation du parcours DFS - O(V+E) Time et O(V) Space
C++Dans l'approche DFS, le graphique est cloné par récursivité. Nous partons du nœud donné et explorons autant que possible le long de chaque branche avant de revenir en arrière. Une carte (ou un dictionnaire) est utilisée pour garder une trace des nœuds déjà clonés afin d'éviter de traiter plusieurs fois le même nœud et de gérer les cycles. Lorsque nous rencontrons un nœud pour la première fois, nous en créons un clone et le stockons sur la carte. Ensuite, pour chaque voisin de ce nœud, nous le clonons de manière récursive et ajoutons le voisin cloné au clone du nœud actuel. Cela garantit que tous les nœuds sont visités en profondeur avant de revenir et que la structure du graphique est fidèlement copiée.
#include
import java.util.*; // Definition for a Node class Node { int val; ArrayList<Node> neighbors; Node() { neighbors = new ArrayList<>(); } Node(int val) { this.val = val; neighbors = new ArrayList<>(); } } public class GfG { // Map to hold original node to its copy static HashMap<Node Node> copies = new HashMap<>(); // Function to clone the graph using DFS public static Node cloneGraph(Node node) { // If the node is NULL return NULL if (node == null) return null; // If node is not yet cloned clone it if (!copies.containsKey(node)) { Node clone = new Node(node.val); copies.put(node clone); // Recursively clone neighbors for (Node neighbor : node.neighbors) { clone.neighbors.add(cloneGraph(neighbor)); } } // Return the clone return copies.get(node); } // Build graph public static Node buildGraph() { Node node1 = new Node(0); Node node2 = new Node(1); Node node3 = new Node(2); Node node4 = new Node(3); node1.neighbors.addAll(Arrays.asList(node2 node3)); node2.neighbors.addAll(Arrays.asList(node1 node3)); node3.neighbors.addAll(Arrays.asList(node1node2 node4)); node4.neighbors.addAll(Arrays.asList(node3)); return node1; } // Compare two graphs for structural and value equality public static boolean compareGraphs(Node node1 Node node2 HashMap<Node Node> visited) { if (node1 == null || node2 == null) return node1 == node2; if (node1.val != node2.val || node1 == node2) return false; visited.put(node1 node2); if (node1.neighbors.size() != node2.neighbors.size()) return false; for (int i = 0; i < node1.neighbors.size(); i++) { Node n1 = node1.neighbors.get(i); Node n2 = node2.neighbors.get(i); if (visited.containsKey(n1)) { if (visited.get(n1) != n2) return false; } else { if (!compareGraphs(n1 n2 visited)) return false; } } return true; } // Driver Code public static void main(String[] args) { Node original = buildGraph(); // Clone the graph Node cloned = cloneGraph(original); // Compare original and cloned graph boolean result = compareGraphs(original cloned new HashMap<>()); System.out.println(result ? 'true' : 'false'); } }
# Definition for a Node class Node: def __init__(self val=0 neighbors=None): self.val = val self.neighbors = neighbors if neighbors is not None else [] # Map to hold original node to its copy copies = {} # Function to clone the graph def cloneGraph(node): # If the node is None return None if not node: return None # If node is not yet cloned clone it if node not in copies: # Create a clone of the node clone = Node(node.val) copies[node] = clone # Recursively clone neighbors for neighbor in node.neighbors: clone.neighbors.append(cloneGraph(neighbor)) # Return the clone return copies[node] def buildGraph(): node1 = Node(0) node2 = Node(1) node3 = Node(2) node4 = Node(3) node1.neighbors = [node2 node3] node2.neighbors = [node1 node3] node3.neighbors = [node1 node2 node4] node4.neighbors = [node3] return node1 # Compare two graphs for structural and value equality def compareGraphs(node1 node2 visited): if not node1 or not node2: return node1 == node2 if node1.val != node2.val or node1 is node2: return False visited[node1] = node2 if len(node1.neighbors) != len(node2.neighbors): return False for i in range(len(node1.neighbors)): n1 = node1.neighbors[i] n2 = node2.neighbors[i] if n1 in visited: if visited[n1] != n2: return False else: if not compareGraphs(n1 n2 visited): return False return True # Driver Code if __name__ == '__main__': original = buildGraph() # Clone the graph using DFS cloned = cloneGraph(original) # Compare original and cloned graph visited = {} print('true' if compareGraphs(original cloned visited) else 'false')
using System; using System.Collections.Generic; public class Node { public int val; public List<Node> neighbors; public Node() { val = 0; neighbors = new List<Node>(); } public Node(int _val) { val = _val; neighbors = new List<Node>(); } } class GfG { // Dictionary to hold original node to its copy static Dictionary<Node Node> copies = new Dictionary<Node Node>(); // Function to clone the graph using DFS public static Node CloneGraph(Node node) { // If the node is NULL return NULL if (node == null) return null; // If node is not yet cloned clone it if (!copies.ContainsKey(node)) { Node clone = new Node(node.val); copies[node] = clone; // Recursively clone neighbors foreach (Node neighbor in node.neighbors) { clone.neighbors.Add(CloneGraph(neighbor)); } } // Return the clone return copies[node]; } // Build graph public static Node BuildGraph() { Node node1 = new Node(0); Node node2 = new Node(1); Node node3 = new Node(2); Node node4 = new Node(3); node1.neighbors.Add(node2); node1.neighbors.Add(node3); node2.neighbors.Add(node1); node2.neighbors.Add(node3); node3.neighbors.Add(node1); node3.neighbors.Add(node2); node3.neighbors.Add(node4); node4.neighbors.Add(node3); return node1; } // Compare two graphs for structural and value equality public static bool CompareGraphs(Node node1 Node node2 Dictionary<Node Node> visited) { if (node1 == null || node2 == null) return node1 == node2; if (node1.val != node2.val || node1 == node2) return false; visited[node1] = node2; if (node1.neighbors.Count != node2.neighbors.Count) return false; for (int i = 0; i < node1.neighbors.Count; i++) { Node n1 = node1.neighbors[i]; Node n2 = node2.neighbors[i]; if (visited.ContainsKey(n1)) { if (visited[n1] != n2) return false; } else { if (!CompareGraphs(n1 n2 visited)) return false; } } return true; } // Driver Code public static void Main() { Node original = BuildGraph(); // Clone the graph using DFS Node cloned = CloneGraph(original); // Compare original and cloned graph bool isEqual = CompareGraphs(original cloned new Dictionary<Node Node>()); Console.WriteLine(isEqual ? 'true' : 'false'); } }
// Definition for a Node class Node { constructor(val = 0) { this.val = val; this.neighbors = []; } } // Map to hold original node to its copy const copies = new Map(); // Function to clone the graph using DFS function cloneGraph(node) { // If the node is NULL return NULL if (node === null) return null; // If node is not yet cloned clone it if (!copies.has(node)) { const clone = new Node(node.val); copies.set(node clone); // Recursively clone neighbors for (let neighbor of node.neighbors) { clone.neighbors.push(cloneGraph(neighbor)); } } // Return the clone return copies.get(node); } // Build graph function buildGraph() { const node1 = new Node(0); const node2 = new Node(1); const node3 = new Node(2); const node4 = new Node(3); node1.neighbors.push(node2 node3); node2.neighbors.push(node1 node3); node3.neighbors.push(node1 node2 node4); node4.neighbors.push(node3); return node1; } // Compare two graphs for structural and value equality function compareGraphs(node1 node2 visited = new Map()) { if (!node1 || !node2) return node1 === node2; if (node1.val !== node2.val || node1 === node2) return false; visited.set(node1 node2); if (node1.neighbors.length !== node2.neighbors.length) return false; for (let i = 0; i < node1.neighbors.length; i++) { const n1 = node1.neighbors[i]; const n2 = node2.neighbors[i]; if (visited.has(n1)) { if (visited.get(n1) !== n2) return false; } else { if (!compareGraphs(n1 n2 visited)) return false; } } return true; } // Driver Code const original = buildGraph(); // Clone the graph using DFS const cloned = cloneGraph(original); // Compare original and cloned graph console.log(compareGraphs(original cloned) ? 'true' : 'false');
Sortir
true


