La probabilité des cartes est la probabilité des événements impliquant un jeu de cartes à jouer. Comme nous le savons, les probabilités sont l’un des sujets importants des mathématiques qui traitent du calcul de la possibilité de tout événement. En termes simples, la probabilité d’une carte est une partie de la probabilité dans laquelle on trouve la probabilité de tirer une carte du jeu de cartes. Dans cet article, nous découvrirons la probabilité de carte avec tous les détails sur le tableau de probabilité de carte, la probabilité de carte à jouer, comment trouver la probabilité de carte et des exemples résolus de probabilité de carte. Commençons notre apprentissage sur le thème de la probabilité des cartes.
Qu’est-ce que la probabilité ?
La probabilité est la branche des mathématiques qui étudie les possibilités qu'un événement se produise ou non. Mathématiquement, ce n'est rien d'autre que le rapport entre le nombre de résultats favorables et le nombre total de résultats (espace échantillon) pour un événement.
Voici quelques exemples concrets de probabilités :
- Jouer à des jeux de cartes, pour trouver la probabilité de gagner ou de perdre la partie.
- Prévisions météo, pour prévoir la pluie.
- Résultats des élections, pour déterminer si le candidat gagnera ou perdra.
- Résultats de l'examen, pour déterminer si le candidat réussira ou échouera.
Formule de probabilité
Si E est un événement avec un espace d'échantillonnage S et que le nombre de résultats favorables est n(E), alors la probabilité de l'événement E, c'est-à-dire P(E), est donnée par :
P(E) = n(E) / n(S)
Qu'est-ce que la probabilité de carte ?
La probabilité de piocher une carte ou une collection de cartes d’un jeu est appelée probabilité de carte. En termes simples, la probabilité liée aux cartes à jouer est appelée probabilité de carte. Comme c'est ce type de probabilité, elle se situe toujours entre 0 et 1. Par exemple, si nous devons trouver la probabilité de tirer un as du jeu de cartes, c'est-à-dire 4/52 = 1/13 [Comme il y a 4 as dans le jeu de 52 cartes].
Jeu de cartes en probabilité
Deck of Cards est une collection de 52 cartes qui semblent exister depuis des milliers d’années. Les jeux de cartes ou les cartes à jouer sont considérés comme originaires d'Inde ou de Chine. La première preuve documentée de ces cartes se trouve en 9èmeChine du XVIIe siècle sous la dynastie Tang. Ces cartes étaient similaires aux cartes modernes et également divisées en quatre couleurs, mais le nom et le symbole de ces couleurs sont différents, c'est-à-dire des pièces de monnaie, des chaînes de pièces, des myriades et des myriades de dizaines.
De nos jours, ces cartes se déclinent en différents modèles et sont divisées en quatre couleurs, à savoir Spade (♠), Club (♣), Heart (❤) et Diamond (◆). Pour une seule carte choisie, l'espace échantillon est de 52, c'est-à-dire que le nombre total de résultats pour une seule carte choisie dans un jeu est de 52.
n(S) pour le jeu de cartes = 52
Types de cartes dans un deck
Tout jeu de cartes peut être classé de plusieurs manières, certains des paramètres selon lesquels les cartes peuvent être classées sont :
- Basé sur les couleurs
- Basé sur les costumes
Comprenons cette classification en détail comme suit :
Basé sur les couleurs
En fonction des couleurs, un jeu de cartes peut être classé en deux catégories :
- Cartons rouges
- Cartes noires
Un total de 52 cartes sont divisées à parts égales en cartes rouges et noires, ce qui signifie qu'il y a 26 cartes rouges et 26 cartes noires dans le jeu.
Basé sur les costumes
Il y a quatre couleurs dans le jeu de cartes :
- Coeurs (❤)
- Diamants (◆)
- Clubs (♣)
- Pique (♠)
En dehors de celles-ci, il existe une autre classification des cartes, basée sur le rang des cartes :
- As
- Cartes numérotées
- Cartes faciales
As
L'As est l'une de ces cartes qui est soit la plus importante, soit la moins importante en fonction du jeu. Cette carte A est écrite dessus et chaque couleur a une de ces cartes, c'est-à-dire quatre cartes as.
Cartes numérotées
De 2 à 10, il y a 9 cartes par couleur, soit un total de 36 cartes de ce type.
Cartes faciales
Les cartes à visage, comme leur nom l'indique, contiennent une figure ou le visage de la figure sur la carte. Il y a trois cartes de chaque couleur, à savoir Jack, Queen, King. Il y a donc un total de 12 figures.
Toutes ces classifications sont visibles dans le tableau suivant.
| Jeu de cartes (52 cartes) | ||||
|---|---|---|---|---|
| Cartes colorées | Cartes noires (26 cartes) | Cartons rouges (26 cartes) | ||
| Costumes | Pique (13 cartes) | Club (13 cartes) | Coeur (13 cartes) | Diamant (13 cartes) |
| Cartes faciales (12 cartes dans un jeu et 3 cartes dans chaque couleur) | K (Roi) | K (Roi) | K (Roi) | K (Roi) |
| Q (Reine) | Q (Reine) | Q (Reine) | Q (Reine) | |
| J (Jack) | J (Jack) | J (Jack) | J (Jack) | |
| Cartes numérotées (36 cartes dans un jeu et 9 cartes dans une couleur) | dix | dix | dix | dix |
| 9 | 9 | 9 | 9 | |
| 8 | 8 | 8 | 8 | |
| 7 | 7 | 7 | 7 | |
| 6 | 6 | 6 | 6 | |
| 5 | 5 | 5 | 5 | |
| 4 | 4 | 4 | 4 | |
| 3 | 3 | 3 | 3 | |
| 2 | 2 | 2 | 2 | |
| Cartes As (4 cartes dans le jeu et 1 carte dans une couleur) | A (As) | A (As) | A (As) | A (As) |
Tableau du jeu de cartes
Le tableau suivant représente la classification du jeu de cartes à jouer :
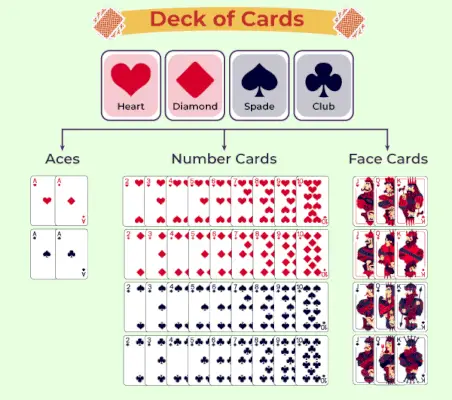
Probabilité des cartes à jouer
Certains des événements courants dans les probabilités de cartes sont présentés dans le tableau suivant :
| Événement E pour la carte à piocher | Probabilité P(E) |
|---|---|
| Un as | P(E) = 4/52 = 1/13 |
| Un roi différenciation partielle dans le latex | P(E) = 4/52 = 1/13 |
| Une carte numérique | P(E) = 36/52 = 9/13 |
| Une carte faciale | P(E) = 12/52 = 3/13 |
| Une carte pique | P(E) = 13/52 = 1/4 |
| Un carton rouge | P(E) = 26/52 = 1/2 |
Comment trouver la probabilité des cartes ?
Les étapes pour trouver la probabilité d'événements impliquant des cartes sont les mêmes que toutes les autres probabilités, qui sont données comme suit :
Étape 1: Tout d’abord, trouvez le nombre de résultats favorables pour la question donnée.
Étape 2: Ensuite, trouvez le nombre total de résultats.
Étape 3: Appliquez la formule de probabilité pour trouver la probabilité de la carte.
Exemple : Quelle est la probabilité de tirer un as d’un jeu de cartes ?
Répondre:
Ici, E est l'événement de tirage d'une carte as
Nombre total de résultats dans un deck n(S) = 52
Nombre de résultats favorables = n(E) = tirer une carte as du jeu = 4 (il y a 4 cartes as dans 1 jeu)
P(E) = n(E) / n(S) = 4/52
P(E) = 1/13
Probabilité de tirer une carte as = 1 / 13
Exemples de questions sur la probabilité des cartes
Problème 1 : Quelle est la probabilité de tirer les cartes suivantes d’un jeu de cartes ?
(i) un chat
(ii) un carton noir
(iii) une carte numérique
Solution:
(i) Ici, E est l'événement de tirage d'une carte à pique
Nombre total de résultats dans un deck n(S) = 52
Nombre de résultats favorables = n(E) = tirer une carte à pique du jeu = 13 (il y a 13 cartes de chaque couleur dans 1 jeu)
P(E) = n(E) / n(S) = 13/52
P(E) = 1 / 4
Probabilité de tirer un pique = 1/4
(ii) Ici, E est l'événement de tirage d'une carte noire
Nombre total de résultats dans un deck n(S) = 52
Nombre de résultats favorables = n(E) = piocher une carte noire du jeu = 26 (il y a 26 cartes noires dans 1 jeu)
P(E) = n(E) / n(S) = 26/52
P(E) = 1 / 2
Probabilité de tirer une carte noire = 1/2
(iii) Ici, E est l'événement de tirage d'une carte numérique
Nombre total de résultats dans un deck n(S) = 52
Nombre de résultats favorables = n(E) = tirer une carte numérique du jeu = 36 (il y a 36 cartes numériques dans 1 jeu)
P(E) = n(E) / n(S) = 36/52
P(E) = 9/13
Probabilité de tirer une carte numérotée = 9 / 13
Problème 2 : Quelle est la probabilité de tirer les cartes suivantes d’un jeu de cartes ?
(i) Un roi ou une carte noire
(ii) Un carton rouge et un as
Solution:
(i) Ici, E est l'événement de tirage d'un roi ou d'une carte noire
Nombre total de résultats dans un deck n(S) = 52
Nombre de résultats favorables = n(E) = tirer un roi ou une carte noire du jeu = 26 + 2 = 28 (Il y a 26 cartes noires dont 2 sont rois et 2 rois noirs restants dans 1 jeu)
P(E) = n(E) / n(S) = 28/52
P(E) = 7/13
Probabilité de tirer un roi ou une carte noire = 7/13
(ii) Ici, E est l'événement de tirage d'une carte rouge et as
Nombre total de résultats dans un deck n(S) = 52
Nombre de résultats favorables = n(E) = tirer une carte rouge et un as du jeu = 2 (il y a 26 cartes rouges dont 2 sont des cartes as)
Selon la question, la carte tirée doit être rouge et as les deux. Donc n(E) = 2
P(E) = n(E) / n(S) = 2 / 52
P(E) = 1/26
Probabilité de tirer une carte rouge et un as = 1 / 26
Problème 3 : Quelle est la probabilité de tirer les cartes suivantes d’un jeu de cartes ?
(i) Une carte hors club
(ii) Une carte sans visage
Solution:
(i) Ici, E est l'événement de tirage d'une carte non-club
Nombre total de résultats dans un deck n(S) = 52
Nombre de résultats favorables = n(E) = piocher une carte sans trèfle du jeu = 39 (il y a 13 trèfles dans 1 jeu, sans jeu = 52 – 13 = 39)
P(E) = n(E) / n(S) = 39/52
P(E) = 3/4
Probabilité de tirer une carte non-club = 3/4
(ii) Ici, E est l'événement de tirage d'une carte sans visage
Nombre total de résultats dans un deck n(S) = 52
Nombre de résultats favorables = n(E) = piocher une carte sans visage du jeu = 40 (il y a 12 cartes avec visage dans 1 jeu, sans jeu = 52 – 12 = 40)
P(E) = n(E) / n(S) = 40/52
P(E) = 10/13
Probabilité de tirer une carte non-club = 10/13
Problème 4 : Quelle est la probabilité de piocher une carte qui n’est ni rouge ni une figure ?
Solution:
Ici, E est l'événement de tirage d'une carte ni rouge ni visage
Nombre total de résultats dans un deck n(S) = 52
jeux d'images sur AndroidNombre de résultats favorables = n(E) = ne tirer ni rouge ni figure du jeu.
Total des cartons rouges = 26
Il y a au total 12 cartes à figures dans un jeu, mais 6 cartes à figures rouges sont déjà retirées. Donc les figures restantes = 12 – 6 = 6
n(E) = 26 + 6 = 32
P(E) = n(E) / n(S) = 32/ 52
P(E) = 8/13
Probabilité de tirer une carte ni rouge ni figure = 8 / 13
Problème 5 : Quelle est la probabilité de tirer deux cartes d'un jeu de cartes avec remplacement lorsque la première carte est un cœur et la deuxième une carte un diamant ?
Solution:
Probabilité de tirer la première carte sous forme de cœur = 13 / 52
Après avoir tiré la première carte, la carte est retirée.
Probabilité de tirer la deuxième carte sous forme de diamant = 13 / 51
Probabilité de tirer la première carte sous forme de cœur et la deuxième sous forme de diamant = (13/52) × (13/51)
Probabilité de tirer la première carte sous forme de cœur et la deuxième sous forme de diamant = 13 / 204
FAQ sur la probabilité des cartes
1. Qu'est-ce que la probabilité de carte ?
La probabilité de tirer une carte du jeu de cartes est appelée probabilité de carte.
2. Répertoriez les types de combinaisons dans un jeu de cartes.
Il existe quatre types de couleurs dans un jeu de cartes. Ils sont:
- Cœurs
- Diamants
- Piques
- Clubs
3. Quel est l'espace d'échantillonnage pour le jeu de cartes lorsqu'une carte est tirée du jeu ?
L'espace échantillon pour le jeu de cartes lorsqu'une carte est tirée contient 52 résultats.
4. Écrivez la formule pour trouver la probabilité.
La formule pour trouver la probabilité est donnée par :
Probabilité d'événement = Nombre d'événements favorables / Nombre total de résultats
OU
P(E) = n(E) / n(S)
5. Combien de cartes faciales y a-t-il dans un jeu de cartes ?
Il y a 12 figures présentes dans un jeu de cartes.
