L'accélération est le changement de vitesse avec le temps. Dans un scénario réel, l’accélération change également avec le temps. Par exemple, vous voyagez d’une ville à une autre par la route. Dans ce cas, vous accélérerez davantage en cas de route vide et ralentirez en cas de circulation. Ce changement d'accélération peut être observé en traçant l'accélération en fonction du temps dans un graphique. C'est ce qu'on appelle le graphique du temps d'accélération. Dans cet article, nous apprendrons en détail le graphique du temps d'accélération et résoudrons les problèmes qui en découlent.
tutoriel hadoop
Qu'est-ce que le graphique du temps d'accélération ?
Un graphique accélération-temps est utilisé pour décrire la relation entre accélération et le temps, où l'accélération est une variable indépendante tracée sur l'axe Y, et le temps est une variable dépendante tracée sur l'axe X. Il est obtenu lorsque les données d'accélération et de temps obtenues sont tracées sur un graphique rectangulaire lors de l'étude du mouvement d'un corps. Nous pouvons déterminer le changement de vitesse dans un intervalle de temps donné à l’aide d’un graphique accélération-temps. En déterminant l'aire sous la courbe du graphique accélération-temps, nous pouvons trouver le changement de vitesse d'un objet en mouvement sur une certaine période.
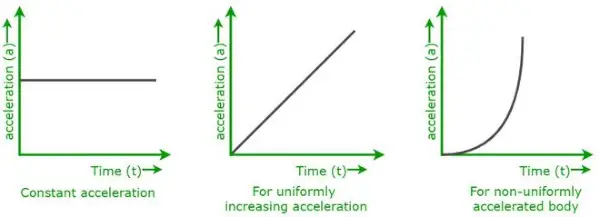
Les graphiques présentés ci-dessus sont des graphiques accélération-temps pour différents types de mouvements corporels.
- Lorsqu'un corps se déplace avec une accélération constante,
- Lorsqu'un corps se déplace uniformément avec une accélération croissante.
- Lorsqu'un corps se déplace de manière non uniforme avec une accélération variable.
Conclusions
Voici les points conclus à partir des graphiques temps d’accélération.
- La pente du graphique accélération-temps est △a/△t.
- La zone sous le graphique accélération-temps représente le changement de vitesse.
Laisser,
△v soit le changement de vitesse,
△a être le changement d'accélération,
△t être le changement dans le temps.
Maintenant, l'aire sous la courbe = △v
Nous savons que l’accélération d’un corps est appelée le taux de changement de vitesse sur une période de temps donnée.
Donc,
△a = △v/△t
Maintenant, en multipliant par △t des deux côtés, nous obtenons :
△v = △a × △t (v qui est l'aire sous la courbe en temps d'accélération graphique )
- Pour un objet se déplaçant avec une accélération constante, c’est-à-dire que l’accélération est la même à tous les intervalles de temps. Par conséquent, la pente du graphique accélération-temps est nulle et le graphique sera parallèle à l’axe du temps.
Accélération vs retard

Accélération: L’accélération d’un corps est appelée le taux de changement de vitesse au cours d’une période de temps donnée. C'est une quantité vectorielle et elle est mesurée en termes de m/s2.
Accélération = Changement de vitesse/temps
ici, le changement de vitesse est positif.
Supposons qu'un corps qui se déplace à une vitesse uniforme augmente sa vitesse. Le taux d’augmentation de la vitesse est appelé accélération d’un corps. Soit u la vitesse initiale, v la vitesse finale et t l'intervalle de temps, alors l'accélération du corps est donnée par :
Accélération (a) = (v – u)/t
Exemple: Un exemple d’accélération dans la vie quotidienne est de tourner une voiture dans un virage. La vitesse de la voiture augmente à mesure que la direction change, ce qui entraîne une accélération. L'accélération augmente avec l'augmentation de la vitesse de virage.
Retardement: Le retard d’un corps est appelé le taux de changement de vitesse au cours d’une période de temps donnée. Un retard signifie une accélération négative.
Retardement = Changement de vitesse/temps
ici, le changement de vitesse est négatif.
Supposons qu'un corps qui se déplace à une vitesse uniforme diminue sa vitesse. Le taux de diminution de la vitesse est appelé retard d’un corps. Soit u la vitesse initiale, v la vitesse finale et t l'intervalle de temps, alors le retard du corps est donné par :
Retard = (v – u)/t
Exemple: Un exemple concret de retard consiste à éteindre un ventilateur. Lorsque l’interrupteur du ventilateur mobile est éteint, la vitesse de rotation des pales du ventilateur ralentit progressivement. Ce taux de réduction de la vitesse du ventilateur est appelé retard.
Vérifiez également ceci :
- Graphiques de temps de distance
- Graphiques de vitesse et de temps
Exemples de problèmes sur les graphiques de temps d'accélération
Problème 1 : À partir du graphique accélération en fonction du temps ci-dessous, déterminez le changement de vitesse.

Solution:
Pour trouver le changement de vitesse du corps, nous devons déterminer l’aire sous la courbe.
Ainsi, pour trouver la variation de la vitesse de l’objet, nous devons calculer l’aire du triangle.
△v = aire du triangle
= ½ × 25 × 6
△v = 75 m/s.
La variation de vitesse est donc de 75 m/s.
Problème 2 : À partir du graphique accélération en fonction du temps ci-dessous, trouvez la vitesse initiale d'un corps si sa vitesse finale est de 55 m/sec.

Solution:
Pour trouver le changement de vitesse du corps, nous devons déterminer l’aire sous la courbe. Sur le graphique, nous pouvons observer qu’il comporte un rectangle et un triangle. Ainsi, pour trouver la variation de la vitesse de l’objet, nous devons calculer l’aire de ces figures.
△v = aire du triangle + aire du rectangle
= ½ × 8 × 6 + 2 × 8
△v = 24 + 16 = 42 m/s
Nous savons que,
△v = vitesse finale – vitesse initiale
42 = 55 – poje
dansje= 55 – 42 = 13 m/s
La vitesse initiale est donc de 13 m/s.
Problème 3 : À partir du graphique accélération en fonction du temps ci-dessous, déterminez la vitesse à t = 6 secondes, si v(0) = 0.

Solution:
L'accélération est donnée par :
a = dv/dt
⇒ dv = (a)dt
En intégrant des deux côtés, on obtient
∫dv = ∫(a)dt
⇒v = ∫(1,5)dt
⇒ v(t) = 1,5t + c, où c est une constante
⇒v(0) = 0
⇒ c = 0
Maintenant, v(t) = 1,5t
v(6) = 1,5 × 6 = 9 m/s
Par conséquent, la vitesse à t = 6 secondes est de 9 m/s.
Problème 4 : Qu'indique l'aire sous le graphique du temps d'accélération ?
Solution:
La zone sous le graphique accélération-temps représente le changement de vitesse.
Soit △v le changement de vitesse, △a le changement d'accélération et △t le changement de temps.
Maintenant, l'aire sous la courbe = △v
Nous savons que l’accélération d’un corps est appelée le rapport de la variation de vitesse sur une période de temps donnée.
Donc,
△a = △v/△t
Maintenant, en multipliant par △t des deux côtés, nous obtenons :
△v = △a × △t
Ainsi, l’aire sous la courbe est obtenue en multipliant le changement d’accélération et le changement de temps.
Problème 5 : Que signifie une secousse dans le graphique du temps d'accélération ?
Solution:
Une secousse est le changement soudain de l'accélération du corps en mouvement, et la pente du graphique a-t représente la secousse.
La pente du graphique accélération-temps = jerk = △a/△t
Graphique du temps d'accélération – FAQ
Qu'est-ce qu'un graphique temps d'accélération ?
Un graphique accélération-temps affiche la façon dont l’accélération varie dans le temps pour un objet se déplaçant en ligne droite. Il trace l'accélération sur l'axe des y en fonction du temps sur l'axe des x.
Comment calculer l’aire sous un graphique temps d’accélération et que représente-t-elle ?
La zone sous un graphique accélération-temps représente le changement de vitesse sur la période couverte par le graphique. Pour calculer cette aire, vous additionnerez généralement les aires des rectangles ou des trapèzes qui s'inscrivent sous la courbe, qui correspondent à des intervalles de temps distincts pendant lesquels l'accélération est constante.
Pouvez-vous déterminer la vitesse d’un objet à un moment précis à partir d’un graphique accélération-temps ?
Il n'est pas possible de déterminer directement la vitesse instantanée à un instant précis à partir d'un graphique accélération-temps. Cependant, vous pouvez calculer le changement de vitesse sur une période de temps en recherchant la zone sous le graphique au cours de cette période. Connaître la vitesse initiale permet de déterminer la vitesse finale.
Qu’indique une accélération négative sur ce type de graphique ?
Une accélération négative sur un graphique accélération-temps indique une décélération, où la vitesse de l'objet diminue si l'objet se déplace dans la direction positive. Si l’objet se déplace dans une direction considérée comme négative, alors une accélération négative implique une augmentation de la vitesse.
Comment pouvez-vous trouver l’accélération moyenne à partir d’un graphique temps d’accélération ?
L'accélération moyenne peut être déterminée en trouvant le changement total de vitesse (en additionnant les zones sous la courbe, en tenant compte de la direction) et en le divisant par l'intervalle de temps total. Visuellement, cela peut être représenté comme un rectangle dont l'aire est équivalente à l'aire totale sous le graphique accélération-temps.
Que représente la pente d’un graphique accélération-temps ?
La pente d'un graphique accélération-temps indique le taux de variation de l'accélération dans le temps, appelé secousse. Une pente raide implique un changement rapide d’accélération.
Comment représenter un corps au repos sur un graphique accélération-temps ?
Un corps au repos ou en mouvement à vitesse constante est représenté sur un graphique accélération-temps par une ligne le long de l'axe du temps à une accélération nulle.
Comment interpréter un graphique accélération-temps ?
La pente d'un graphique accélération-temps représente le taux de changement de l'accélération, une pente plus raide indiquant un taux de changement plus élevé.
Que représente l’aire sous un graphique temps d’accélération ?
L'aire sous la courbe sur un graphique accélération-temps représente le changement de vitesse de l'objet. Plus précisément, cela représente la vitesse finale moins la vitesse initiale.
