Score Z dans les statistiques est une mesure du nombre d'écarts types entre un point de données et la moyenne d'une distribution. Trouvons le score z dans les statistiques. Un score z de 0 indique que le score du point de données est le même que le score moyen. Un score z positif indique que le point de données est supérieur à la moyenne, tandis qu'un score z négatif indique que le point de données est inférieur à la moyenne.

La formule pour calculer un z-score est la suivante : z = (x – µ)/ p

Où:

• X: est la valeur de test
• m: est la moyenne
• à: est la valeur standard

Dans cet article, nous allons aborder les concepts suivants :

Table des matières

• Qu’est-ce que le Z-Score ?
• Comment calculer le score Z ?
• Caractéristiques du Z-Score
• Calculer les valeurs aberrantes à l'aide de la valeur du score Z
• Implémentation de Z-Score en Python
• Application du score Z
• Scores Z par rapport à l'écart type
• Pourquoi les scores Z sont-ils appelés scores standards ?

Qu’est-ce que le Z-Score ?

Le score Z, également connu sous le nom de score standard, nous indique l'écart d'un point de données par rapport à la moyenne en l'exprimant en termes d'écarts types au-dessus ou en dessous de la moyenne. Cela nous donne une idée de la distance entre un point de données et la moyenne. Par conséquent, le Z-Score est mesuré en termes d’écart type par rapport à la moyenne. Par exemple, un score Z de 2 indique que la valeur est à 2 écarts types de la moyenne. Pour utiliser un score z, nous devons connaître la moyenne de la population (μ) ainsi que l'écart type de la population (σ).

La formule du Z-Score

Un score z peut être calculé à l’aide de la formule suivante.

z = (X – µ) / p

où,

• z = score Z
• X = Valeur de l'élément
• μ = moyenne de la population
• σ = écart type de la population

Comment calculer le score Z ?

On nous donne la moyenne de la population (μ), l'écart type de la population (σ) et la valeur observée (x) dans l'énoncé du problème en la remplaçant dans l'équation du score Z nous donne la valeur du score Z. Selon que le Z-Score donné est positif ou négatif, nous pouvons utiliser Tableau Z positif ou Tableau Z négatif disponible en ligne ou au dos de votre manuel de statistiques en annexe.

Exemple 1:

Vous passez l'examen GATE et obtenez un score de 500. Le score moyen pour le GATE est de 390 et l'écart type est de 45. Quel a été votre score au test par rapport au candidat moyen ?

tri à bulles java

Solution:

Les données suivantes sont facilement disponibles dans l'énoncé de la question ci-dessus

Score brut/valeur observée = X = 500

Score moyen = μ = 390

Écart type = σ = 45

En appliquant la formule du z-score,

z = (X – µ) / p

z = (500 – 390) / 45

z = 110/45 = 2,44

paramètres Java par défaut

Cela signifie que votre z-score est 2.44 .

Puisque le Z-Score est positif à 2,44, nous utiliserons le Z-Table positif.

Jetons maintenant un coup d'œil à Tableau Z (CC-BY) pour connaître vos résultats par rapport aux autres candidats.

Suivez les instructions ci-dessous pour trouver la probabilité dans le tableau.

Ici, score z = 2,44, lequel je indique que le point de données est de 2,44 écarts types au-dessus de la moyenne.

1. Tout d’abord, mappez les deux premiers chiffres 2,4 sur l’axe Y.
2. Puis le long de l'axe X, carte 0,04
3. Joignez les deux axes. L’intersection des deux vous fournira la probabilité cumulée associée à la valeur du score Z que vous recherchez

[Cette probabilité représente l'aire sous la courbe normale standard à gauche du score Z]

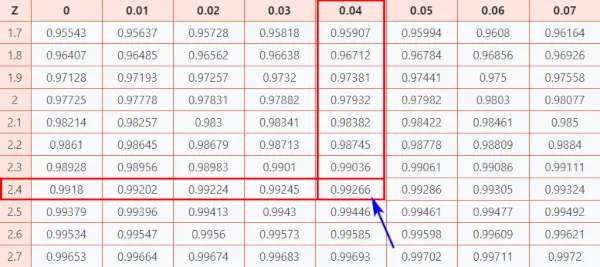
Tableau de distribution normale

En conséquence, vous obtiendrez la valeur finale qui est 0,99266 .

Nous devons maintenant comparer notre score initial de 500 à l’examen GATE par rapport au score moyen du lot. Pour ce faire, nous devons convertir la probabilité cumulée associée au score Z en une valeur en pourcentage.

0,99266 × 100 = 99,266 %

Enfin, vous pouvez dire que vous avez bien performé que presque 99% des autres candidats.

Exemple 2 : Quelle est la probabilité qu'un élève obtienne entre 350 et 400 (avec un score moyen μ de 390 et un écart type σ de 45) ?

Solution:

Note minimale = X₁= 350

Note maximale = X₂= 400

En appliquant la formule du z-score,

Avec₁= (X1 – m) /p

Avec₁= (350 – 390) / 45

Avec₁= -40 / 45 = -0,88

Avec₂= (X₂– m)/p

z2 = (400 – 390) / 45

Avec₂= 10 / 45 = 0,22

interface comparable en java

Puisque z1 est négatif, nous devrons regarder un négatif Table Z et trouvons que la probabilité cumulée p1, la première probabilité, est 0,18943 .

Avec₂est positif, nous utilisons donc une table Z positive qui donne une probabilité cumulée p₂de 0,58706 .

La probabilité finale est calculée en soustrayant p1 de p₂:

p = p₂–p₁

p = 0,58706 – 0,18943 = 0,39763

La probabilité qu'un élève obtienne entre 350 et 400 est 39,763% (0,39763 * 100).

Caractéristiques du Z-Score

• L'ampleur du score Z reflète la distance entre un point de données et la moyenne en termes d'écarts types.
• Un élément ayant un score z inférieur à 0 signifie que l'élément est inférieur à la moyenne.
• Les scores Z permettent de comparer des points de données provenant de différentes distributions.
• Un élément ayant un score z supérieur à 0 signifie que l'élément est supérieur à la moyenne.
• Un élément ayant un score z égal à 0 représente que l'élément est égal à la moyenne.
• Un élément ayant un score z égal à 1 représente que l'élément est supérieur de 1 écart type à la moyenne ; un z-score égal à 2, 2 écarts types supérieurs à la moyenne, et ainsi de suite.
• Un élément ayant un score z égal à -1 représente que l'élément est inférieur de 1 écart type à la moyenne ; un z-score égal à -2, 2 écarts types inférieurs à la moyenne, et ainsi de suite.
• Si le nombre d’éléments dans un ensemble donné est grand, alors environ 68 % des éléments ont un score z compris entre -1 et 1 ; environ 95 % ont un z-score compris entre -2 et 2 ; environ 99 % ont un score z compris entre -3 et 3. Ceci est connu sous le nom de règle empirique et indique le pourcentage de données dans certains écarts types par rapport à la moyenne dans une distribution normale, comme le montre l'image ci-dessous.

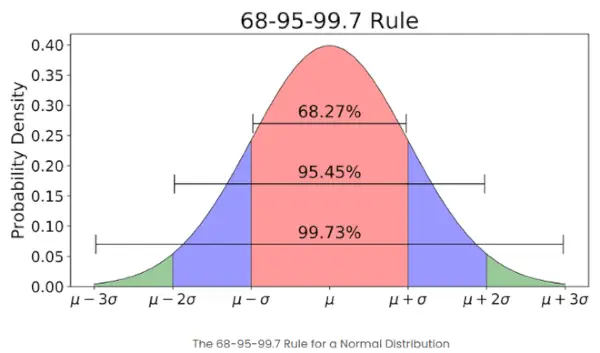
La règle empirique dans la distribution normale

Calculer les valeurs aberrantes à l'aide de la valeur du score Z

Nous pouvons calculer les valeurs aberrantes dans les données en utilisant la valeur du score z des points de données. Les étapes pour considérer un point de données aberrant sont les suivantes :

• Dans un premier temps, nous rassemblons l'ensemble de données dans lequel nous voulons voir les valeurs aberrantes
• Nous calculerons la moyenne et l'écart type de l'ensemble de données. Ces valeurs seront utilisées pour calculer la valeur du score z de chaque point de données.
• Nous calculerons la valeur du score z pour chaque point de données. La formule de calcul de la valeur du score z sera la même que
  Z = frac{{X – mu}}{{sigma}}
  où X sera le point de données, μ est la moyenne des données et σ est l'écart type de l'ensemble de données.
• Nous déterminerons la valeur seuil du score z après laquelle le point de données pourrait être considéré comme une valeur aberrante. Cette valeur seuil est un hyperparamètre que nous décidons en fonction de notre projet.
• Un point de données dont la valeur du score z est supérieure à 3 signifie que le point de données n'appartient pas au point 99,73 % de l'ensemble de données.
• Tout point de données dont le score z est supérieur à notre valeur seuil décidée sera considéré comme une valeur aberrante.

Vérifier: Score Z pour la détection des valeurs aberrantes

Implémentation de Z-Score en Python

Nous pouvons utiliser Python pour calculer la valeur du score z des points de données dans l'ensemble de données. Nous utiliserons également la bibliothèque numpy pour calculer la moyenne et l'écart type de l'ensemble de données.

Sortir:

Score Z : [-0,7574907 -0,59097335 -0,20243286 0,35262498 0,6301539 -0,72973781
-0,70198492 -0,00816262 0,13060185 0,54689523 1,10195307 3,32218443
-0,67423202 -0,64647913 -0,61872624 -0,59097335 -0,56322046]
Les valeurs aberrantes dans l'ensemble de données sont [150]

Application du score Z

• Les scores Z sont souvent utilisés pour la mise à l'échelle des fonctionnalités afin de regrouper différentes fonctionnalités sur une échelle commune. La normalisation des fonctionnalités garantit qu'elles ont une moyenne et une variance unitaire nulles, ce qui peut être bénéfique pour certains algorithmes d'apprentissage automatique, en particulier ceux qui reposent sur des mesures de distance.
• Les scores Z peuvent être utilisés pour identifier les valeurs aberrantes dans un ensemble de données. Les points de données dont les scores Z dépassent un certain seuil (généralement 3 écarts types par rapport à la moyenne) peuvent être considérés comme des valeurs aberrantes.
• Les scores Z peuvent être utilisés dans les algorithmes de détection d'anomalies pour identifier les instances qui s'écartent considérablement du comportement attendu.
• Les scores Z peuvent être appliqués pour transformer des distributions asymétriques en distributions plus normales.
• Lorsque vous travaillez avec des modèles de régression, les scores Z des résidus peuvent être analysés pour vérifier l'homoscédasticité (variance constante des résidus).
• Les scores Z peuvent être utilisés dans la mise à l'échelle des caractéristiques en examinant leurs écarts types par rapport à la moyenne.

Scores Z par rapport à l'écart type

Vérifier: Tableau des scores Z

Pourquoi les scores Z sont-ils appelés scores standards ?

Les scores Z sont également appelés scores standard car ils standardisent la valeur d'une variable aléatoire. Cela signifie que la liste des scores standardisés a une moyenne de 0 et un écart type de 1,0. Les scores Z permettent également de comparer les scores sur différents types de variables. En effet, ils utilisent la position relative pour égaliser les scores de différentes variables ou distributions.

Les scores Z sont fréquemment utilisés pour comparer une variable à une distribution normale standard (avec μ = 0 et σ = 1).

Z-Score dans les statistiques – FAQ

Quelle est la signification des Z-Scores positifs et négatifs ?

Les scores Z positifs indiquent des valeurs supérieures à la moyenne, tandis que les scores Z négatifs indiquent des valeurs inférieures à la moyenne. Le signe reflète la direction de l'écart par rapport à la moyenne.

Que signifie un Z-Score de 0 ?

Un score Z de 0 indique que la valeur du point de données se situe exactement à la moyenne de l'ensemble de données. Cela suggère que le point de données n'est ni au-dessus ni en dessous de la moyenne.

Quelle est la règle 68-95-99.7 par rapport aux Z-Scores ?

La règle 68-95-99.7, également connue sous le nom de règle empirique, stipule que :

types de tests de logiciels

• Environ 68 % des données se situent à moins d’un écart type de la moyenne.
• Environ 95 % se situent dans une fourchette de 2 écarts types.
• Environ 99,7 % se situent dans 3 écarts types.

Les Z-Scores peuvent-ils être utilisés pour des distributions non normales ?

Les scores Z reposent sur l’hypothèse que les données suivent une distribution normale. Cependant, en pratique, les Z-Scores sont bénéfiques pour les données qui suivent une distribution normale. Bien que les scores Z puissent être calculés pour n'importe quelle distribution, leur interprétation devient moins fiable et moins simple lorsqu'il s'agit de données non distribuées normalement.

Comment les Z-Scores peuvent-ils être appliqués dans des situations réelles ?

Les Z-Scores ont diverses applications, telles que la finance pour l'analyse de portefeuille, l'éducation pour les tests standardisés, la santé pour les évaluations cliniques, etc. Ils fournissent une mesure standardisée pour comparer et interpréter les données.