Surface d'un prisme : En mathématiques, un prisme est un membre essentiel de la famille des polyèdres et est défini comme une forme tridimensionnelle comportant deux polygones identiques se faisant face et reliés latéralement par des faces rectangulaires ou parallélogrammes. Les polygones identiques peuvent être des triangles, des carrés, des rectangles, des pentagones ou tout autre polygone à n côtés et sont appelés bases du prisme. Les autres faces d'un prisme sont des parallélogrammes ou des rectangles.
Dans cet article, nous discuterons différents types de prismes et la surface de la formule du prisme, avec des exemples et des problèmes pratiques.
Table des matières
- Quelle est la surface du prisme ?
- Différents types de prisme
- Surface de la formule du prisme
- Surface d'un prisme Exemples résolus
- Problèmes de pratique sur la surface d'un prisme
Quelle est la surface du prisme ?
La surface d’un prisme est appelée la surface totale délimitée par toutes ses faces. Pour déterminer la surface d’un prisme, nous devons calculer les aires de chacune de ses faces, puis additionner les aires résultantes. Un prisme a deux types de surfaces, à savoir la surface latérale et la surface totale. La surface occupée par les faces d’un prisme, à l’exclusion des deux faces parallèles (bases d’un prisme), est appelée surface latérale.
La surface latérale d'un prisme = [Périmètre de base × hauteur] unités carrées
Or, la surface totale d’un prisme est la somme des aires de ses deux bases et de sa surface latérale.
La formule générale pour calculer la surface totale de tout type de prisme droit est la suivante :
La surface totale d'un prisme = [2 (surface de base) + (périmètre de base × hauteur)] unités carrées
Différents types de prisme
Il existe différents types de prismes en fonction de la forme de la base d'un prisme, comme
- Prismes triangulaires,
- Prismes carrés,
- Prismes rectangulaires,
- Prismes pentagonaux,
- Prismes hexagonaux,
- Prismes octogonaux.
Prisme triangulaire
Un prisme à base triangulaire est appelé prisme triangulaire. Un prisme triangulaire se compose de trois surfaces rectangulaires inclinées et de deux bases triangulaires parallèles. Soit H la hauteur du prisme triangulaire ; a, b et c sont les longueurs des côtés et h est la hauteur des bases triangulaires.
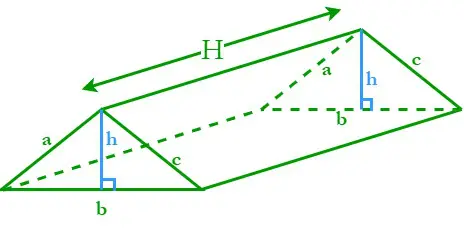
Le périmètre d'une base triangulaire (P) = Somme de ses trois côtés = a + b + c
L'aire d'une base triangulaire (A) = ½ × base × hauteur = ½ bh
Nous savons que la formule générale du La surface latérale d'un prisme droit est L. S. A. = PH, où P est le périmètre de base et A est la surface de base.
En substituant toutes les valeurs de la formule générale, nous obtenons ,
La surface latérale d'un prisme triangulaire = (a + b + c)H unités carrées
où,
a, b, c sont les côtés d'une base triangulaire
H est la hauteur du prisme triangulaire
Nous savons que la formule générale de la surface totale d’un prisme droit est T. S. A. = PH+2A, où P est le périmètre de base, A est la surface de base et H est la hauteur du prisme.
En substituant toutes les valeurs de la formule générale, nous obtenons
La surface totale du prisme triangulaire = (a + b + c)H + 2 × (½ bh)
La surface totale du prisme triangulaire = (a + b + c)H + bh unités carrées
où,
a, b, c sont les côtés d'une base triangulaire
H est la hauteur du prisme triangulaire
h est la hauteur du triangle
Prisme rectangulaire
Un prisme à base rectangulaire est appelé prisme rectangulaire. Un prisme rectangulaire se compose de quatre surfaces rectangulaires et de deux bases rectangulaires parallèles. Soit la hauteur du prisme h et la longueur et la largeur de ses bases rectangulaires respectivement l et w. .

Le périmètre d'une base rectangulaire (P) = Somme de ses quatre côtés = 2 (l + w)
L'aire d'une base rectangulaire (A) = longueur × largeur = l × w
Nous savons que la formule générale pour la surface latérale d’un prisme droit est L. S. A. = PH, où P est le périmètre de base et A est la surface de base.
En substituant toutes les valeurs de la formule générale, nous obtenons ,
La surface latérale d'un prisme rectangulaire = 2h(l + w) unités carrées
où,
l est la longueur
w est la largeur
sa taille
Nous savons que la formule générale pour la surface totale d'un prisme droit est T.S.A. = PH+2A, où P est le périmètre de base, A est la surface de base et H est la hauteur du prisme.
En substituant toutes les valeurs de la formule générale, nous obtenons
La surface totale du prisme rectangulaire = 2h(l + w) + 2(l × w)
= 2 gauche + 2 blancs + 2 blancs
La surface totale du prisme rectangulaire = 2 (lh + wh + lw) unités carrées
où,
l est la longueur
w est la largeur
sa taille
Prisme carré
Un prisme à base carrée est appelé prisme carré. Un prisme carré se compose de quatre surfaces rectangulaires et de deux bases carrées parallèles. Soit la hauteur du prisme h et la longueur de ses bases carrées s.

Le périmètre d'une base carrée (P) = Somme de ses quatre côtés = s + s + s + s = 4s
L'aire d'une base carrée (A) = (longueur du côté)2= s2
Nous savons que la formule générale pour la surface latérale d’un prisme droit est L. S. A. = PH, où P est le périmètre de base et A est la surface de base.
En substituant toutes les valeurs de la formule générale que nous obtenons,
La surface latérale d'un prisme carré = 4sh unités carrées
où,
s est le côté de la base carrée
h est la hauteur du prisme carré
Nous savons que la formule générale de la surface totale d’un prisme droit est T.S.A. = PH+2A, où P est le périmètre de base, A est la surface de base et H est la hauteur du prisme.
En substituant toutes les valeurs de la formule générale, on obtient
La surface totale du prisme carré = [4sh + 2s 2 ] unités carrées
où,
s est le côté de la base carrée
h est la hauteur du prisme carré
Prisme Pentagonal
Un prisme à base pentagonale est appelé prisme pentagonal. Un prisme pentagonal se compose de cinq surfaces rectangulaires inclinées et de deux bases pentagonales parallèles. Soit h la hauteur du prisme pentagonal ; a et b sont la longueur de l'apothème et les longueurs des côtés des bases pentagonales.

Le périmètre d'une base de pentagone (P) = Somme de ses cinq côtés = 5b
L'aire d'une base de pentagone (A) = 5/2 x (longueur de l'apothème) x (longueur du côté) = 5ab
Nous savons que la formule générale pour la surface latérale d’un prisme droit est L. S. A. = PH, où P est le périmètre de base et A est l’aire de base.
En substituant toutes les valeurs de la formule générale que nous obtenons,
La surface latérale d'un prisme pentagonal = 5bh unités carrées
où,
b est le côté de la base pentagonale
h est la hauteur du prisme pentagonal
Nous savons que la formule générale pour la surface totale d'un prisme droit est T. S. A. = PH + 2A, où P est le périmètre de la base, A est la surface de la base et H est la hauteur du prisme.
En substituant toutes les valeurs de la formule générale que nous obtenons,
La surface totale du prisme pentagonal = [5bh + 5ab] unités carrées
où,
b est le côté de la base pentagonale
a est la longueur de l'apothème.
h est la hauteur du prisme pentagonal
Prisme Hexagonal
Un prisme à base hexagonale est appelé prisme hexagonal. Un prisme hexagonal se compose de six surfaces rectangulaires inclinées et de deux bases hexagonales parallèles. Soit h la hauteur du prisme hexagonal ; a soit les longueurs des côtés des bases hexagonales.

Le périmètre d'une base hexagonale (P) = Somme de ses six côtés = 6a
L'aire d'une base hexagonale (A) = 6 x (Aire d'un triangle équilatéral)
A = 6 x (√3a2/4) ⇒ UNE = 3√3a2/2
Nous savons que la formule générale pour la surface latérale d’un prisme droit est L. S. A. = PH, où P est le périmètre de base et A est l’aire de base.
En substituant toutes les valeurs de la formule générale que nous obtenons,
La surface latérale d'un prisme hexagonal = 6ah unités carrées
où,
a est le côté de la base hexagonale
h est la hauteur de la base hexagonale
Nous savons que la formule générale pour la surface totale d'un prisme droit est T.S.A. = PH+2A, où P est le périmètre de base, A est la surface de base et H est la hauteur du prisme.
En substituant toutes les valeurs de la formule générale, nous obtenons
La surface totale du prisme hexagonal = [6ah +3√3a2] unités carrées
où,
a est le côté de la base hexagonale
h est la hauteur de la base hexagonale :
Surface de la formule du prisme
Le tableau ci-dessous fournit la formule pour différents types de prismes :
Forme | Base du prisme | Surface latérale[Périmètre de base × hauteur] | Superficie totale[(2 × Surface de base) + (Périmètre de base × hauteur)] |
|---|---|---|---|
Prisme triangulaire | Triangle statut git | (a + b + c)H unités carrées | (a + b + c)H + bh unités carrées |
Prisme rectangulaire | Rectangle | 2h(l + w) unités carrées | 2 (lh + wh + lw) unités carrées |
Prisme carré | Carré | Unités carrées de 4sh | [4sh + 2s2] unités carrées |
Prisme Pentagonal | Pentagone | Unités carrées de 5 ch | [5ab + 5bh] unités carrées |
Prisme Hexagonal | Hexagone | Unités carrées de 6ah | [3√3a2+ 6ah] unités carrées |
Surface d'un prisme Exemples résolus
Problème 1 : Quelle est la hauteur d'un prisme dont l'aire de base est de 36 unités carrées, son périmètre de base est de 24 unités et sa surface totale est de 320 unités carrées ?
Solution:
Compte tenu des données,
Superficie de base = 36 unités carrées
Périmètre de base = 24 unités
La surface totale du prisme = 320 unités carrées
Nous avons,
La surface totale du prisme = (2 × surface de base) + (périmètre de base × hauteur)
⇒ 320 = (2 × 36)+ (24 × h)
⇒ 24h = 248 ⇒ h = 10,34 unités
La hauteur du prisme donné est donc de 10,34 unités.
Problème 2 : Trouvez la surface totale d'un prisme carré si la hauteur du prisme et la longueur du côté de la base carrée sont respectivement de 13 cm et 4 cm.
Solution:
Compte tenu des données,
La hauteur du prisme carré (h) = 13 cm
La longueur du côté de la base carrée (a) = 4 cm
Nous savons que,
La surface totale d'un prisme carré = 2a2+ 4ah
= 2 × (4)2+ 4 × 4 × 13
= 32 + 208 = 240 cm2
La surface totale du prisme donné est donc de 240 cm².
Problème 3 : Déterminer la longueur de base d'un prisme pentagonal si sa superficie totale est de 100 unités carrées et sa hauteur et sa longueur d'apothème sont respectivement de 8 unités et 5 unités.
Solution:
Compte tenu des données,
La surface totale du prisme pentagonal = 100 unités carrées
La hauteur du prisme (h) = 8 unités
Longueur de l'apothème (a) = 5 unités
Nous savons que,
La surface totale du prisme pentagonal = 5ab + 5bh
⇒ 100 = 5b (a+h)
⇒ 100/5 = b (5 + 8)
⇒ 20 = b × (13) ⇒ b = 25/16 = 1,54 unités
La longueur de base est donc de 1,54 unités.
Problème 4 : Déterminez la hauteur du prisme rectangulaire et la superficie totale d'un prisme rectangulaire si sa surface latérale est de 540 cm2 et que la longueur et la largeur de la base sont respectivement de 13 cm et 7 cm.
Solution:
bonne chance
Compte tenu des données,
La longueur de la base rectangulaire (l) = 13 cm
La largeur de la base rectangulaire (w) = 7 cm
La surface latérale du prisme = 540 cm²
Nous avons,
La surface latérale du prisme = périmètre de base × hauteur
⇒ 540 = 2 (l + w)h
⇒ 2 (13 + 7) h = 540
⇒ 2 (20) h = 540 ⇒ h = 13,5 cm
Nous savons que,
La surface totale du prisme rectangulaire = 2 (lw + wh + lh)
= 2 × (13 × 7 + 7 × (13,5) + 13 × (13,5))
= 2 × (91 + 94,5 + 175,5) = 722 cm²
Par conséquent, la hauteur et la surface totale du prisme rectangulaire donné sont respectivement de 13,5 cm et 722 cm².
Problème 5 : Déterminez la surface du prisme hexagonal régulier si la hauteur du prisme est de 12 pouces et la longueur du côté de la base est de 5 pouces.
Solution:
Compte tenu des données,
La hauteur du prisme (h) = 12 po
La longueur du côté de la base (a) = 6 po
La surface d'un prisme hexagonal régulier = 6ah + 3√3a2
= 6 × 5 × 12 + 3√3(5)2
= 360 + 75√3
= 360 + 75 × (1,732) = 489,9 pouces carrés
Par conséquent, la surface du prisme donné est de 489,9 pouces carrés.
Problème 6 : Calculez les surfaces latérales et totales d'un prisme triangulaire dont le périmètre de base est de 25 pouces, la longueur et la hauteur de la base du triangle sont de 9 pouces et 10 pouces et la hauteur du prisme est de 14 pouces.
Solution:
Compte tenu des données,
La hauteur du prisme (H) = 14 pouces
Le périmètre de base du prisme (P) = 25 pouces
La longueur de base du triangle = 9 pouces
La hauteur du triangle = 10 pouces
Nous savons que,
La surface latérale du prisme = périmètre de base × hauteur
= 25 × 14 = 350 pouces carrés
Aire de la base triangulaire (A) = ½ × base × hauteur = 1/2 × 9 × 10 = 45 po²
La surface totale du prisme triangulaire = 2A + PH
= 2 × 45 + 25 × 14 = 90 + 350 = 440 pouces carrés
Par conséquent, les surfaces latérales et totales du prisme sont respectivement de 350 pouces carrés et 440 pouces carrés.
Problèmes pratiques sur la surface d’un prisme
1. Étant donné un prisme rectangulaire de dimensions :
- Longueur = 6 cm
- Largeur = 4 cm
- Hauteur = 5 cm
Calculez la superficie totale.
2. Considérons un prisme triangulaire de dimensions :
- Base du triangle = 8 cm
- Hauteur du triangle = 6 cm
- Longueur du prisme = 10 cm
Trouvez la superficie totale.
3. Déterminez l’aire d’un prisme pentagonal régulier avec :
- Longueur côté de la base = 7 cm
- Hauteur du prisme = 9 cm.
4. Calculez la surface d’un prisme hexagonal avec :
- Longueur du côté de la base hexagonale régulière = 10 cm
- Hauteur du prisme = 12 cm.
Surface d'un prisme – FAQ
Qu'est-ce qu'un prisme en géométrie ?
Un prisme est une forme tridimensionnelle avec deux bases parallèles congruentes et des faces latérales rectangulaires ou parallélogrammes les reliant. Les prismes se présentent sous diverses formes, telles que les prismes rectangulaires, les prismes triangulaires et les prismes pentagonaux, chacun ayant des caractéristiques uniques.
Comment trouver la surface d’un prisme ?
Pour trouver l’aire d’un prisme, calculez les aires de toutes ses faces, puis additionnez-les. Pour un prisme rectangulaire, la formule de la surface est 2lw + 2lh + 2wh, où l est la longueur, w est la largeur et h est la hauteur. Pour d'autres types de prismes, tels que les prismes triangulaires ou pentagonaux, des formules supplémentaires pour l'aire de base et l'aire latérale peuvent être nécessaires.
Quelles sont les propriétés d'un prisme ?
Les prismes ont plusieurs propriétés clés :
- Ils ont deux bases parallèles congruentes.
- Les faces latérales sont toutes des parallélogrammes.
- L'altitude (hauteur) est la distance perpendiculaire entre les deux bases.
- Les bases sont identiques en forme et en taille.
- La section transversale parallèle aux bases a toujours la même forme et la même taille que les bases.
Quels sont des exemples concrets de prismes ?
Les prismes peuvent être trouvés dans divers objets et structures du quotidien. Les exemples comprennent:
- Prismes rectangulaires : Bâtiments, boîtes de céréales, livres.
- Prismes triangulaires : Toits de maisons, objets en forme de coin.
- Prismes pentagonaux : Certains types de colonnes, certaines structures architecturales.
- Prismes hexagonaux : Certains types de cristaux, certains contenants d'emballage.
Pourquoi la surface est-elle importante dans les prismes ?
La surface est cruciale dans les prismes car elle représente la surface totale de toutes les surfaces (faces) du prisme. Comprendre la surface aide dans diverses applications pratiques, telles que le calcul de la quantité de matériau nécessaire pour construire ou recouvrir un objet en forme de prisme, la détermination des taux de transfert de chaleur et l'optimisation de la conception de l'emballage.
