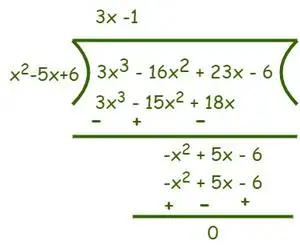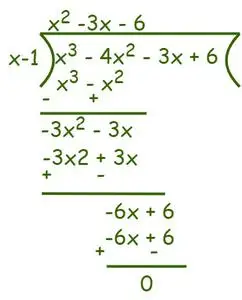Équation cubique est une équation mathématique dans laquelle un polynôme de degré 3 est assimilé à une constante ou à un autre polynôme de degré maximum 2. La représentation standard de l'équation cubique est hache ³ +bx ² +cx+d = 0 où a, b, c et d sont des nombres réels. Quelques exemples d'équation cubique sont X ³ – 4x ² + 15x – 9 = 0, 2x ³ – 4x ² = 0 etc.

Table des matières

• Définition polynomiale
• Degré d'équation
• Définition de l'équation cubique
• Comment résoudre des équations cubiques ?
• Résoudre des équations cubiques
• Résoudre l'équation cubique à l'aide de facteurs
• Résolution d'une équation cubique à l'aide de la méthode graphique
• Problèmes basés sur la résolution d'équations cubiques
• Problèmes pratiques sur la résolution d'équations cubiques

Pour apprendre à résoudre des équations cubiques, nous devons d’abord nous renseigner sur les polynômes, le degré du polynôme et autres. Dans cet article, nous découvrirons les polynômes, les équations polynomiales, la résolution d'équations cubiques ou comment résoudre des équations cubiques, et d'autres en détail.

Définition polynomiale

Le polynôme est défini comme suit,

UN polynôme est une expression algébrique dans laquelle la puissance d'une variable est un entier non négatif. La forme générale d'un polynôme est un₀Xⁿ+ un₁X^n-1+ un₂X^n-2+… + un_n. En fonction de la puissance maximale de la variable, un polynôme peut être classé en monôme, binôme, trinôme, etc.

Qu'est-ce qu'une équation ?

Une équation est définie comme suit,

Une équation est un polynôme assimilé à une valeur numérique ou à tout autre polynôme. Par exemple, x + 2 est un polynôme mais x + 2 = 5 est une équation. De même, 2x + 3 = x + 1 est également une équation alors que 2x + 3 et x + 1 sont des polynômes individuellement.

Degré d'équation

La définition du degré d’équation est indiquée ci-dessous :

Degré d'une équation est définie comme la puissance maximale possédée par la variable dans une équation.

En fonction du degré de l'équation, une équation peut être classée comme suit :

• Équation linéaire
• Équation quadratique
• Équation cubique
• Équation biquadratique

Équation linéaire

L'équation dans laquelle la puissance maximale de la variable est de 1 est appelée équation linéaire.

• Par exemple 3x +1 = 0

Polynôme quadratique

L'équation dans laquelle la puissance maximale de la variable est de 2 est une équation quadratique.

• Par exemple 3x²+x+1 = 0

Équation cubique

L'équation dans laquelle la puissance maximale de la variable est de 3 est appelée équation cubique.

programme c pour la comparaison de chaînes

• Par exemple 5x³+3x²+x+1 = 0

Polynôme biquadratique

L'équation dans laquelle la puissance maximale de la variable est de 4 est appelée polynôme biquadratique ou polynôme quartique.

• Par exemple 5x⁴+4x³+3x²+2x+1 = 0

Définition de l'équation cubique

Équation cubique est une équation algébrique où le degré le plus élevé du polynôme est 3. Quelques exemples d'équations cubiques sont 5x³+3x²+x+1 = 0,2x³+8 = x ⇒ 2x³-x+8 = 0, etc.

La forme générale d'une équation cubique est,

hache ³ + boîte ² + cx + d = 0, une ≠ 0

Où,

• un B, et c sont les coefficients de la variable et leurs exposants et d est la constante, et
• une, b, c et d sont des nombres réels.

Comment résoudre des équations cubiques ?

Une équation cubique est une équation de degré trois. Il a trois solutions et peut être résolu facilement en suivant les étapes ajoutées ci-dessous,

Étape 1: Trouvez une solution à l'équation cubique par la méthode hit and try. Supposons que nous ayons une équation cubique P(x), puis trouvons pour tout x = a, P(a) = 0 en prenant, x = 0, ±1, ±2, ±3,… et ainsi.

Étape 2: Lorsque nous obtenons P(a) = 0, trouvez le facteur (x – a) de P(x)

Étape 3: Divisez P(x) par (x – a) pour obtenir une équation quadratique, disons Q(x) en utilisant la division polynomiale.

Étape 4: Factorisez l'équation quadratique Q(x) pour obtenir les facteurs tels que (x – b) et (x – c).

Étape 5 : (x – a), (x – b) et (x – c) sont les facteurs de P(x) et en résolvant chaque facteur, nous obtenons les racines de l'équation as, a, b et c.

En savoir plus sur, Division du polynôme

Résoudre des équations cubiques

UN Équation cubique peut être résolu par deux méthodes

• En le réduisant à une équation quadratique puis en le résolvant soit par factorisation, soit par la formule quadratique
• Par méthode graphique

UN Équation cubique a trois racines. Ces racines peuvent être réelles ou imaginaires. En outre, il peut y avoir des racines distinctes ou deux racines identiques et une racine différente et les trois racines identiques.

Il convient de noter que pour toute équation, y compris Équations cubiques , l'équation doit toujours être organisée sous sa forme standard avant de résoudre l'équation.

Par exemple, si l'équation donnée est 2x²-5 = x + 4/x, alors nous devons le réorganiser sous sa forme standard, c'est-à-dire 2x³-X²-5x-4 = 0. Nous pouvons maintenant résoudre l’équation en utilisant n’importe quelle méthode appropriée.

Résoudre l'équation cubique à l'aide de facteurs

La solution de l'équation cubique à l'aide du théorème des facteurs est expliquée à l'aide de l'exemple ajouté ci-dessous,

Exemple : Trouver les racines de l'équation f(x) = 3x ³ −16x ² + 23x − 6 = 0.

Solution:

Expression donnée : f(x) = 3x³−16x²+ 23x − 6 = 0

Tout d’abord, factorisez le polynôme pour obtenir les racines

Puisque la constante est -6, les facteurs possibles sont 1, 2, 3, 6

f(1) = 3 – 16 + 23 – 6 ≠ 0

f(2) = 24 – 64 + 46 – 6 = 0

f(3) = 81 – 144 + 69 – 6 = 0

f(6) = 648 – 576 + 138 – 6 ≠ 0

Nous le savons, selon Théorème des facteurs si f(a) = 0, alors (x-a) est un facteur de f(x)

Ainsi, (x – 2) et (x – 3) sont des facteurs de f(x). Par conséquent, le produit de (x – 2) et (x – 3) sera également un facteur de f(x). Maintenant, pour trouver les facteurs restants, utilisez la méthode de division longue et divisez f(x) par le produit de (x – 2) et (x – 3)

Par conséquent, Diviseur = (x – 2)(x – 3) = (x²– 5x + 6) et Dividende = 3x³−16x²+ 23x − 6. Divisez maintenant comme indiqué ci-dessous,

Après division, nous obtenons (3x- 1) comme quotient et le reste est 0. Maintenant, selon Algorithme de division nous savons que Dividende = Diviseur × Quotient + Reste.

⇒ f(x) = (3x³−16x²+ 23x − 6) = (x²– 5x + 6)(3x-1)

Puisque f(x) = 0

⇒ (x²– 5x + 6)(3x-1) = 0

⇒x²– 5x + 6 = 0 ou 3x-1 = 0

Maintenant nous allons prendre 3x-1 = 0 ⇒ x = 1/3 car nous connaissons déjà deux racines de x²– 5x + 6 qui font 2 et 3

Donc,

Racines du donné Équation cubique sont 1/3, 2 et 3.

Résolution d'une équation cubique à l'aide d'une méthode graphique

Une équation cubique est résolue graphiquement lorsque vous ne pouvez pas résoudre l'équation donnée en utilisant d'autres techniques. Nous avons donc besoin d’un dessin précis de l’équation cubique donnée. Les racines de l'équation sont le(s) point(s) où le graphique croise l'axe X si l'équation est en termes de x et si l'équation est en termes de y alors les racines de l'équation sont les points auxquels le graphique coupe l'axe Y.

Le nombre de solutions réelles de l'équation cubique est égal au nombre de fois où le graphique de l'équation cubique croise l'axe X.

Exemple : Trouver les racines de l'équation f(x) = x ³ − 4x ² − 9x + 36 = 0, en utilisant la méthode graphique.

Solution:

Expression donnée : f(x) = x³− 4x²−9x + 36 = 0.

Maintenant, remplacez simplement x par des valeurs aléatoires dans le graphique pour la fonction donnée :

X	-4	-3	-2	-1	0	1	2	3	4	5
f(x)	-56	0	19	40	36	24	dix trouver mon iPhone Android	0	0	16

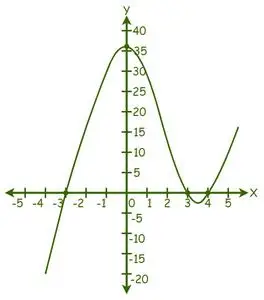
On peut voir que le graphique a coupé l'axe X en 3 points, il y a donc 3 vraies solutions.

D'après le graphique, les solutions sont : x = -3, x = 3 et x = 4.

Par conséquent, les racines de l’équation donnée sont -3, 3 et 4.

En savoir plus,

• Équation linéaire
• Résolution d'une équation quadratique
• Factorisation de polynômes

Problèmes basés sur la résolution d'équations cubiques

Problème 1 : trouver les racines de f(x) = x ³ – 4x ² -3x + 6 = 0.

Solution:

Expression donnée : f(x) = x³– 4x²-3x + 6 = 0.

Tout d’abord, factorisez le polynôme pour obtenir les racines.

Puisque la constante est +6, les facteurs possibles sont 1, 2, 3, 6.

f(1) = 1 – 4 – 3 + 6 = 7 – 7 = 0

f(2) = 8 – 16 – 6 + 6 ≠ 0

f(3) = 27 – 36 – 9 + 6 ≠ 0

f(6) = 216 – 144 -18 + 6 = -48 ≠ 0

Ainsi, selon Théorème des facteurs (x – 1) est un facteur de l’équation donnée. Maintenant, pour trouver les facteurs restants, utilisez la méthode de division longue.

Selon Algorithme de division nous pouvons écrire,

Donc, f(x) = x³– 4x²-3x + 6 = (x – 1) (x²– 3x – 6) = 0

⇒ (x – 1) = 0 ou (x²– 3x – 6) = 0

Nous savons que les racines d’une équation quadratique sont²+ bx + c = 0 sont,

x = [-b ± √(b²-4ac)]/2a

Donc pour (x²– 3x – 6) = 0

x = [3 ± √(3²– 4(1)(-6)]/2(1)

x = (3 ± √33)/2

Par conséquent, les racines de l’équation cubique donnée sont 1, (3+√33)/2 et (3–√33)/2.

Problème 2 : Trouver les racines de l'équation f(x) = 4x ³ – 10x ² + 4x = 0.

Solution:

Expression donnée : f(x) = 4x³– 10x²+ 4x = 0

⇒ x (4x²– 10x + 4) = 0

⇒ x (4x²– 8x – 2x + 4) = 0

⇒ x(4x(x – 2) – 2(x – 2)) = 0

⇒ x (4x – 2) (x – 2) = 0

réagir en style en ligne

⇒ x = 0 ou 4x – 2 = 0, x – 2 = 0

⇒ x = 0 ou x = 1/2 ou x = 2

Par conséquent, les racines de l’équation donnée sont 0, 1/2 et 2.

Problème 3 : Trouver les racines de l'équation f(x) = x ³ + 3x ² +x + 3 = 0.

Solution:

Expression donnée : f(x) = x³+ 3x²+x + 3 = 0.

⇒x²(x + 3) + 1(x + 3) = 0

⇒ (x + 3) (x²+1) = 0

⇒ x + 3 = 0 ou x²+1 = 0

⇒ x = -3, ±i

Ainsi, l’équation donnée a une racine réelle, c’est-à-dire -3, et deux racines imaginaires, c’est-à-dire ±i.

Problème 4 : Trouver les racines de l'équation f(x) = x ³ – 7x ² – x + 7 = 0.

Solution:

Des expressions données,

f(x) = x³– 3x²– 5x + 7 = 0

Tout d’abord, factorisez l’équation, f(x) : x³– 3x²– 5x + 7=0

Il peut être pris en compte dans (x-7)(x+1)(x-1) = 0

Après avoir factorisé le polynôme, nous pouvons trouver les racines en assimilant chaque facteur à zéro. Par exemple:

• x – 7 = 0, donc x = 7
• x + 1 = 0, donc x = -1
• x – 1 = 0, donc x = 1

Donc les racines de l'équation f(x) : x³– 3x²– 5x + 7 = 0 sont

• x = 7
• x = -1
• x = 1

Problème 5 : Trouver les racines de l'équation f(x) = x ³ − 6x ² + 11x − 6 = 0, en utilisant la méthode graphique.

Solution:

Expression donnée : f(x) = x³− 6x²+ 11x − 6 = 0.

Maintenant, remplacez simplement les valeurs aléatoires de x dans le graphique pour la fonction donnée :

X	1	2	3	4	5
f(x)	0	0	0	6	24 MySQL change le type de colonne

On peut voir que le graphique a coupé l'axe X en 3 points, il y a donc 3 vraies solutions.

D'après le graphique, les solutions sont : x = 1, x = 2 et x = 3.

Par conséquent, les racines de l’équation donnée sont 1, 2 et 3.

Problèmes pratiques sur la résolution d'équations cubiques

Divers problèmes pratiques liés aux équations cubiques sont ajoutés ci-dessous. Résolvez ces problèmes pour comprendre pleinement le concept de Comment résoudre une équation cubique ?

P1. Résoudre l'équation cubique, 3x³+ 2x²– 11x + 7 = 0.

P2. Trouver les racines de l'équation cubique, 4x³– 12x²+ 17 = 0.

P3. Résoudre l'équation cubique, x³+4x²– x + 3 = 0 en utilisant la méthode graphique.

P4. Trouvez le nombre qui satisfait, -9x³+ 11x²– 8x + 2 = 0.

FAQ sur la résolution d'équations cubiques

1. Que sont les équations cubiques ?

Les équations cubiques sont les équations algébriques dans lesquelles la puissance maximale d'une variable est de 3.

2. Comment factoriser une équation cubique ?

Nous pouvons factoriser une équation cubique de deux manières. Tout d’abord, en prenant une expression linéaire commune à l’équation cubique donnée, nous aurons alors une expression linéaire et quadratique comme produit. Cette équation quadratique peut être davantage factorisée pour obtenir tous les facteurs. La deuxième méthode consiste à trouver un zéro de l'équation cubique donnée en mettant des valeurs aléatoires. La valeur pour laquelle nous obtenons que la valeur de l’équation soit nulle sera l’un des zéros de l’équation cubique donnée. Maintenant, en utilisant le théorème des facteurs, formons une expression linéaire, disons x-a et divisons l'équation cubique donnée par cette expression qui donnera une équation quadratique comme quotient. Cette équation quadratique obtenue peut être davantage factorisée pour obtenir tous les facteurs.

3. Comment résoudre graphiquement une équation cubique ?

Pour résoudre graphiquement une équation cubique, mettez des valeurs aléatoires pour x dans l’équation cubique donnée et résolvez, vous obtiendrez les valeurs de y. Tracez ces valeurs obtenues sur le graphique. Trouvez les coordonnées auxquelles le graphique coupe l'axe des x. Ces coordonnées sont la solution de l'équation cubique.

4. Toutes les équations cubiques peuvent-elles être résolues exactement ?

Toute équation ayant une puissance étrange doit avoir une vraie racine. Ainsi, une équation cubique doit avoir au moins une racine réelle, contrairement à une équation quadratique où les deux racines peuvent être imaginaires lorsque le discriminant est inférieur à zéro.

5. Une équation cubique peut-elle avoir plusieurs solutions ?

Oui, les équations cubiques peuvent avoir plusieurs solutions, car une équation cubique peut avoir jusqu'à trois racines réelles distinctes.

6. Qu’entendez-vous par degré d’une équation ?

La puissance maximale possédée par la variable dans une équation est appelée degré d’un polynôme.

7. Quelle est la différence entre un polynôme et une équation ?

Le polynôme est simplement une équation algébrique dans laquelle la puissance de la variable est un entier non négatif. Ce polynôme lorsqu'il est assimilé (=) à une valeur numérique ou à un autre polynôme est alors appelé une équation.

8. Qu'est-ce que le théorème des facteurs pour les équations cubiques ?

Le théorème des facteurs stipule que si r est une racine (solution) de l'équation cubique ax³+ boîte²+ cx + d = 0, alors x – r est un facteur de l'équation.

9. Que faire si je ne parviens pas à trouver des solutions exactes à l’aide de formules ?

Si trouver des solutions exactes semble impossible, nous pouvons utiliser des méthodes numériques comme les méthodes itératives (par exemple la méthode de Newton) pour approximer les racines de l’équation.

En savoir plus sur La méthode de Newton Raphson .