Il existe de nombreuses façons d'évaluer les performances d'un classificateur. Dans cet article, nous présentons la courbe de rappel de précision et examinons plus en détail la différence entre deux méthodes courantes de reporting des performances : la courbe de rappel de précision (PR) et Caractéristiques de fonctionnement du récepteur (ROC) Courbe. La courbe ROC est déjà discutée dans le article . Comprenons brièvement ce qu'est une courbe Précision-Rappel.
Qu'est-ce que la précision et le rappel ?
Précision
- Le rapport entre les observations positives correctement prédites et tous les positifs prédits est appelé précision.
- Il évalue dans quelle mesure le modèle prévoit les résultats positifs.
- La formule de précision est :
- La précision concerne la qualité des prédictions positives. Une précision élevée indique que le modèle présente un faible taux de faux positifs.
Rappel
- Le rapport entre les observations positives correctement prédites et le nombre total d’observations positives réelles est appelé rappel.
- Il évalue dans quelle mesure le modèle peut capturer chaque instance pertinente.
- Le rappel est calculé à l'aide de cette formule :
- Le rappel concerne la quantité d'instances pertinentes capturées par le modèle. Un rappel élevé indique que le modèle a un faible taux de faux négatifs.
En termes d’interprétation empirique, une matrice de confusion comprenant quatre termes essentiels est l’outil le plus utile pour comprendre la précision et le rappel :
- True Positive (TP) : nombre d'instances de classe positives identifiées avec précision
- Faux positif (FP) : le nombre d'instances de classe négatives identifiées par erreur comme des instances de classe positives est appelé faux positif (FP).
- True Negative (TN) : nombre d'instances de classe négatives identifiées avec précision
- Faux négatif (FN) : nombre d'instances de classe positives classées par erreur comme instances de classe négatives (faux négatif ou FN)
Courbe de rappel de précision (PR) dans l'apprentissage automatique
Précision est la proportion de correct classifications positives (vrai positif) divisé par le nombre total de prédit classifications positives qui ont été faites (vrai positif + faux positif). Rappel est la proportion de correct classifications positives (vrai positif) divisé par le nombre total de vraiment classifications positives (vrai positif + faux négatif).
Une courbe PR est simplement un graphique avec des valeurs de précision sur l'axe des y et des valeurs de rappel sur l'axe des x. En d’autres termes, la courbe PR contient
- Il est important de noter que la précision est également appelée valeur prédictive positive (VPP).
- Le rappel est également appelé sensibilité, taux de réussite ou taux de vrais positifs (TPR).
La figure ci-dessous montre une comparaison d’exemples de courbes PR et ROC. 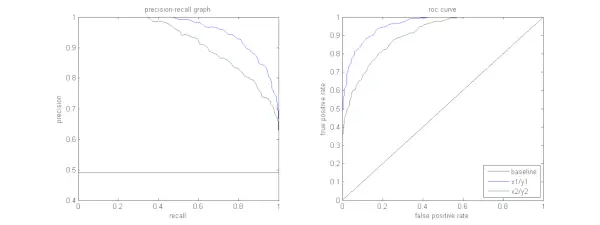
Interprétation d'une courbe de rappel de précision
Il est souhaité que l'algorithme ait à la fois une haute précision et un haut rappel. Cependant, la plupart des algorithmes d’apprentissage automatique impliquent souvent un compromis entre les deux. Une bonne courbe PR a une plus grande AUC (aire sous la courbe) . Dans la figure ci-dessus, le classificateur correspondant à la ligne bleue a de meilleures performances que le classificateur correspondant à la ligne verte. Il est important de noter que le classificateur qui a une AUC plus élevée sur le Courbe ROC aura toujours également une AUC plus élevée sur la courbe PR. Considérons un algorithme qui classe si un document appartient ou non à la catégorie Actualités sportives. Supposons qu’il existe 12 documents, avec les étiquettes de vérité terrain (réelles) et de classe de sortie du classificateur suivantes.
java synchroniser
| ID du document | Vérité terrain | Sortie du classificateur |
|---|---|---|
| D1 | Des sports | Des sports |
| D2 | Des sports | Des sports |
| D3 | Pas de sport | Des sports |
| D4 | Des sports | Pas de sport |
| D5 | Pas de sport | Pas de sport |
| D6 | Des sports | Pas de sport |
| J7 | Pas de sport | Des sports |
| D8 | Pas de sport | Pas de sport |
| D9 | Pas de sport | Pas de sport |
| J10 | Des sports | Des sports |
| J11 | Des sports | Des sports |
| J12 | Des sports | Pas de sport |
Maintenant, trouvons les valeurs TP, TN, FP et FN.
Utilisons un exemple impliquant des documents classés comme Sports ou Non sportifs pour mieux expliquer les définitions des vrais positifs (TP), des vrais négatifs (TN), des faux positifs (FP) et des faux négatifs (FN) dans le contexte de la classification :
Vrais positifs (TP) : Des documents qui étaient précisément classés comme sports et qui concernaient en fait le sport. Les documents D1, D2, D10 et D11 dans ce scénario sont des instances de TP.
Vrais négatifs (TN) : Les vrais négatifs sont les cas dans lesquels le document a été étiqueté à juste titre comme non sportif même s'il n'avait rien à voir avec le sport. Dans le cas présent, le TN est démontré par les documents D5, D8 et D9.
Faux positifs (FP) : Des documents classés par erreur comme Sports alors qu’ils n’avaient rien à voir avec le sport. Voici quelques exemples de FP, documents D3 et D7.
Faux négatifs (FN) : Exemples de documents qui ont été étiquetés par erreur comme n'étant pas du sport, alors qu'en réalité, ils concernaient le sport. Les documents D4, D6 et D12 sont dans ce cas des exemples FN.
Compte tenu de ces chiffres : Ville =4, TN =3, FP =2, FR =3
Enfin, la précision et le rappel sont calculés comme suit :
Precision = frac{TP}{TP+FP} = frac{4}{6} = frac{2}{3}
Recall = frac{TP}{TP+FN} = frac{4}{7} Il s'ensuit que le rappel est de 4/7 lorsque la précision est de 2/3. En d’autres termes, parmi tous les cas qui étaient censés être positifs, les deux tiers ont été classés avec précision (précision), et parmi tous les cas réellement positifs, le modèle a pu en capturer quatre septièmes (rappel).
En définissant différents seuils, nous obtenons plusieurs paires de précision et de rappel. En traçant plusieurs de ces paires P-R avec l'une ou l'autre valeur allant de 0 à 1, nous obtenons une courbe PR.
Besoin d’une courbe PR alors que la courbe ROC existe ?
La courbe PR est particulièrement utile pour rapporter les résultats de la recherche d'informations.
La recherche d'informations consiste à rechercher dans un pool de documents ceux qui sont pertinents pour une requête utilisateur particulière. Par exemple, supposons que l’utilisateur saisisse une requête de recherche Pink Elephants. Le moteur de recherche parcourt des millions de documents (à l’aide d’algorithmes optimisés) pour récupérer une poignée de documents pertinents. Par conséquent, nous pouvons supposer avec certitude que le non. de documents pertinents sera bien moindre par rapport au non. de documents non pertinents.
tableau dynamique en Java
Dans ce scénario,
- TP = Nombre de documents récupérés pertinents (bons résultats).
- FP = Nombre de documents récupérés qui ne sont pas pertinents (faux résultats de recherche).
- TN = Nombre de documents non récupérés et non pertinents.
- FN = Nombre de documents pertinents non récupérés (bons documents que nous avons manqués).
La courbe ROC est un tracé contenant Recall = TPR =
De plus, FPR ne nous aide pas à bien évaluer un système de récupération car nous souhaitons nous concentrer davantage sur les documents récupérés, et non sur ceux non récupérés. La courbe PR aide à résoudre ce problème. La courbe PR a la valeur de rappel (TPR) sur l'axe des x et la précision =
Quand utiliser les courbes ROC par rapport aux courbes de rappel de précision ?
ROC (Receiver Operating Characteristic) conviennent lorsque la distribution des classes est équilibrée et que les faux positifs et les faux négatifs ont des conséquences similaires. Ils illustrent le compromis entre sensibilité et spécificité. En revanche, les courbes Précision-Rappel sont préférables lorsqu'il s'agit d'ensembles de données déséquilibrés, en se concentrant sur les performances de prédiction de classe positive.
Precision-Recall fournit des informations sur la capacité du modèle à classer correctement les instances positives. Le choix entre ROC et Precision-Recall dépend des besoins spécifiques du problème, soulignant l'importance de comprendre la distribution des données et les conséquences des différents types d'erreurs.
Implémentation de code de base pour la courbe de rappel de précision
Importation des bibliothèques nécessaires
Ces lignes de code importent le Bibliothèques Python et les modules nécessaires pour générer une courbe de précision-rappel avec science-kit-apprendre et visualisez les résultats avec Matplotlib . Matplotlib est une bibliothèque de traçage Python populaire et pyplot fournit une interface simple pour créer différents types de tracés et de graphiques. Régression logistique est un algorithme de classification populaire pour les tâches de classification binaire et multiclasse. La courbe précision-rappel et l'AUC sont des mesures d'évaluation populaires pour classification binaire problèmes, en particulier lorsqu’il s’agit d’ensembles de données déséquilibrés.
Python3 import matplotlib.pyplot as plt from sklearn.datasets import make_classification from sklearn.model_selection import train_test_split from sklearn.linear_model import LogisticRegression from sklearn.metrics import precision_recall_curve, auc> Ensemble de données utilisé
Ce code génère un ensemble de données synthétiques pour un problème de classification binaire à l'aide de la fonction « make_classification » de sci-kit-learn.
Python3 # Generate a synthetic dataset X, y = make_classification( n_samples=1000, n_features=20, n_classes=2, random_state=42)> Séparation d'entraînement et de test
Le train_test_split La fonction dans scikit-learn est utilisée dans cet extrait de code pour diviser l'ensemble de données synthétiques précédemment généré (X et y) en ensembles d'entraînement et de test. Cette division est une étape critique dans l’évaluation des modèles d’apprentissage automatique. Le modèle sera entraîné sur les données X_train et y_train avant d'être testé sur les données X_test et y_test pour voir ses performances sur des échantillons invisibles. La fonction train_test_split sépare les ensembles de formation et de test, garantissant que les performances du modèle reflètent sa généralisation à de nouvelles données inédites.
Python3 # Split the dataset into training and testing sets X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.2, random_state=42)> Construction de modèles
Ici, nous utilisons la régression logistique pour entraîner le modèle sur l'ensemble de données d'entraînement. Algorithme populaire pour la classification binaire, la régression logistique est implémentée par la classe sci-kit-learn LogisticRegression.
Python3 # Train a logistic regression model (you can replace this with your own classifier) model = LogisticRegression() model.fit(X_train, y_train)> Prédiction du modèle
Ces calculs donnent généralement des valeurs de précision et de rappel pour différents seuils de décision, que vous pouvez utiliser pour tracer une courbe précision-rappel ou examiner l'importance relative de la précision et du rappel à différents moments. Et en calculant le Aire sous la courbe (AUC) pour la courbe précision-rappel.
Python3 # Predict probabilities for positive class y_scores = model.predict_proba(X_test)[:, 1] # Calculate precision and recall precision, recall, thresholds = precision_recall_curve(y_test, y_scores) # Calculate Area Under the Curve (AUC) for precision-recall curve auc_score = auc(recall, precision)> Tracer la courbe PR
Ce bloc de code fournit une méthode standard pour visualiser la courbe précision-rappel et vous permet d'évaluer le compromis précision/rappel à différents seuils de décision. Les performances globales du modèle sur la courbe précision-rappel sont résumées par le score AUC indiqué dans la légende.
Python3 # Plot precision-recall curve plt.figure(figsize=(8, 6)) plt.plot(recall, precision, label=f'Precision-Recall Curve (AUC = {auc_score:.2f})') plt.xlabel('Recall') plt.ylabel('Precision') plt.title('Precision-Recall Curve') plt.legend() plt.show()> Sortir :

Courbe précision-rappel
Foire aux questions (FAQ)
Q. Qu'est-ce que la précision ?
Le rapport entre les observations positives prédites avec précision et le nombre total de positifs prédits est appelé précision. Il évalue dans quelle mesure le modèle prédit les résultats positifs. Voici la formule de précision :
Precision = frac{True Positives}{True Positives + False Positives}
Q. Qu'est-ce que le rappel ?
Le rappel est le rapport entre les observations positives correctement prédites et le nombre total de positifs réels. On l’appelle également sensibilité ou taux de vrais positifs. Il évalue dans quelle mesure le modèle peut capturer chaque instance pertinente. Le rappel est calculé à l'aide de la formule suivante :
Precision = frac{True Positives}{True Positives + False Negatives}
Q. Pourquoi avons-nous besoin de précision et de rappel ?
Pour évaluer les performances d'un classificateur dans les problèmes de classification binaire et multiclasse, deux métriques d'évaluation sont utilisées : la précision et le rappel. L'exactitude des prédictions positives est mesurée par la précision, et l'exhaustivité des prédictions positives est mesurée par le rappel.
Q. Quel est le compromis entre rappel et précision ?
Le rappel et la précision sont souvent des compromis. Le rappel peut souffrir à mesure que la précision augmente, et vice versa. En modifiant la barre d'identification d'une instance positive, ce compromis peut être géré. À l’inverse, un seuil inférieur entraîne un rappel plus faible mais une précision plus élevée. La décision entre rappel et précision est basée sur les particularités du problème donné.
Q. Qu'est-ce que le score F1 et quel est son rapport avec la précision et le rappel ?
La moyenne harmonique de rappel et de précision est connue sous le nom de score F1. Il offre une mesure juste qui prend en compte à la fois les faux positifs et les faux négatifs. Le score F1 est calculé selon la formule suivante :
F1-Score = frac{2 imes Precision imes Recall}{Precision + Recall} Le score F1 est particulièrement utile lorsque la précision et le rappel sont déséquilibrés et qu’un équilibre entre les deux est souhaité.
table de hachage java
