Moins que signe, noté <, est un symbole mathématique qui montre une inégalité entre deux valeurs. Lorsque nous utilisons le symbole <, cela signifie que la valeur ou la quantité du côté gauche est inférieure à la valeur du côté droit.
Discutons Moins que le symbole , ses applications dans les inégalités ainsi que quelques exemples résolus.
Table des matières
- Qu'est-ce que le symbole inférieur au symbole ?
- Exemples de symboles inférieurs à
- Tableau des signes mathématiques – Inférieur à, supérieur à et égal à
- Comment se souvenir de moins que le symbole ?
- Symboles inférieur, supérieur et égal à
- Moins que le symbole dans les inégalités
- Questions inférieures au symbole
Qu'est-ce que le symbole inférieur au symbole ?
Le signe inférieur (<) est un symbole utilisé entre deux valeurs, ce qui signifie que la valeur de gauche est plus petite que la valeur de droite.
- Le symbole < indique plus petit que.
- Symbole inférieur à, noté (<) , est utilisé pour représenter la relation entre deux nombres ou quantités.
- Le symbole inférieur à est binaire, ce qui signifie qu'il nécessite deux opérandes et est lu comme moins que ou plus petit que.
Inférieur à la signification du symbole
Le symbole inférieur à (<) est utilisé en mathématiques pour indiquer que la valeur du côté gauche du symbole est inférieure à la valeur du côté droit. Par exemple, dans l’expression 3<53<5, il est indiqué que 3 est inférieur à 5.
Exemples de symboles inférieurs à
Voici quelques exemples de symbole inférieur à :
- 3 <5 (Trois est inférieur à cinq)
- -2 <0 (moins deux est inférieur à zéro)
- 7 <7 (Sept n'est pas inférieur à sept. Il est égal à sept)
Tableau des signes mathématiques – Inférieur à, supérieur à et égal à
Le tableau suivant représente les signes mathématiques à des fins de comparaison ainsi que leur nom, leur signification et des exemples.
| Signes mathématiques – Signification et exemples | |||
|---|---|---|---|
| Symbole/Signe | < | = | > |
| Nom | moins que | est égal à | plus grand que |
| Indique | la valeur de gauche est inférieure à celle de droite | les valeurs gauche et droite sont égales | la valeur de gauche est supérieure à la valeur de droite |
| Exemple | 5 <7 | 5 = 5 | 7> 5 |
Comment se souvenir de moins que le symbole ?
Le signe moins que et son homologue supérieur à ont une représentation visuelle presque similaire mais dans la direction opposée. Par conséquent, pour éviter toute confusion, il existe deux astuces grâce auxquelles nous pouvons nous rappeler quel est le signe de Less Than.
Ces méthodes sont appelées Méthode L et Méthode avec une bouche plus petite.
Méthode L pour le symbole inférieur à
Cette méthode est simple – moins que commence par une lettre L, donc le symbole qui ressemble le plus à un L est celui qui signifie moins que .
Bouche fermée Méthode pour le symbole inférieur à
La bouche fermée sur le côté gauche indique moins que le symbole. L'extrémité fermée de < pointe vers la plus petite quantité.

Symboles inférieur, supérieur et égal à
Nous allons maintenant discuter brièvement de Supérieur à, Inférieur à, Égal à Signer.
- Signe supérieur à
- Moins que le signe
- Égal au signe
Signe supérieur à
Signe supérieur à > est utilisé pour exprimer un type spécifique de comparaison entre deux quantités, où la valeur de gauche est supérieure à la valeur de droite.
Exemple : 10> 5 ; (dix est supérieur à cinq)
Moins que le signe
Moins que le signe < est utilisé pour exprimer un type spécifique de comparaison entre deux quantités, où la valeur de gauche est inférieure à la valeur de droite.
Exemple : 5 <10 ; (cinq est inférieur à 10)
Égal au signe
Égal au signe = est utilisé pour montrer l’égalité entre deux nombres ou valeurs. Il exprime que les valeurs de gauche et de droite sont égales.
Exemple : 5 + 5 = 10 soit 10 = 10 (dix est égal à dix)
Ci-dessus se trouvent les signes fondamentaux qui sont utilisés à des fins de comparaison, il existe d'autres signes qui sont formés par une combinaison de signes. Ceux-ci sont supérieur à égal à et inférieur à égal à.
Inférieur ou égal au symbole
Inférieur ou égal au symbole ≤ est utilisé lorsqu'il existe une ambiguïté entre l'ampleur de la quantité. Disons que nous avons une déclaration qui indique que le nombre de pommes que possède Ram est inférieur ou égal à celui de Rohan. Ensuite, nous pouvons l'exprimer mathématiquement comme x ≤ y où x est le nombre de pommes avec Ram et y est le nombre de pommes avec Rohan.
Pas moins que le symbole
Pas moins que le symbole ≮ est utilisé lorsque la quantité sur le côté gauche n’est pas inférieure à la quantité sur le côté droit. Cela signifie que la quantité du côté gauche est égale ou supérieure à la quantité du côté droit.
Disons que l’âge de Jean est de « p » ans et qu’Andrew a « q » ans et que l’âge de John n’est pas inférieur à celui d’Andrew. Cela signifie que l’âge de Jean est égal ou supérieur à celui d’Andrew. Nous pouvons l’exprimer mathématiquement comme p ≮ q.
Lire en détail : Symboles supérieur et inférieur à
Moins que le symbole dans les inégalités
Une inégalité est une déclaration qui compare deux expressions, et le symbole inférieur à indique que l'expression de gauche est plus petite que celle de droite. Le symbole inférieur à est fréquemment utilisé dans les inégalités mathématiques
Types d'inégalités
Les inégalités sont de deux types nommés ainsi,
- Inégalités strictes
- Inégalités non strictes
Ces deux inégalités sont discutées ci-dessous :
Inégalité stricte (<)
Ce type d’inégalité représente une situation où le membre de gauche est strictement plus petit que le membre de droite.
Par exemple:
- 2 <7
- x <10 ; x est inférieur à 10, cela signifie que x peut être compris entre -∞ et 9
Inégalité stricte sur la droite numérique
Pour visualiser les inégalités à l’aide du symbole inférieur à, vous pouvez tracer les nombres sur une droite numérique. La droite numérique fournit une représentation graphique de la façon dont les valeurs se comparent les unes aux autres.
Prenons un exemple :
x <4. Cette inégalité signifie que la valeur de x est inférieure à 4. Sur la droite numérique, vous représenteriez cela en ombrant la région à gauche de 4.

Inégalités non strictes (≤)
Dans ce cas, le côté gauche peut être plus petit mais peut également être égal au côté droit.
Par exemple : 3 ≤ 3 (Trois est inférieur ou égal à trois).
Inégalité non stricte sur la droite numérique
Prenons un exemple :
x ≤ 4, cette inégalité signifie que la valeur de x est inférieure ou égale à 4 (dont 4). Sur la droite numérique, vous représenteriez cela en ombrant la région à gauche et sur le 4.

Exemples de symboles inférieurs à
Ici, nous avons résolu quelques exemples de questions à apprendre.
Exemple 1 : Comment représenter symboliquement 10 est inférieur à 50 ?
Solution:
10 est inférieur à 50 est symboliquement représenté comme 10 <50
Exemple 2 : Déterminez si les affirmations suivantes sont vraies ou fausses :
un) 8 <12
b) -5 <-7
c) 6 <6
Solution:
une véritable (8 est inférieur à 12)
b) Faux (-5 n'est pas inférieur à -7)
c) Faux (6 n'est pas inférieur à 6 ; ils sont égaux)
Exemple 3 : Trouver le nombre entier possible pour 'x' ; où 10
Solution:
Étant donné, 10
À partir de 10
De x <15 , x peut être : (-∞….. 9, 10, 11, 12, 13, 14, 15)
En prenant la distance entre les deux, l'énoncé que nous obtenons x peut être : 11, 12, 13, 14, 15, 16
Exemple 4 : Résoudre pour x : 3x <15
Solution:
Pour trouver la valeur de x, divisez les deux côtés de l’inégalité par 3 :
3x <15
x <15 / 3
x <5
Donc la solution est x <5
Exemple 5 : Un jardin rectangulaire mesure 12 pieds de long et 8 pieds de large. Un autre jardin rectangulaire mesure 15 pieds de long et 10 pieds de large. Quel jardin a une plus petite superficie ?
Solution:
Pour comparer les superficies, calculez les superficies des deux jardins
programme en javaLe premier jardin a une superficie de 12 pieds × 8 pieds = 96 pieds carrés
Le deuxième jardin a une superficie de 15 pieds × 10 pieds = 150 pieds carrés
Nous le savons, 96 <150
Le premier jardin a une superficie plus petite car 96 est inférieur à 150
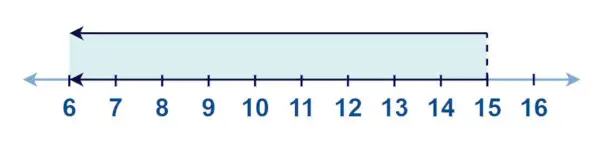
Exemple 6 : Pour x <15 , dessinez x sur la droite numérique.
Solution:
Sur la droite numérique x <15 est dessiné comme :

Questions inférieures au symbole
Voici quelques questions sur Less Than Sign pour votre pratique.
T1. Ram a 5 caramels et Shyam a 8 caramels. Qui a moins de caramels ?
Q2. Bob dort 1/2 heure et Alice 60 minutes chaque jour l'après-midi. Qui dort moins de temps ?
Q3. Indiquez si la déclaration donnée est vraie ou fausse :
- 5 <8
- 10 <7
- x <100 ; où x = 20
Q4. Trouvez le nombre entier possible pour ' x ' ; où 5
Q5. Dessinez ' x ' sur la droite numérique ; où x <100.
Q6. Placez le symbole Supérieur ou Inférieur à Tham dans ce qui suit
- 2__5
- 0,25 __ 0,252
- -14 __ 0
- 1/4 __ 1/3
Les gens lisent également :
- Symboles supérieur et inférieur à
- Signe égal
- Plus qu'un signe
FAQ sur le symbole inférieur à
Que représente Moins que le signe en mathématiques ?
Le signe inférieur à (<) est un symbole mathématique utilisé pour indiquer que la valeur de gauche est plus petite ou d'une ampleur inférieure à la valeur de droite.
Quel est l'opposé du symbole inférieur au symbole ?
L’opposé du symbole inférieur à (), qui indique qu’une valeur est supérieure à l’autre.
À quoi ressemble le symbole « moins que » ?
Le symbole inférieur à ressemble à un « L » incliné. Veuillez vous référer à l'image dans l'article.
Quelle est l’utilisation du signe « moins que » ?
Le signe inférieur à (<) est utilisé pour indiquer qu’une valeur est inférieure à une autre. Par exemple, dans l’énoncé 3 < 5, cela signifie que 3 est inférieur à 5.
Quelle est la différence entre les symboles supérieur à, inférieur à et égal à ?
Le symbole supérieur à (>) indique que la valeur de gauche est supérieure à la valeur de droite, tandis que le symbole inférieur à (<) indique que la valeur de gauche est inférieure à la valeur de droite. Le symbole égal à (=) indique que les valeurs des deux côtés sont exactement les mêmes.
Le symbole inférieur à peut-il être utilisé avec des variables ?
Oui, le symbole inférieur à peut être utilisé dans les inégalités impliquant des variables. Par exemple, x <10 signifie que la variable x est inférieure à 10.
Quelle est la différence entre les inégalités strictes et non strictes ?
Dans une inégalité stricte (par exemple, x <5), la valeur de gauche doit être strictement inférieure à la valeur de droite. Dans une inégalité non stricte (par exemple, x ≤ 5), la valeur de gauche peut être égale à la valeur de droite.
