La valeur arithmétique utilisée pour représenter la quantité et utilisée dans les calculs est définie comme des nombres. Un symbole comme 4, 5, 6 qui représente un nombre est appelé chiffre. Sans chiffres, nous ne pouvons pas compter les choses, la date, l’heure, l’argent, etc., ces chiffres sont également utilisés pour la mesure et pour l’étiquetage.

Les propriétés des nombres les rendent utiles pour effectuer des opérations arithmétiques sur eux. Ces nombres peuvent être écrits sous forme numérique et également sous forme de mots.

Par exemple , 3 s'écrit trois en mots, 35 s'écrit trente-cinq en mots, etc. Les élèves peuvent écrire les nombres de 1 à 100 en mots pour en savoir plus.

Il existe différents types de nombres que nous pouvons apprendre. Ce sont des nombres entiers et naturels, des nombres pairs et impairs, des nombres rationnels et irrationnels, etc.

Qu'est-ce qu'un système numérique ?

Un système numérique est une méthode d'affichage des nombres par écriture, qui est une manière mathématique de représenter les nombres d'un ensemble donné, en utilisant les nombres ou les symboles de manière mathématique. Le système d'écriture permettant de désigner des nombres à l'aide de chiffres ou de symboles de manière logique est défini comme le système numérique.

On peut utiliser les chiffres de 0 à 9 pour former tous les nombres. Avec ces chiffres, n’importe qui peut créer des nombres infinis.

Par exemple, 156, 3907, 3456, 1298, 784859, etc.

Qu'est-ce qu'une racine carrée ?

La valeur d'un nombre de racines carrées qui, lors de la multiplication par elle-même, donne le nombre d'origine. Supposons que a soit la racine carrée de b, alors elle est représentée par a = √b ou nous pouvons exprimer la même équation que a2 = b. Ici, «√», ce symbole que nous avons utilisé pour représenter la racine des nombres, est qualifié de radical. Le nombre positif lorsqu'il doit être multiplié par lui-même représente le carré du nombre. La racine carrée du carré de tout nombre positif donne le nombre original.

Par exemple, le carré de 4 est 16, 4²= 16, et la racine carrée de 16, √16 = 4. Puisque 4 est un carré parfait, il est donc facile de trouver la racine carrée de tels nombres, mais pour un carré imparfait, c'est vraiment délicat.

La racine carrée est représentée par '√' C'est ce qu'on appelle un symbole radical. Pour représenter un nombre « a » sous forme de racine carrée en utilisant ce symbole, vous pouvez écrire : « √a », où a est le nombre.

bash vérifie si la variable d'environnement est définie

Le nombre ici sous le symbole radical s’appelle le radicand. Par exemple, la racine carrée de 4 est également représentée comme un radical de 4. Les deux représentent la même valeur.

La formule pour trouver la racine carrée est : une = √b

Propriétés des racines carrées

Il est défini comme une fonction un-à-un qui prend un nombre positif comme entrée et renvoie la racine carrée du nombre d'entrée donné.

f(x) = √x

Par exemple, ici, si x = 9, alors la fonction renvoie la valeur de sortie 3.

Les propriétés de la racine carrée sont les suivantes :

la chaîne Java est vide

• Si un nombre est un carré parfait, alors il existe certainement une racine carrée parfaite.
• Si un nombre se termine par un nombre pair de zéros (0), alors nous pouvons avoir une racine carrée.
• Les deux valeurs de racine carrée peuvent être multipliées. Par exemple, √3 peut être multiplié par √2, le résultat sera alors √6.
• Lorsque deux mêmes racines carrées sont multipliées, le résultat doit être un nombre radical. Cela montre que le résultat est un nombre non racine carrée. Par exemple, lorsque √7 est multiplié par √7, le résultat obtenu est 7.
• La racine carrée des nombres négatifs n'est pas définie. Le carré parfait ne peut donc pas être négatif.
• Certains nombres se terminent par 2, 3, 7 ou 8 (dans le chiffre unitaire), alors la racine carrée parfaite n'existe pas.
• Certains nombres se terminent par 1, 4, 5, 6 ou 9 dans le chiffre de l'unité, le nombre aura alors une racine carrée.

Il est facile de trouver la racine carrée d’un nombre qui est un carré parfait.

Carrés parfaits sont ces nombres positifs qui peuvent être écrits comme la multiplication d'un nombre par lui-même, ou vous pouvez dire qu'un carré parfait est un nombre qui est la valeur de puissance 2 de n'importe quel entier.

Nombre qui peut être exprimé comme le produit de deux nombres entiers égaux. Par exemple, 16 est un carré parfait car il est le produit de deux nombres entiers égaux, 4 × 4 = 16. Cependant, 24 n'est pas un carré parfait car il ne peut pas être exprimé comme le produit de deux nombres entiers égaux. (8 × 3 = 24).

Le nombre obtenu en mettant au carré un nombre entier est appelé carré parfait.

Si nous supposons que N est un carré parfait d'un nombre entier y, cela peut s'écrire N = le produit de y et y = y².

Ainsi, la formule du carré parfait peut s’exprimer comme suit :

N = Oui ²

Utilisons la formule avec des valeurs :

Si y = 9 et N = y²

Cela signifie, N = 9²= 81.

Ici, 81 est un carré parfait de 9 car c'est le carré d'un nombre entier.

j e s t

À l’aide des racines carrées, nous pouvons identifier si un nombre est un carré parfait ou non, si nous calculons la racine carrée du nombre donné.

Si la racine carrée est un nombre entier, alors le nombre donné sera un carré parfait, et si la valeur de la racine carrée n'est pas un nombre entier, alors le nombre donné n'est pas un carré parfait.

Par exemple, pour vérifier si 24 est un carré parfait ou non, on va calculer sa racine carrée. √24 = 4,898979. Comme nous pouvons le voir, 4,898979 n’est pas un nombre entier, donc 24 n’est pas un carré parfait.

Prenons un autre exemple de

Le nombre 49. √49 = 7. On voit que 7 est un nombre entier, donc 49 est un carré parfait.

196 est-il un carré parfait ?

Solution:

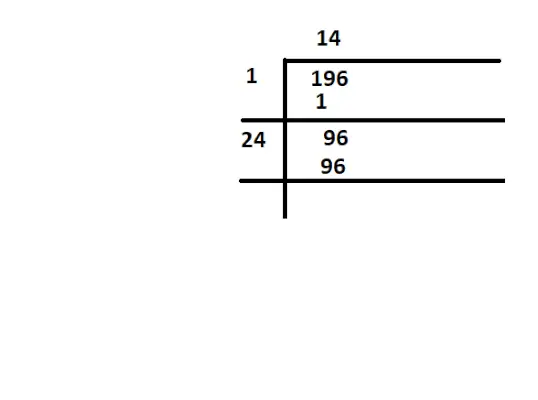
Pour vérifier si 196 est un carré parfait, il faut trouver les racines carrées de 196

carré parfait de 196

méthode tostring

Ici la racine carrée de 196 est 14

Les carrés parfaits sont ces nombres positifs qui peuvent être écrits comme la multiplication d'un nombre par lui-même, ou vous pouvez dire qu'un carré parfait est un nombre qui est la valeur de puissance 2 de n'importe quel nombre entier.

Ici on peut écrire √196 = 14 ou 14²= 14 × 14 = 196.

Donc 196 est un carré parfait.

Questions similaires

Question 1 : Quelle est la racine carrée de 625 ?

Solution:

carré parfait de 625

commandes sql ddl

ici 625 est un carré parfait de 25

On peut donc écrire √625 = 25 ou 25²= 25 × 25 = 625

Question 2 : Comment trouve-t-on la racine carrée de 24 ?

Solution:

racine carrée de 24

Ici, 24 n'est pas un carré parfait de 4,8989.

Donc √24 = 4,8989..

Question 3 : Trouver la racine carrée de 361 ?

Solution:

carré de 361

Ici la racine carrée de 361 est 19 , un nombre entier qui est un carré parfait

Donc √361 = 19 ou 19²= 19 × 19 = 361