Finite Automata(FA) est la machine la plus simple pour reconnaître des modèles. Elle est utilisée pour caractériser un langage régulier, par exemple : /baa+!/.
Il est également utilisé pour analyser et reconnaître les expressions du langage naturel. Les automates finis ou machine à états finis sont une machine abstraite qui comporte cinq éléments ou tuples. Il comporte un ensemble d'états et de règles pour passer d'un état à un autre, mais cela dépend du symbole d'entrée appliqué. En fonction des états et de l'ensemble de règles, la chaîne d'entrée peut être acceptée ou rejetée. Fondamentalement, il s'agit d'un modèle abstrait d'ordinateur numérique qui lit une chaîne d'entrée et modifie son état interne en fonction du symbole d'entrée actuel. Chaque automate définit un langage, c'est-à-dire un ensemble de chaînes qu'il accepte. La figure suivante montre quelques fonctionnalités essentielles de l’automatisation générale.
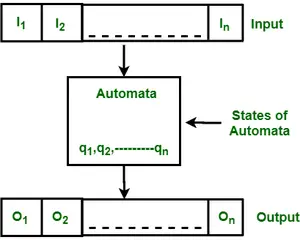
Chiffre: Caractéristiques des automates finis
La figure ci-dessus montre les caractéristiques suivantes des automates :
- Saisir
- Sortir
- États des automates
- Relation d'État
- Relation de sortie
Un automate fini se compose des éléments suivants :
Q : Finite set of states. ? : set of Input Symbols. q : Initial state. F : set of Final States. ? : Transition Function.>
La spécification formelle de la machine est
lexicographiquement
{ Q, ?, q, F, ? }> FA se caractérise en deux types :
1) Automates finis déterministes (DFA) :
DFA consists of 5 tuples {Q, ?, q, F, ?}. Q : set of all states. ? : set of input symbols. ( Symbols which machine takes as input ) q : Initial state. ( Starting state of a machine ) F : set of final state. ? : Transition Function, defined as ? : Q X ? -->Q.> Dans un DFA, pour un caractère de saisie particulier, la machine passe à un seul état. Une fonction de transition est définie sur chaque état pour chaque symbole d'entrée. De plus, dans DFA, le déplacement nul (ou ?) n'est pas autorisé, c'est-à-dire que DFA ne peut pas changer d'état sans aucun caractère d'entrée.
Par exemple, construisez un DFA qui accepte un langage de toutes les chaînes se terminant par « a ».
Donné: ? = {une,b}, q = {q0}, F={q1}, Q = {q0, q1}
Tout d’abord, considérons un ensemble de langage de toutes les chaînes acceptables possibles afin de construire un diagramme de transition d’état précis.
L = {a, aa, aaa, aaaa, aaaaa, ba, bba, bbba, père, père, père, père}
Ci-dessus se trouve un simple sous-ensemble des chaînes acceptables possibles. Il peut y avoir de nombreuses autres chaînes se terminant par « a » et contenant des symboles {a,b}.
collections en java
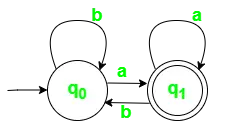
Fig 1. Diagramme de transition d'état pour DFA avec ? = {une, b}
Les chaînes non acceptées sont,
ab, bb, aab, abbb, etc.
Table de transition d'état pour l'automate ci-dessus,
| ?ÉtatSymbole? | un | b |
|---|---|---|
| q0 | q1 | q0 |
| q1 | q1 | q0 |
Une chose importante à noter est, il peut y avoir plusieurs DFA possibles pour un modèle . Un DFA avec un nombre minimum d’états est généralement préféré.
2) Automates finis non déterministes (NFA) : NFA est similaire à DFA, à l'exception des fonctionnalités supplémentaires suivantes :
- Un mouvement nul (ou ?) est autorisé, c'est-à-dire qu'il peut avancer sans lire de symboles.
- Possibilité de transmettre à n'importe quel nombre d'états pour une entrée particulière.
Cependant, ces fonctionnalités ci-dessus n’ajoutent aucune puissance à NFA. Si l’on compare les deux en termes de puissance, les deux sont équivalents.
En raison des fonctionnalités supplémentaires ci-dessus, NFA a une fonction de transition différente, le reste est identique à DFA.
?: Transition Function ?: Q X (? U ? ) -->2 ^ Q.>
Comme vous pouvez le voir dans la fonction de transition pour toute entrée incluant null (ou ?), NFA peut accéder à n'importe quel nombre d'états. Par exemple, vous trouverez ci-dessous un NFA pour le problème ci-dessus.
comment ouvrir un fichier en java
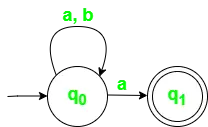
Fig 2. Diagramme de transition d'état pour NFA avec ? = {une, b}
Table de transition d'état pour l'automate ci-dessus,
| ?ÉtatSymbole? | un | b |
|---|---|---|
| q0 | {q0,q1} | q0 |
| q1 | ? | ? |
Une chose importante à noter est, dans NFA, si un chemin pour une chaîne d'entrée mène à un état final, alors la chaîne d'entrée est accepté . Par exemple, dans le NFA ci-dessus, il existe plusieurs chemins pour la chaîne d'entrée 00. Puisque l'un des chemins mène à un état final, 00 est accepté par le NFA ci-dessus.
Quelques points importants :
- Justification:
In case of DFA ? : Q X ? -->Q En cas de NFA ? :QX ? --> 2Q>
Maintenant, si vous observez, vous découvrirez Q X ? -> Q fait partie de Q X ? -> 2Q.
Du côté RHS, Q est le sous-ensemble de 2Qce qui indique que Q est contenu dans 2Qou Q fait partie de 2Q, cependant, l’inverse n’est pas vrai. Donc mathématiquement, on peut conclure que chaque DFA est NFA mais pas l'inverse . Pourtant, il existe un moyen de convertir un NFA en DFA, donc il existe un DFA équivalent pour chaque NFA .
- NFA et DFA ont le même pouvoir et chaque NFA peut être traduit en DFA.
- Il peut y avoir plusieurs états finaux dans DFA et NFA.
- NFA est davantage un concept théorique.
- DFA est utilisé dans l'analyse lexicale du compilateur.
- Si le nombre d'états dans le NFA est N alors, son DFA peut avoir au maximum 2Nnombre d'états.
Voir Quiz sur les expressions régulières et les automates finis .
