Les triangles sont des polygones fermés à trois côtés formés par l'intersection de trois lignes. On le rencontre beaucoup dans la vie de tous les jours. C'est l'une des formes de base de la géométrie. Il a trois côtés, trois angles et trois sommets. Un triangle rectangle est un triangle dont l'un des angles est toujours égal à 90°. Théorème de Pythagore est dérivé pour les triangles rectangles, qui stipule que le carré de l'hypoténuse (le côté le plus long) est égal à la somme des carrés de base et perpendiculaire.
Étant donné la longueur d’au moins deux côtés d’un triangle rectangle, nous pouvons trouver la valeur de n’importe quel angle du triangle rectangle. Pour cela, nous utilisons diverses fonctions trigonométriques comme le sinus, le cosinus, la tangente, la cotangente, la sec et le cosec. Ceux-ci nous aident à relier les angles d’un triangle rectangle avec ses côtés.
Propriétés
- Il existe un sommet à angle droit parmi les trois sommets
- Le côté opposé au sommet de l’angle droit est appelé le hypoténuse .
- La longueur des côtés suit le théorème de Pythagore, qui énonce
hypoténuse 2 = socle 2 + dénivelé 2
- L'hypoténuse est le côté le plus long d'un triangle rectangle.
- Les angles autres que l'angle droit sont des angles aigus puisque la valeur est inférieure à 90Ô
Fonctions trigonométriques
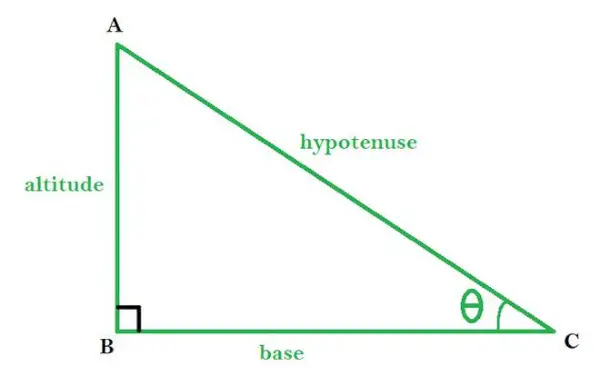
ABC est un triangle rectangle avec ∠B comme angle droit
méthodes en java
- cosθ : Cela donne le rapport de la base par l’hypoténuse d’un triangle rectangle.
cosθ = base / hypoténuse
- péchéθ : Cela donne le rapport de l'altitude par l'hypoténuse d'un triangle rectangle.
sinθ = altitude / hypoténuse
- tanθ : C'est le rapport de l'altitude par la base d'un triangle rectangle.
tanθ = altitude / base
- lit bébéθ : C'est l'inverse de tanθ
- secθ : C'est l'inverse de cosθ
- cosecθ : C'est l'inverse de sinθ
Pour trouver les angles d’un triangle rectangle, on peut prendre l’inverse trigonométrique du rapport des côtés donnés du triangle.
Exemple:
Si sinθ = x, alors on peut écrire
θ = péché -1 X.
Cela renvoie l'angle pour lequel la valeur sinusoïdale de l'angle est x.
De même, il existe parce que-1θ, donc-1moi, lit bébé-1θ, seconde-1θ et cosec-1je
Exemples de problèmes
Question 1. Étant donné un triangle rectangle, dont la base est égale à 10 cm et l'hypoténuse est égale à 20 cm. Trouvez la valeur de l'angle de base.
Solution:
Étant donné, base = 10 cm
Hypoténuse = 20 cm
Soit la valeur de l'angle de base θ. Nous pouvons écrire
cosθ = base / hypoténuse = 10/20 = 1/2
θ = cos-1(1/2) = 60Ô
Ainsi, la valeur de l'angle de base est de 60 Ô .
Question 2. Trouvez la valeur des angles d'un triangle droit, étant donné que l'un des angles aigus est le double de l'autre.
Solution:
Puisque nous savons que la somme des trois angles d’un triangle est 180Ô.
Puisque l'un des angles est de 90Ôet l’un des angles aigus est le double de l’autre, on peut les considérer comme θ et 2θ.
On peut donc écrire
90Ô+ θ + 2θ = 180Ô
3θ = 180Ô– 90Ô
3θ = 90Ô
θ = 90Ô/3 = 30 Ô
2θ = 2 × 30Ô= 60 Ô
Donc les angles sont 30 Ô , 60 Ô , et 90 Ô .
Question 3. Trouvez la valeur de l'angle d'élévation d'une échelle de longueur 5 m, étant donné que la base de l'échelle est à une distance de 3 m du mur.
Solution:
Puisque l’échelle agit comme l’hypoténuse d’un triangle rectangle et que la distance de base est égale à 3 m, on peut écrire
Hypoténuse = 5m
Socle = 3m
Soit l'angle d'élévation θ. On peut donc écrire
cosθ = Base / Hypoténuse = 3/5
θ = cos-1(3/5)
θ = 53Ô
Ainsi, la valeur de l'angle d'élévation est de 53Ô.
Question 4. Trouvez la valeur de l'hypoténuse, étant donné que la longueur de l'altitude est de 8 m et que l'angle de base est égal à 30. Ô .
Solution:
Étant donné, l'angle de base est égal à 30Ôet l'altitude est égale à 8 m, nous pouvons appliquer la fonction sinus pour trouver la longueur de l'hypoténuse.
sin30 Ô = altitude / hypoténuse
hypoténuse = altitude / sin30Ô
Puisque la valeur de sin30Ôest égal à 1/2, on peut écrire
hypoténuse = altitude / (1/2) = 2 × altitude
Ainsi, hypoténuse = 2 × 8 = 16m
Ainsi, la longueur de l'hypoténuse est égale à 16 m.
