L'algorithme de Ford-Fulkerson est un algorithme largement utilisé pour résoudre le problème de débit maximal dans un réseau à flux. Le problème du flux maximal consiste à déterminer la quantité maximale de flux pouvant être envoyée d’un sommet source à un sommet récepteur dans un graphe pondéré orienté, sous réserve de contraintes de capacité sur les arêtes.
L'algorithme fonctionne en trouvant de manière itérative un chemin d'augmentation, qui est un chemin allant de la source au puits dans le graphe résiduel, c'est-à-dire le graphe obtenu en soustrayant le flux de courant de la capacité de chaque bord. L’algorithme augmente ensuite le flux le long de ce chemin du montant maximum possible, qui correspond à la capacité minimale des bords le long du chemin.
Problème:
Étant donné un graphique qui représente un réseau de flux où chaque arête a une capacité. De plus, étant donné deux sommets source 'sable couler 't' dans le graphique, trouvez le flux maximum possible de s à t avec les contraintes suivantes :
- Le débit sur un bord ne dépasse pas la capacité donnée du bord.
- Le flux entrant est égal au flux sortant pour chaque sommet sauf s et t.
Par exemple, considérons le graphique suivant tiré du livre CLRS.
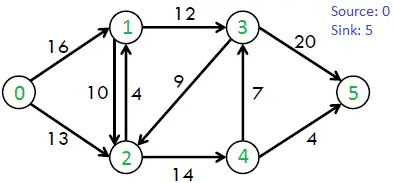
Le débit maximum possible dans le graphique ci-dessus est de 23.

Prérequis : Introduction au problème de débit maximum
Algorithme de Ford-Fulkerson
Voici une idée simple de l'algorithme de Ford-Fulkerson :
- Commencez avec un débit initial égal à 0.
- Bien qu'il existe un chemin croissant de la source au récepteur :
- Trouvez un chemin croissant à l'aide de n'importe quel algorithme de recherche de chemin, tel que la recherche en largeur ou la recherche en profondeur.
- Déterminez la quantité de flux qui peut être envoyée le long du chemin d’augmentation, qui correspond à la capacité résiduelle minimale le long des bords du chemin.
- Augmentez le débit le long du chemin d'augmentation de la quantité déterminée.
- Renvoie le débit maximum.
Complexité temporelle : La complexité temporelle de l'algorithme ci-dessus est O(max_flow * E). Nous exécutons une boucle tant qu'il existe un chemin croissant. Dans le pire des cas, nous pouvons ajouter 1 flux unitaire à chaque itération. Par conséquent, la complexité temporelle devient O(max_flow * E).
obtenir une connexion
Comment implémenter l’algorithme simple ci-dessus ?
Définissons d'abord le concept de graphe résiduel qui est nécessaire à la compréhension de l'implémentation.
Graphique résiduel d'un réseau de flux est un graphique qui indique un flux supplémentaire possible. S'il existe un chemin depuis la source jusqu'au puits dans le graphique résiduel, il est alors possible d'ajouter un flux. Chaque arête d'un graphe résiduel a une valeur appelée capacité résiduelle qui est égale à la capacité originale du bord moins le flux de courant. La capacité résiduelle est essentiellement la capacité actuelle du périphérique.
Parlons maintenant des détails de mise en œuvre. La capacité résiduelle est égale à 0 s'il n'y a pas d'arête entre deux sommets du graphe résiduel. Nous pouvons initialiser le graphe résiduel comme graphe d'origine car il n'y a pas de flux initial et la capacité résiduelle initiale est égale à la capacité d'origine. Pour trouver un chemin croissant, nous pouvons soit faire un BFS ou un DFS du graphe résiduel. Nous avons utilisé BFS dans l'implémentation ci-dessous. En utilisant BFS, nous pouvons découvrir s'il existe un chemin de la source au récepteur. BFS construit également le tableau parent[]. À l'aide du tableau parent[], nous parcourons le chemin trouvé et trouvons un flux possible via ce chemin en trouvant la capacité résiduelle minimale le long du chemin. Nous ajoutons ensuite le flux de chemin trouvé au flux global.
longueur de la chaîne Java
L'important est que nous devons mettre à jour les capacités résiduelles dans le graphique résiduel. Nous soustrayons le flux de chemin de tous les bords le long du chemin et nous ajoutons le flux de chemin le long des bords inverses. Nous devons ajouter le flux de chemin le long des bords inverses car il faudra peut-être plus tard envoyer le flux dans la direction inverse (voir le lien suivant par exemple).
Vous trouverez ci-dessous l'implémentation de l'algorithme de Ford-Fulkerson. Pour simplifier les choses, le graphique est représenté comme une matrice 2D.
C++
// C++ program for implementation of Ford Fulkerson> // algorithm> #include> #include> #include> #include> using> namespace> std;> // Number of vertices in given graph> #define V 6> /* Returns true if there is a path from source 's' to sink> >'t' in residual graph. Also fills parent[] to store the> >path */> bool> bfs(>int> rGraph[V][V],>int> s,>int> t,>int> parent[])> {> >// Create a visited array and mark all vertices as not> >// visited> >bool> visited[V];> >memset>(visited, 0,>sizeof>(visited));> >// Create a queue, enqueue source vertex and mark source> >// vertex as visited> >queue<>int>>q;> >q.push(s);> >visited[s] =>true>;> >parent[s] = -1;> >// Standard BFS Loop> >while> (!q.empty()) {> >int> u = q.front();> >q.pop();> >for> (>int> v = 0; v if (visited[v] == false && rGraph[u][v]>0) { // Si nous trouvons une connexion au nœud récepteur, // alors cela ne sert à rien dans BFS. Nous // devons juste définir son parent et pouvons retourner // true if (v == t) { parent[ v] = vous; renvoie vrai ; } q.push(v); parent[v] = vous; visité[v] = vrai; } } } // Nous n'avons pas atteint le récepteur dans BFS à partir de la source, donc // return false return false; } // Renvoie le flux maximum de s à t dans le graphique donné int fordFulkerson(int graph[V][V], int s, int t) { int u, v; // Crée un graphe résiduel et remplit le graphe résiduel // avec les capacités données dans le graphe d'origine comme // capacités résiduelles dans le graphe résiduel int rGraph[V] [V]; // Graphique résiduel où rGraph[i][j] // indique la capacité résiduelle du bord // de i à j (s'il y a un bord. Si // rGraph[i][j] vaut 0, alors il n'y en a pas) for (u = 0; u for (v = 0; v rGraph[u][v] = graph[u][v]; int parent[V]; // Ce tableau est rempli par BFS et // stocke le chemin int max_flow = 0; // Il n'y a pas de flux initialement // Augmente le flux tant qu'il y a un chemin de la source vers // le puits while (bfs(rGraph, s, t, parent)) { // Trouver la capacité résiduelle minimale des bords le long // du chemin rempli par BFS. Ou nous pouvons dire trouver le // flux maximum à travers le chemin trouvé. int path_flow = INT_MAX; for (v = t; v != s; v = parent[v]) { u = parent[v]; path_flow = min(path_flow, rGraph[u][v]); } // met à jour les capacités résiduelles des arêtes et // inverse les arêtes le long du chemin pour (v = t; v != s; v = parent[v]) { u = parent[v]; rGraph[u][v] -= path_flow; rGraph[v][u] += path_flow; } // Ajouter le flux de chemin au flux global max_flow += path_flow; // Renvoie le flux global return max_flow; } // Programme pilote pour tester les fonctions ci-dessus int main() { // Créons un graphique montré dans l'exemple ci-dessus int graph[V][V] = { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 }, { 0, 4, 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 }, { 0, 0, 0, 7 , 0, 4 }, { 0, 0, 0, 0, 0, 0 } } ; cout<< 'The maximum possible flow is ' << fordFulkerson(graph, 0, 5); return 0; }> |
>
>
Java
// Java program for implementation of Ford Fulkerson> // algorithm> import> java.io.*;> import> java.lang.*;> import> java.util.*;> import> java.util.LinkedList;> class> MaxFlow {> >static> final> int> V =>6>;>// Number of vertices in graph> >/* Returns true if there is a path from source 's' to> >sink 't' in residual graph. Also fills parent[] to> >store the path */> >boolean> bfs(>int> rGraph[][],>int> s,>int> t,>int> parent[])> >{> >// Create a visited array and mark all vertices as> >// not visited> >boolean> visited[] =>new> boolean>[V];> >for> (>int> i =>0>; i visited[i] = false; // Create a queue, enqueue source vertex and mark // source vertex as visited LinkedList queue = new LinkedList(); queue.add(s); visited[s] = true; parent[s] = -1; // Standard BFS Loop while (queue.size() != 0) { int u = queue.poll(); for (int v = 0; v if (visited[v] == false && rGraph[u][v]>0) { // Si nous trouvons une connexion au nœud // récepteur, alors cela ne sert à rien dans BFS // Nous devons juste définir son parent // et pouvons renvoyer true if (v == t) { parent[ v] = vous; renvoie vrai ; } queue.add(v); parent[v] = vous; visité[v] = vrai; } } } // Nous n'avons pas atteint le récepteur dans BFS à partir de la source, // donc return false return false; } // Renvoie le flux maximum de s à t dans le // graphique donné int fordFulkerson(int graph[][], int s, int t) { int u, v; // Crée un graphe résiduel et remplit le graphe résiduel // avec les capacités données dans le graphe d'origine // en tant que capacités résiduelles dans le graphe résiduel // Graphe résiduel où rGraph[i][j] indique // la capacité résiduelle du bord de i à j (s'il // y a une arête. Si rGraph[i][j] vaut 0, alors il n'y en a // pas) int rGraph[][] = new int[V][V]; for (u = 0; u for (v = 0; v rGraph[u][v] = graph[u][v]; // Ce tableau est rempli par BFS et pour stocker le chemin int parent[] = new int[ V]; int max_flow = 0; // Il n'y a pas de flux initialement // Augmente le flux tant qu'il y a un chemin depuis la source // vers le puits while (bfs(rGraph, s, t, parent)) { // Trouver la capacité résiduelle minimale des bords // le long du chemin rempli par BFS. Ou nous pouvons dire // trouver le flux maximum à travers le chemin trouvé. int path_flow = Integer.MAX_VALUE; for (v = t; v != s; v = parent[v ]) { u = parent[v]; path_flow = Math.min(path_flow, rGraph[u][v]); // met à jour les capacités résiduelles des arêtes et // inverse les arêtes le long du chemin pour (v = t; v != s; v = parent[v]) { u = parent[v]; rGraph[u][v] -= path_flow; rGraph[v][u] += path_flow; flow max_flow += path_flow; } // Renvoie le flux global return max_flow; } // Programme pilote pour tester les fonctions ci-dessus public static void main(String[] args) throws java.lang.Exception { // Créons un graphique affiché dans l'exemple ci-dessus int graph[][] = new int[][] { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 }, { 0, 4 , 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 }, { 0, 0, 0, 7, 0, 4 }, { 0, 0, 0, 0, 0, 0 } } ; MaxFlow m = nouveau MaxFlow(); System.out.println('Le débit maximum possible est ' + m.fordFulkerson(graph, 0, 5)); } }> |
>
opérateur Java
>
Python
# Python program for implementation> # of Ford Fulkerson algorithm> from> collections>import> defaultdict> # This class represents a directed graph> # using adjacency matrix representation> class> Graph:> >def> __init__(>self>, graph):> >self>.graph>=> graph># residual graph> >self>. ROW>=> len>(graph)> ># self.COL = len(gr[0])> >'''Returns true if there is a path from source 's' to sink 't' in> >residual graph. Also fills parent[] to store the path '''> >def> BFS(>self>, s, t, parent):> ># Mark all the vertices as not visited> >visited>=> [>False>]>*>(>self>.ROW)> ># Create a queue for BFS> >queue>=> []> ># Mark the source node as visited and enqueue it> >queue.append(s)> >visited[s]>=> True> ># Standard BFS Loop> >while> queue:> ># Dequeue a vertex from queue and print it> >u>=> queue.pop(>0>)> ># Get all adjacent vertices of the dequeued vertex u> ># If a adjacent has not been visited, then mark it> ># visited and enqueue it> >for> ind, val>in> enumerate>(>self>.graph[u]):> >if> visited[ind]>=>=> False> and> val>>0>:> ># If we find a connection to the sink node,> ># then there is no point in BFS anymore> ># We just have to set its parent and can return true> >queue.append(ind)> >visited[ind]>=> True> >parent[ind]>=> u> >if> ind>=>=> t:> >return> True> ># We didn't reach sink in BFS starting> ># from source, so return false> >return> False> > > ># Returns the maximum flow from s to t in the given graph> >def> FordFulkerson(>self>, source, sink):> ># This array is filled by BFS and to store path> >parent>=> [>->1>]>*>(>self>.ROW)> >max_flow>=> 0> # There is no flow initially> ># Augment the flow while there is path from source to sink> >while> self>.BFS(source, sink, parent) :> ># Find minimum residual capacity of the edges along the> ># path filled by BFS. Or we can say find the maximum flow> ># through the path found.> >path_flow>=> float>(>'Inf'>)> >s>=> sink> >while>(s !>=> source):> >path_flow>=> min> (path_flow,>self>.graph[parent[s]][s])> >s>=> parent[s]> ># Add path flow to overall flow> >max_flow>+>=> path_flow> ># update residual capacities of the edges and reverse edges> ># along the path> >v>=> sink> >while>(v !>=> source):> >u>=> parent[v]> >self>.graph[u][v]>->=> path_flow> >self>.graph[v][u]>+>=> path_flow> >v>=> parent[v]> >return> max_flow> > # Create a graph given in the above diagram> graph>=> [[>0>,>16>,>13>,>0>,>0>,>0>],> >[>0>,>0>,>10>,>12>,>0>,>0>],> >[>0>,>4>,>0>,>0>,>14>,>0>],> >[>0>,>0>,>9>,>0>,>0>,>20>],> >[>0>,>0>,>0>,>7>,>0>,>4>],> >[>0>,>0>,>0>,>0>,>0>,>0>]]> g>=> Graph(graph)> source>=> 0>; sink>=> 5> > print> (>'The maximum possible flow is %d '> %> g.FordFulkerson(source, sink))> # This code is contributed by Neelam Yadav> |
>
>
C#
// C# program for implementation> // of Ford Fulkerson algorithm> using> System;> using> System.Collections.Generic;> public> class> MaxFlow {> >static> readonly> int> V = 6;>// Number of vertices in> >// graph> >/* Returns true if there is a path> >from source 's' to sink 't' in residual> >graph. Also fills parent[] to store the> >path */> >bool> bfs(>int>[, ] rGraph,>int> s,>int> t,>int>[] parent)> >{> >// Create a visited array and mark> >// all vertices as not visited> >bool>[] visited =>new> bool>[V];> >for> (>int> i = 0; i visited[i] = false; // Create a queue, enqueue source vertex and mark // source vertex as visited List |
>
instruction if else en java
>
Javascript
> // Javascript program for implementation of Ford> // Fulkerson algorithm> // Number of vertices in graph> let V = 6;> // Returns true if there is a path from source> // 's' to sink 't' in residual graph. Also> // fills parent[] to store the path> function> bfs(rGraph, s, t, parent)> {> > >// Create a visited array and mark all> >// vertices as not visited> >let visited =>new> Array(V);> >for>(let i = 0; i visited[i] = false; // Create a queue, enqueue source vertex // and mark source vertex as visited let queue = []; queue.push(s); visited[s] = true; parent[s] = -1; // Standard BFS Loop while (queue.length != 0) { let u = queue.shift(); for(let v = 0; v { if (visited[v] == false && rGraph[u][v]>0) { // Si nous trouvons une connexion au nœud // récepteur, alors cela ne sert à rien dans BFS // Nous devons juste définir son parent // et pouvons renvoyer true if (v == t) { parent[ v] = vous; renvoie vrai ; } queue.push(v); parent[v] = vous; visité[v] = vrai; } } } // Nous n'avons pas atteint le récepteur dans BFS à partir // de la source, donc return false return false; } // Renvoie le flux maximum de s à t dans // la fonction graphique donnée fordFulkerson(graph, s, t) { let u, v; // Créez un graphique résiduel et remplissez le // graphique résiduel avec des capacités données // dans le graphique d'origine en tant que résidu // capacités dans le graphique résiduel // Graphique résiduel où rGraph[i][j] // indique la capacité résiduelle du bord / / de i à j (s'il y a une arête. // Si rGraph[i][j] vaut 0, alors il n'y en a // pas) let rGraph = new Array(V); for(u = 0; u { rGraph[u] = new Array(V); for(v = 0; v rGraph[u][v] = graph[u][v]; } // Ce tableau est rempli par BFS et pour stocker le chemin let parent = new Array(V); // Il n'y a pas de flux initialement let max_flow = 0; // Augmente le flux tant qu'il existe // un chemin de la source au récepteur while (bfs(rGraph, s, t , parent)) { // Trouver la capacité résiduelle minimale des bords // le long du chemin rempli par BFS. Ou nous pouvons dire // trouver le flux maximum à travers le chemin trouvé. ; v != s; v = parent[v]) { u = parent[v]; Math.min(path_flow, rGraph[u][v]); inverser les arêtes le long du chemin for(v = t; v != s; v = parent[v]) { u = parent[v]; rGraph[u][v] -= path_flow; = path_flow; } // Ajouter le flux de chemin au flux global max_flow += path_flow; } // Renvoie le flux global return max_flow; } // Code du pilote // Créons un graphique montré dans l'exemple ci-dessus let graph = [ [ 0 , 16, 13, 0, 0, 0 ], [ 0, 0, 10, 12, 0, 0 ], [ 0, 4, 0, 0, 14, 0 ], [ 0, 0, 9, 0, 0 , 20 ], [ 0, 0, 0, 7, 0, 4 ], [ 0, 0, 0, 0, 0, 0 ] ] ; document.write('Le débit maximum possible est ' + fordFulkerson(graph, 0, 5)); // Ce code est contribué par avanitrachhadiya2155> |
>
lion comparé à un tigre
>Sortir
The maximum possible flow is 23>
Complexité temporelle : O(|V| * E^2) , où E est le nombre d'arêtes et V est le nombre de sommets.
Complexité spatiale :O(V) , pendant que nous créions la file d'attente.
L'implémentation ci-dessus de l'algorithme Ford Fulkerson est appelée Algorithme d'Edmonds-Karp . L'idée d'Edmonds-Karp est d'utiliser BFS dans l'implémentation de Ford Fulkerson, car BFS choisit toujours un chemin avec un nombre minimum d'arêtes. Lorsque BFS est utilisé, la complexité temporelle du pire cas peut être réduite à O(VE2). L'implémentation ci-dessus utilise une représentation matricielle de contiguïté, mais où BFS prend O(V2), la complexité temporelle de l'implémentation ci-dessus est O(EV3) (Référer Livre CLRS pour preuve de complexité temporelle)
Il s’agit d’un problème important car il se pose dans de nombreuses situations pratiques. Les exemples incluent la maximisation du transport avec des limites de trafic données, la maximisation du flux de paquets dans les réseaux informatiques.
Algorithme de Dinc pour Max-Flow.
Exercice:
Modifiez l'implémentation ci-dessus pour qu'elle s'exécute en O(VE2) temps.
