La suppression d'un nœud d'une arborescence AVL est similaire à celle d'une arborescence de recherche binaire. La suppression peut perturber le facteur d'équilibre d'un arbre AVL et, par conséquent, l'arbre doit être rééquilibré afin de maintenir l'AVL. Pour cela, nous devons effectuer des rotations. Les deux types de rotations sont la rotation L et la rotation R. Ici, nous discuterons des rotations R. Les rotations L en sont les images miroir.
Si le nœud à supprimer est présent dans le sous-arbre gauche du nœud critique, alors la rotation L doit être appliquée sinon si le nœud à supprimer est présent dans le sous-arbre droit du nœud critique. , la rotation R sera appliquée.
Considérons que A est le nœud critique et B est le nœud racine de son sous-arbre gauche. Si le nœud X, présent dans le sous-arbre droit de A, doit être supprimé, alors il peut y avoir trois situations différentes :
Rotation R0 (le nœud B a un facteur d'équilibre de 0)
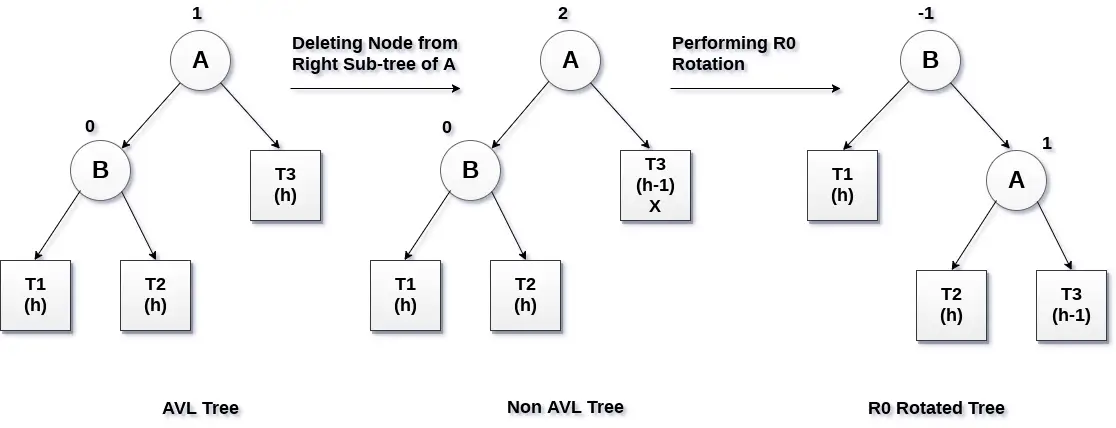
Si le nœud B a un facteur d'équilibre de 0 et que le facteur d'équilibre du nœud A est perturbé lors de la suppression du nœud X, alors l'arbre sera rééquilibré en faisant tourner l'arbre en utilisant la rotation R0.
Le nœud critique A est déplacé vers sa droite et le nœud B devient la racine de l'arbre avec T1 comme sous-arbre gauche. Les sous-arbres T2 et T3 deviennent les sous-arbres gauche et droit du nœud A. le processus impliqué dans la rotation R0 est illustré dans l'image suivante.
Exemple:
Supprimez le nœud 30 de l'arborescence AVL affichée dans l'image suivante.

Solution
Dans ce cas, le nœud B a un facteur d'équilibre de 0, donc l'arbre subira une rotation en utilisant la rotation R0 comme indiqué dans l'image suivante. Le nœud B(10) devient la racine, tandis que le nœud A est déplacé vers sa droite. L'enfant droit du nœud B deviendra désormais l'enfant gauche du nœud A.
modèles de logiciels Java

Rotation R1 (le nœud B a un facteur d'équilibre de 1)
La rotation R1 doit être effectuée si le facteur d'équilibre du nœud B est de 1. Dans la rotation R1, le nœud critique A est déplacé vers sa droite avec les sous-arbres T2 et T3 comme enfants respectivement gauche et droit. T1 doit être placé comme sous-arbre gauche du nœud B.
Le processus impliqué dans la rotation R1 est illustré dans l'image suivante.

Exemple
Supprimez le nœud 55 de l’arborescence AVL affichée dans l’image suivante.

Solution :
La suppression de 55 de l'arbre AVL perturbe le facteur d'équilibre du nœud 50, c'est-à-dire le nœud A qui devient le nœud critique. C'est la condition de rotation R1 dans laquelle le nœud A sera déplacé vers sa droite (illustré dans l'image ci-dessous). La droite de B est maintenant devenue la gauche de A (soit 45).
Le processus impliqué dans la solution est illustré dans l’image suivante.

Rotation R-1 (le nœud B a un facteur d'équilibre -1)
La rotation R-1 doit être effectuée si le nœud B a un facteur d'équilibre -1. Ce cas est traité de la même manière que la rotation LR. Dans ce cas, le nœud C, qui est l’enfant droit du nœud B, devient le nœud racine de l’arbre avec B et A comme enfants respectivement gauche et droit.
Les sous-arbres T1, T2 deviennent les sous-arbres gauche et droit de B tandis que T3, T4 deviennent les sous-arbres gauche et droit de A.
pour un tableau de chaînes Java
Le processus impliqué dans la rotation R-1 est illustré dans l'image suivante.

Exemple
Supprimez le nœud 60 de l'arborescence AVL affichée dans l'image suivante.

Solution:
dans ce cas, le nœud B a un facteur d'équilibre -1. La suppression du nœud 60 perturbe le facteur d'équilibre du nœud 50, il doit donc subir une rotation R-1. Le nœud C, c'est-à-dire 45, devient la racine de l'arbre avec les nœuds B(40) et A(50) comme enfants gauche et droit.

