Nous connaissons un arbre est une structure de données non linéaire. Il n'y a aucune limitation quant au nombre d'enfants. UNQu’est-ce qu’un arbre binaire complet ?
Un arbre binaire complet est un type spécial d'arbre binaire dans lequel tous les niveaux de l'arbre sont remplis complètement, à l'exception des nœuds de niveau le plus bas qui sont remplis du plus à gauche possible.

Arbre binaire complet
Quelques termes relatifs à l'arbre binaire complet :
- Racine – Nœud dans lequel aucun arc ne provient du parent. Exemple - nœud A
- Enfant – Le nœud ayant un bord entrant est appelé enfant. Exemple – les nœuds B, F sont respectivement les enfants de A et C.
- Frère et sœur – Les nœuds ayant le même parent sont frères. Exemple : D, E sont frères et sœurs car ils ont le même parent B.
- Degré d'un nœud – Nombre d'enfants d'un parent particulier. Exemple - Le degré de A est 2 et le degré de C est 1. Le degré de D est 0.
- Nœuds internes/externes – Les nœuds feuilles sont des nœuds externes et les nœuds non feuilles sont des nœuds internes.
- Niveau – Compter les nœuds dans un chemin pour atteindre un nœud de destination. Exemple - Le niveau du nœud D est 2 car les nœuds A et B forment le chemin.
- Hauteur – Nombre d'arêtes pour atteindre le nœud de destination, la racine est à la hauteur 0. Exemple – La hauteur du nœud E est de 2 car il a deux arêtes à partir de la racine.
Propriétés de l'arbre binaire complet :
- Un arbre binaire complet est dit un arbre binaire proprement dit où toutes les feuilles ont la même profondeur.
- Dans un arbre binaire complet, nombre de nœuds en profondeur d est 2 d .
- Dans un arbre binaire complet avec n la hauteur des nœuds de l’arbre est journal(n+1) .
- Tous les niveaux sauf le dernier niveau sont complètement remplis.
Arbre binaire parfait vs arbre binaire complet :
Un arbre binaire de hauteur « h » ayant le nombre maximum de nœuds est un parfait arbre binaire.
Pour une hauteur donnée h , le nombre maximum de nœuds est 2 h+1 -1 .
UN complet l'arbre binaire de hauteur h est un arbre binaire parfait jusqu'à la hauteur h-1 , et dans le dernier niveau, les éléments sont stockés dans l'ordre de gauche à droite.
Exemple 1:
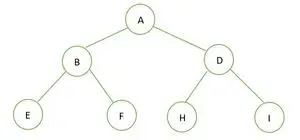
Un arbre binaire
La hauteur de l'arbre binaire donné est 2 et le nombre maximum de nœuds dans cet arbre est n= 2h+1-1 = 22+1-1 = 23-1 = 7 .
On peut donc conclure que c'est un arbre binaire parfait .
Passons maintenant à un arbre binaire complet, il est plein jusqu'en hauteur h-1 c'est à dire.; 1, et les éléments du dernier niveau sont stockés dans l'ordre de gauche à droite. Il s’agit donc également d’un arbre binaire complet. Voici la représentation des éléments lorsqu'ils sont stockés dans un tableau

Élément stocké dans un tableau niveau par niveau
Dans le tableau, tous les éléments sont stockés en continu.
Exemple 2 :
chaîne de fractionnement c++
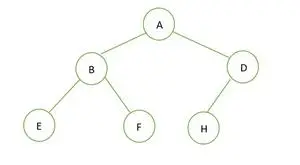
Un arbre binaire
La hauteur de l'arbre binaire donné est de 2 et le nombre maximum de nœuds qui devraient s'y trouver est de 2h+1– 1 = 22+1– 1 = 23– 1 = 7 .
Mais le nombre de nœuds dans l’arbre est 6 . C'est donc pas un arbre binaire parfait .
Passons maintenant à un arbre binaire complet, il est plein jusqu'en hauteur h-1 c'est à dire.; 1 , et l'élément du dernier niveau sont stockés dans l'ordre de gauche à droite. Il s'agit donc d'un arbre binaire complet . Stockez l'élément dans un tableau et ce sera comme :
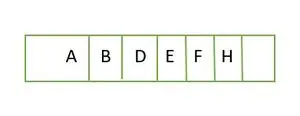
Élément stocké dans un tableau niveau par niveau
Exemple 3 :
polymorphisme
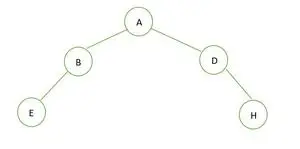
Un arbre binaire
La hauteur de l'arbre binaire est de 2 et le nombre maximum de nœuds pouvant s'y trouver est de 7, mais il n'y a que 5 nœuds donc c'est pas un arbre binaire parfait .
Dans le cas d'un arbre binaire complet, on voit qu'au dernier niveau les éléments ne sont pas remplis de gauche à droite. Donc c'est pas un arbre binaire complet .
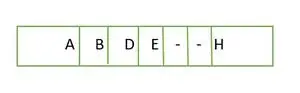
Élément stocké dans un tableau niveau par niveau
Les éléments du tableau ne sont pas continus.
Arbre binaire complet vs arbre binaire complet :
Pour un arbre binaire complet, chaque nœud a soit 2 enfants, soit 0 enfant.
Exemple 1:
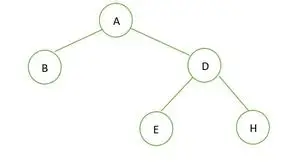
Un arbre binaire
Dans l'arbre binaire donné, il n'y a pas de nœud ayant le degré 1, soit 2 ou 0 enfants pour chaque nœud, donc c'est un arbre binaire complet .
Pour un arbre binaire complet, les éléments sont stockés niveau par niveau et non du côté le plus à gauche du dernier niveau. C'est donc pas un arbre binaire complet . La représentation du tableau est :
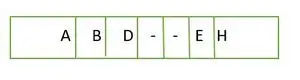
Élément stocké dans un tableau niveau par niveau
Exemple 2 :
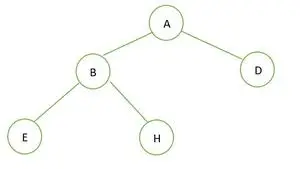
Un arbre binaire
Dans l'arbre binaire donné, il n'y a aucun nœud de degré 1. Chaque nœud a un degré de 2 ou de 0. C'est donc un arbre binaire complet .
Pour un arbre binaire complet, les éléments sont stockés niveau par niveau et remplis à partir du côté le plus à gauche du dernier niveau. D'où cela un arbre binaire complet . Vous trouverez ci-dessous la représentation matricielle de l'arbre :
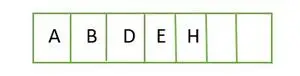
Élément stocké dans un tableau niveau par niveau
Exemple 3 :
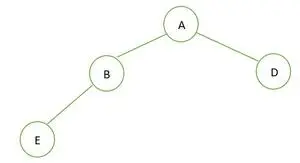
Un arbre binaire
Dans l'arbre binaire donné, le nœud B a le degré 1, ce qui viole la propriété de l'arbre binaire complet, il est donc pas un arbre binaire complet
liste de liens Java
Pour un arbre binaire complet, les éléments sont stockés niveau par niveau et remplis à partir du côté le plus à gauche du dernier niveau. Il s'agit donc d'un arbre binaire complet . La représentation matricielle de l'arbre binaire est :
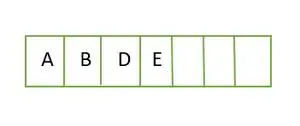
Élément stocké dans un tableau niveau par niveau
Exemple 4 :
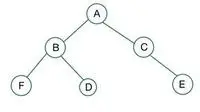
un arbre binaire
Sridevi
Dans l'arbre binaire donné, le nœud C a le degré 1, ce qui viole la propriété d'un arbre binaire complet, il est donc pas un arbre binaire complet
Pour un arbre binaire complet, les éléments sont stockés niveau par niveau et remplis à partir du côté le plus à gauche du dernier niveau. Ici, le nœud E viole la condition. C'est donc pas un arbre binaire complet .
Création d'un arbre binaire complet :
Nous connaissons un arbre binaire complet est un arbre dans lequel, à l'exception du dernier niveau (disons je )tous les autres niveaux ont ( 2l ) les nœuds et les nœuds sont alignés de gauche à droite.
Il peut être représenté à l'aide d'un tableau. Si le parent est-il index je donc l'enfant de gauche est à 2i+1 et le bon enfant est à 2i+2 .
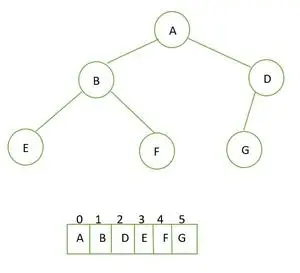
Arbre binaire complet et sa représentation matricielle
Algorithme:
Pour la création d'un Arbre binaire complet , nous avons besoin d'un Étape 1: Initialisez la racine avec un nouveau nœud lorsque l'arborescence est vide.
Étape 2: Si l'arborescence n'est pas vide, récupérez l'élément frontal
- Si l'élément avant n'a pas d'enfant gauche, définissez l'enfant gauche sur un nouveau nœud
- Si le bon enfant n'est pas présent, définissez le bon enfant comme nouveau nœud
Étape 3: Si le nœud a les deux enfants alors populaire il de la file d'attente.
Étape 4: Mettez les nouvelles données en file d’attente.
Illustration:
Considérez le tableau ci-dessous :
tri par sélection Java1. Le 1er élément sera la racine (valeur à l'index = 0 )
A est pris comme racine
2. L'élément suivant (à index = 1 ) sera la gauche et le troisième élément (index = 2 ) sera le bon enfant de root
B comme enfant de gauche et D comme enfant de droite
3. quatrième (indice = 3 ) et cinquième élément (index = 4 ) sera l'enfant gauche et droit du nœud B
E et F sont les enfants gauche et droit de B
4. Élément suivant (index = 5 ) restera enfant du nœud D
G est fait l'enfant gauche du nœud D
C'est ainsi qu'un arbre binaire complet est créé.
Mise en œuvre: Pour la mise en œuvre de la construction d'un arbre binaire complet à partir du parcours d'ordre de niveau est donné dans ce post .
Application de l'arbre binaire complet :
- Tri en tas
- Structure de données basée sur le tri par tas
Vérifiez si un arbre binaire donné est complet ou non : Suivre ce post pour vérifier si l'arbre binaire donné est complet ou non.




