Tri par seau est une technique de tri qui consiste à diviser les éléments en différents groupes, ou seaux. Ces godets sont formés en répartissant uniformément les éléments. Une fois les éléments divisés en compartiments, ils peuvent être triés à l’aide de n’importe quel autre algorithme de tri. Enfin, les éléments triés sont rassemblés de manière ordonnée.
Algorithme de tri de seau :
Créer n videz les compartiments (ou les listes) et procédez comme suit pour chaque élément du tableau arr[i].
- Insérer arr[i] dans le bucket[n*array[i]]
- Triez les compartiments individuels à l’aide du tri par insertion.
- Concaténez tous les buckets triés.
Comment fonctionne le tri par seau ?
Pour appliquer le tri par compartiment sur le tableau d'entrée [0,78, 0,17, 0,39, 0,26, 0,72, 0,94, 0,21, 0,12, 0,23, 0,68] , nous suivons ces étapes :
Étape 1: Créez un tableau de taille 10, où chaque emplacement représente un compartiment.
réseau et types de réseau

Création de buckets pour le tri
Étape 2: Insérez des éléments dans les compartiments à partir du tableau d'entrée en fonction de leur plage.
taille de police latex
Insertion d'éléments dans les buckets :
- Prenez chaque élément du tableau d’entrée.
- Multipliez l'élément par la taille du tableau de compartiments (10 dans ce cas). Par exemple, pour l'élément 0,23, nous obtenons 0,23 * 10 = 2,3.
- Convertissez le résultat en un entier, ce qui nous donne l'index du bucket. Dans ce cas, 2,3 est converti en entier 2.
- Insérez l'élément dans le bucket correspondant à l'index calculé.
- Répétez ces étapes pour tous les éléments du tableau d'entrée.
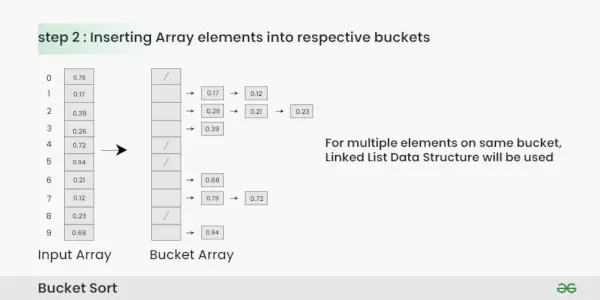
Insertion d'éléments de tableau dans les compartiments respectifs
Étape 3: Triez les éléments dans chaque compartiment. Dans cet exemple, nous utilisons le tri rapide (ou tout autre algorithme de tri stable) pour trier les éléments de chaque compartiment.
Trier les éléments dans chaque bucket :
- Appliquez un algorithme de tri stable (par exemple, tri à bulles, tri par fusion) pour trier les éléments dans chaque compartiment.
- Les éléments de chaque compartiment sont désormais triés.
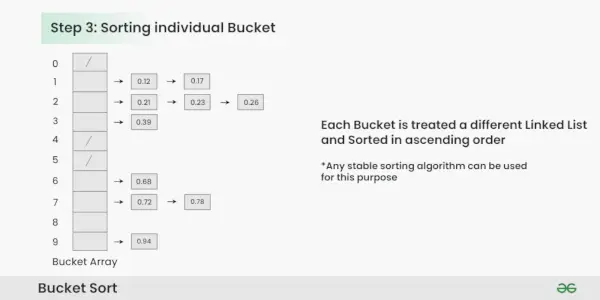
Tri des seaux individuels
Étape 4: Rassemblez les éléments de chaque compartiment et remettez-les dans le tableau d'origine.
Rassembler les éléments de chaque bucket :
- Parcourez chaque compartiment dans l’ordre.
- Insérez chaque élément individuel du compartiment dans le tableau d'origine.
- Une fois qu'un élément est copié, il est supprimé du bucket.
- Répétez ce processus pour tous les compartiments jusqu'à ce que tous les éléments aient été rassemblés.
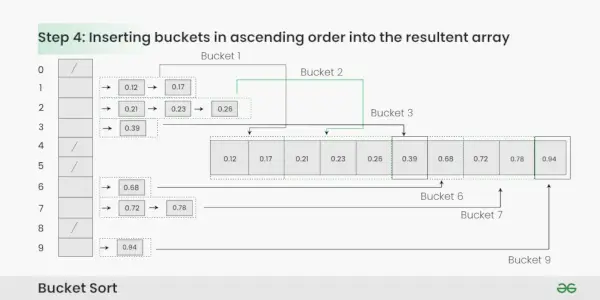
Insertion de buckets par ordre croissant dans le tableau résultant
mylivecricket.in
Étape 5 : Le tableau d'origine contient désormais les éléments triés.
Le tableau trié final utilisant le tri par compartiment pour l'entrée donnée est [0.12, 0.17, 0.21, 0.23, 0.26, 0.39, 0.68, 0.72, 0.78, 0.94].
Java bonjour programme

Renvoie le tableau trié
Implémentation de l'algorithme de tri par compartiment :
Vous trouverez ci-dessous l'implémentation du Bucket Sort :
C++ #include #include using namespace std; // Insertion sort function to sort individual buckets void insertionSort(vector& seau) { pour (int i = 1; i< bucket.size(); ++i) { float key = bucket[i]; int j = i - 1; while (j>= 0 && bucket[j]> clé) { bucket[j + 1] = bucket[j]; j--; } seau[j + 1] = clé ; } } // Fonction pour trier arr[] de taille n à l'aide du tri par bucket void bucketSort(float arr[], int n) { // 1) Créer un vecteur de n buckets videsb[n]; // 2) Placez les éléments du tableau dans différents compartiments pour (int i = 0; i< n; i++) { int bi = n * arr[i]; b[bi].push_back(arr[i]); } // 3) Sort individual buckets using insertion sort for (int i = 0; i < n; i++) { insertionSort(b[i]); } // 4) Concatenate all buckets into arr[] int index = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < b[i].size(); j++) { arr[index++] = b[i][j]; } } } // Driver program to test above function int main() { float arr[] = {0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434}; int n = sizeof(arr) / sizeof(arr[0]); bucketSort(arr, n); cout << 'Sorted array is
'; for (int i = 0; i < n; i++) { cout << arr[i] << ' '; } return 0; }>
Java import java.util.ArrayList; import java.util.List; public class Main { // Insertion sort function to sort individual buckets public static void insertionSort(Listseau) { pour (int je = 1; je< bucket.size(); ++i) { float key = bucket.get(i); int j = i - 1; while (j>= 0 && bucket.get(j)> clé) { bucket.set(j + 1, bucket.get(j)); j--; } bucket.set(j + 1, clé); } } // Fonction pour trier arr[] de taille n à l'aide du bucket sort public static void bucketSort(float[] arr) { int n = arr.length; // 1) Créer une liste de n buckets vides[] seaux = new ArrayList[n] ; pour (int je = 0; je< n; i++) { buckets[i] = new ArrayList(); } // 2) Put array elements in different buckets for (int i = 0; i < n; i++) { int bi = (int) (n * arr[i]); buckets[bi].add(arr[i]); } // 3) Sort individual buckets using insertion sort for (int i = 0; i < n; i++) { insertionSort(buckets[i]); } // 4) Concatenate all buckets into arr[] int index = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < buckets[i].size(); j++) { arr[index++] = buckets[i].get(j); } } } // Driver program to test above function public static void main(String[] args) { float[] arr = {0.897f, 0.565f, 0.656f, 0.1234f, 0.665f, 0.3434f}; bucketSort(arr); System.out.println('Sorted array is:'); for (float num : arr) { System.out.print(num + ' '); } } }> Python def insertion_sort(bucket): for i in range(1, len(bucket)): key = bucket[i] j = i - 1 while j>= 0 et bucket[j]> clé : bucket[j + 1] = bucket[j] j -= 1 bucket[j + 1] = clé def bucket_sort(arr) : n = len(arr) buckets = [[] for _ in range(n)] # Placer les éléments du tableau dans différents buckets pour num in arr : bi = int(n * num) buckets[bi].append(num) # Trier les buckets individuels en utilisant le tri par insertion pour le bucket dans les buckets : insertion_sort (bucket) # Concaténer tous les buckets dans arr[] index = 0 pour bucket dans buckets : pour num dans bucket : arr[index] = num index += 1 arr = [0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434] bucket_sort (arr) print('Le tableau trié est :') print(' '.join(map(str, arr)))> C# using System; using System.Collections.Generic; class Program { // Insertion sort function to sort individual buckets static void InsertionSort(Listseau) { pour (int je = 1; je< bucket.Count; ++i) { float key = bucket[i]; int j = i - 1; while (j>= 0 && bucket[j]> clé) { bucket[j + 1] = bucket[j]; j--; } seau[j + 1] = clé ; } } // Fonction pour trier arr[] de taille n à l'aide du tri par bucket static void BucketSort(float[] arr) { int n = arr.Length; // 1) Créer une liste de n buckets vides[] seaux = nouvelle liste[n] ; pour (int je = 0; je< n; i++) { buckets[i] = new List(); } // 2) Placez les éléments du tableau dans différents compartiments pour (int i = 0; i< n; i++) { int bi = (int)(n * arr[i]); buckets[bi].Add(arr[i]); } // 3) Sort individual buckets using insertion sort for (int i = 0; i < n; i++) { InsertionSort(buckets[i]); } // 4) Concatenate all buckets into arr[] int index = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < buckets[i].Count; j++) { arr[index++] = buckets[i][j]; } } } // Driver program to test above function static void Main(string[] args) { float[] arr = { 0.897f, 0.565f, 0.656f, 0.1234f, 0.665f, 0.3434f }; BucketSort(arr); Console.WriteLine('Sorted array is:'); foreach (float num in arr) { Console.Write(num + ' '); } } }> Javascript function insertionSort(bucket) { for (let i = 1; i < bucket.length; ++i) { let key = bucket[i]; let j = i - 1; while (j>= 0 && bucket[j]> clé) { bucket[j + 1] = bucket[j]; j--; } seau[j + 1] = clé ; } } function bucketSort(arr) { let n = arr.length; let buckets = Array.from({length: n}, () => []); // Place les éléments du tableau dans différents compartiments pour (soit i = 0; i< n; i++) { let bi = Math.floor(n * arr[i]); buckets[bi].push(arr[i]); } // Sort individual buckets using insertion sort for (let i = 0; i < n; i++) { insertionSort(buckets[i]); } // Concatenate all buckets into arr[] let index = 0; for (let i = 0; i < n; i++) { for (let j = 0; j < buckets[i].length; j++) { arr[index++] = buckets[i][j]; } } } let arr = [0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434]; bucketSort(arr); console.log('Sorted array is:'); console.log(arr.join(' '));> Sortir
Sorted array is 0.1234 0.3434 0.565 0.656 0.665 0.897>
Analyse de la complexité de l'algorithme de tri par compartiment :
Complexité temporelle : Sur2),
- Si nous supposons que l'insertion dans un compartiment prend un temps O(1), alors les étapes 1 et 2 de l'algorithme ci-dessus prennent clairement un temps O(n).
- Le O(1) est facilement possible si nous utilisons une liste chaînée pour représenter un compartiment.
- L'étape 4 prend également un temps O(n) car il y aura n éléments dans tous les compartiments.
- La principale étape à analyser est l'étape 3. Cette étape prend également un temps O(n) en moyenne si tous les nombres sont uniformément distribués.
Espace auxiliaire : O(n+k)
