Zéros d'un polynôme sont ces valeurs réelles, imaginaires ou complexes lorsqu'elles sont placées dans le polynôme au lieu d'une variable, le résultat devient zéro (comme son nom l'indique également zéro). Les polynômes sont utilisés pour modéliser certains phénomènes physiques se produisant dans la vie réelle, ils sont très utiles pour décrire mathématiquement des situations.

Les zéros d'un polynôme sont toutes les valeurs x qui rendent le polynôme égal à zéro. Les zéros d’un polynôme nous renseignent sur les abscisses à l’origine du graphique du polynôme. Dans cet article, nous discuterons de les zéros d'un polynôme, comment les trouver, le théorème des facteurs, etc.

Table des matières

• Que sont les zéros des polynômes ?
• Zéros de la formule polynomiale
• Comment trouver le zéro d’un polynôme ?
• Pour le polynôme linéaire
• Pour le polynôme quadratique
• Pour le polynôme cubique
• Théorème des facteurs
• Relation entre les zéros et le coefficient
• Relation entre les zéros et le coefficient pour l'équation quadratique
• Relation entre les zéros et le coefficient pour l'équation cubique
• Former une équation avec des zéros de polynôme
• Zéros dans le graphique des polynômes
• Théorème fondamental de l'algèbre linéaire
• Multiplicité d'une racine
• Articles liés aux zéros du polynôme
• Exemples de problèmes sur les zéros d'un polynôme
• Problèmes pratiques sur les zéros du polynôme

Que sont les zéros des polynômes ?

Pour un polynôme P(x), nous disons que x = a est le zéro du polynôme si P(a) = 0, et tous ces zéros d'un polynôme sont communément appelés zéros d'un polynôme. Par exemple, considérons f(x) = 3x – 12. Maintenant, mettons x = 4 dans le polynôme, c'est-à-dire f(4) = 3×4 – 12 = 0. Ainsi, x = 4 est un zéro du polynôme f( x) = 3x – 12.

Exemple : Pour f(x) = x ³ – 6x ² + 11x – 6, x = 1 est-il nul ?

Solution:

Pour vérifier si si x = 1 est zéro de f(x) = x³– 6x²+ 11x – 6 ou pas, mettre x = 1 dans (x)

f(1) = (1)³– 6×(1)²+ 11×(1) – 6

⇒ f(1) = 1 – 6 + 11 – 6 = 12 -12 = 0

Ainsi, x = 1 est un zéro de f(x).

Zéros de la formule polynomiale

Pour un polynôme linéaire de forme ax + b, son zéro est donné par x = -b/a.

Pour un polynôme quadratique de forme hache²+ bx + c, son zéro est donné par x = {- b ± √D}/2a où D est le Discriminant donné par b²– 4ac.

Comment trouver le zéro d’un polynôme ?

Nous pouvons trouver les zéros du polynôme pour différents types de polynômes en utilisant diverses méthodes décrites ci-dessous.

• Pour le polynôme linéaire
• Pour le polynôme quadratique
• Pour le polynôme cubique

Pour le polynôme linéaire

Pour les polynômes linéaires, trouver zéro est le plus simple de tous. car il n'y a qu'un seul zéro et cela peut également être calculé par simple réarrangement du polynôme après le polynôme d'équivalence à 0.

Par exemple, trouvez zéro pour le polynôme linéaire f(x) = 2x – 7.

Solution:

Pour trouver le zéro de f(x), assimilez f(x) à 0.

⇒ 2x – 7 = 0

⇒ 2x = 7

⇒ x = 7/2

Pour le polynôme quadratique

Il existe différentes méthodes pour trouver les racines ou les zéros d'un polynôme quadratique, comme diviser le terme moyen, une formule quadratique également connue sous le nom de formule Shree Dharacharya, et compléter le carré qui est quelque peu similaire à la formule quadratique, comme vient la formule quadratique. à partir de la complétion du carré pour l’équation quadratique générale.

En savoir plus sur résoudre des équations quadratiques ou des polynômes et comment les résoudre. Les exemples suivants montrent en détail la méthode permettant de trouver les zéros des polynômes quadratiques.

Exemple 1 : Découvrez les zéros pour P(x) = x ² + 2x – 15.

Répondre:

X²+ 2x – 15 = 0

⇒x²+ 5x – 3x – 15 = 0

⇒ x(x + 5) – 3(x + 5) = 0

⇒ (x – 3) (x + 5) = 0

⇒ x = 3, -5

Exemple 2 : Trouver les zéros pour P(x) = x ² – 16x + 64.

Répondre:

X²– 16x + 64 = 0

En comparaison avec la hache²+ bx + c = 0,

nous obtenons a = 1, b = -16 et c = 64.

Ainsi,

⇒ x = 8, 8

Pour le polynôme cubique

Pour trouver les zéros du cube, il existe de nombreuses façons, telles que le théorème de la racine rationnelle et la division longue. Une méthode pour trouver les racines d’un polynôme cubique ou de tout polynôme de degré supérieur est la suivante :

Étape 1: Utilisez le théorème des racines rationnelles pour trouver les racines possibles. c'est-à-dire que si un polynôme a une racine rationnelle, il doit s'agir de la division de p/q, où p est la constante entière et q est le coefficient dominant.

Étape 2: Après avoir trouvé une racine, divisez le polynôme avec le facteur formé par cette racine en utilisant une division longue et écrivez le polynôme comme un produit du quotient et du dividende.

Étape 3: Si le quotient est une expression quadratique, résolvez-le par les méthodes mentionnées ci-dessus pour les polynômes quadratiques. S'il ne s'agit pas d'un polynôme de degré 2, répétez les étapes 1 et 2 jusqu'à ce que le quotient devienne un polynôme de degré 2.

Étape 4: Le résultat de l’étape 3 correspond aux facteurs requis, et en assimilant le facteur à 0, nous pouvons trouver les zéros du polynôme.

Exemple : Trouver les zéros du polynôme cubique p(x) = x ³ + 2x ² – 5x – 6.

Solution:

p(x) = x³+ 2x²– 5x – 6

Comme p/q = -6

Par théorème des racines rationnelles, toutes les racines rationnelles possibles du polunôme sont des diviseurs de p/q.

Ainsi, diviseurs = ±1, ±2, ±3, ±6

x = -1, dans p(x), on obtient

p(-1) = (-1)³+ 2(-1)²– 5(-1) – 6

acteur de cinéma vijay

⇒ p(-1) = -1 + 2 + 5 – 6 = 0

Ainsi, par le théorème des facteurs, x + 1 est le facteur de p(x).

Ainsi, x³+ 2x²– 5x – 6 = (x+1)(x²+x – 6)

⇒x³+ 2x²– 5x – 6 = (x+1)(x-2)(x+3)

Pour les zéros, p(x) = 0,

Les zéros de p(x) sont x = -1, x = 2 et x = -3.

Théorème des facteurs

Pour le polynôme P(x), le théorème des facteurs stipule que si x = a est zéro de P(X) si x – a est un facteur de P(x). c'est-à-dire que les deux conditions suivantes devraient être vraies.

• Si a est un zéro de P(x) alors x−a sera un facteur de P(x)
• Si x−a est un facteur de P(x) alors a sera un zéro de P(x)

Cela peut être vérifié en regardant les exemples précédents. Le théorème des facteurs peut conduire à des résultats intéressants, qui sont les suivants :

Résultat 1 : Si P(x) est un polynôme de degré n et r est un zéro de P(x) alors P(x) peut s'écrire sous la forme suivante,

P(x) = (x – r) Q(x)

Où Q(x) est un polynôme de degré n-1 et peut être découvert en divisant P(x) par (x – r).

Résultat 2 : Si P(x) = (x-r)Q(x) et x = t est un zéro de Q(x) alors x = t sera également un zéro de P(x).

Pour vérifier le fait ci-dessus,

Disons que t est nul Q(x), ce qui signifie Q(t) = 0.

On sait que r est un zéro du polynôme P(x), où P(x) = (x – r) Q(x),

Il faut donc vérifier si x = t est aussi un zéro de P(x), mettons x = t dans P(x)

⇒ P(t) = (t – r) Q(t) = 0

Donc, x = t est aussi un zéro P(x).

Par conséquent, prouvé.

Relation entre les zéros et le coefficient

La relation entre les zéros et le coefficient des équations quadratique et cubique est discutée ci-dessous.

Relation entre les zéros et le coefficient pour l'équation quadratique

Pour une équation quadratique de la forme hache²+ bx + c = 0, si les deux zéros de l'équation quadratique sont α et β, alors

• Somme de racine = α + β = -b/a
• Produit de racines = α × β = c/a

Relation entre les zéros et le coefficient pour l'équation cubique

Si α, β et γ sont la racine du polynôme cubique axe³+ boîte²+ cx + d = 0, alors la relation entre ses zéros et ses coefficients est donnée comme suit :

• a + b + c = -b/a
• α × β × γ = -d/a
• αβ + αγ + βγ = c/a

Former une équation avec des zéros de polynôme

• Pour un polynôme quadratique avec des zéros α et β, le polynôme quadratique est donné par

X ² – (a + b)x + ab .

• Pour un polynôme cubique avec trois zéros α, β et γ, le polynôme cubique est donné par

X ³ – (une + b + c )x ² + (ab + ag + bg)x – abg

Zéros dans le graphique des polynômes

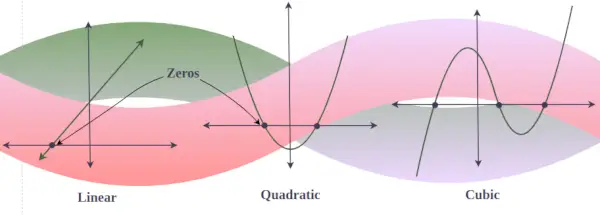
Dans le graphique de tout polynôme y = f(x), les zéros réels sont le point pour lequel le graphique coupe ou touche l'axe des x. (car un graphique avec un zéro imaginaire ne coupe jamais l'axe des x). En d'autres termes, s'il y a 3 solutions réelles d'un polynôme cubique, alors le graphique de ce polynôme cubique coupe l'axe des x trois fois, mais s'il n'y a qu'une seule solution réelle pour un polynôme cubique, alors son graphique ne coupe que l'axe des x. une fois.

Théorème fondamental de l'algèbre linéaire

Si P(x) est un polynôme de degré n alors P(x) aura exactement n zéros, dont certains peuvent se répéter.

Cela signifie que si nous listons tous les zéros et listons chacun k fois lorsque k est sa multiplicité. Nous aurons exactement n nombres dans la liste. Cela peut être utile car cela peut nous donner une idée du nombre de zéros qui devraient figurer dans un polynôme. Nous pouvons donc arrêter de chercher des zéros une fois que nous avons atteint le nombre de zéros requis.

Multiplicité d'une racine

Supposons que nous ayons un polynôme P(x) = 0 qui se factorise en,

P(x) = (x – r) ^k (x – une) ^m

Si r est un zéro d'un polynôme et que l'exposant de son terme qui a produit la racine est k alors on dit que r a multiplicité k . Les zéros avec une multiplicité de 1 sont souvent appelés simple les zéros et les zéros de multiplicité 2 sont appelés racines doubles du polynôme.

Exemple : P(x) est un polynôme de degré 5, qui a été factorisé pour vous. Énumérez les racines et leur multiplicité.

P(x) = 5x ⁵ −20x ⁴ +5x ³ +50x ² −20x−40=5(x+1) ² (x−2) ³

Solution:

Étant donné, P(x) = 5(x+1)²(x−2)³

⇒ P(x) = 5(x+1)(x+1)(x+1)(x−2)(x−2)

Pour trouver des zéros, P(x) = 0

⇒ x = -1, -1, 2, 2, 2

Notez que -1 apparaît deux fois comme zéro, donc sa multiplicité est 2 tandis que la multiplicité du zéro 2 est 3.

Articles liés aux zéros du polynôme

• Polynôme
• Racines de l'équation quadratique
• Expression algébrique

Exemples de problèmes sur les zéros d'un polynôme

Problème 1 : étant donné que x = 2 est un zéro de P(x) = x ³ +2x ² −5x−6. Trouvez les deux autres zéros.

Solution:

À partir du théorème fondamental que nous avons étudié plus tôt, nous pouvons dire que P(x) aura 3 zéros car c’est un polynôme de trois degrés. L'un d'eux est x = 2.

On peut donc réécrire P(x),

P(x) = (x – 2) Q(x)

Pour trouver les deux autres zéros, nous devons connaître le Q(x).

Q(x) peut être découvert en divisant P(x) par (x-2).

Après division, le Q(x) s'avère être,

Q(x) = x²+4x +3

Les deux zéros restants peuvent être découverts à partir de là,

Q(x) = x²+ 3x + x + 3

⇒ x(x + 3) + 1(x + 3)

⇒ (x + 1) (x + 3)

Q(x) = 0,

x = -1, -3

Ainsi, les deux autres zéros sont x = -1 et x = -3.

Problème 2 : Étant donné que x = r est un zéro d'un polynôme, découvrez les autres zéros du polynôme.

P(x) = x ³ -6x ² −16x ; r = −2

Solution:

On sait que x = -2 est un zéro,

Ainsi, P(x) peut être réécrit sous la forme P(x) = (x + 2) Q(x) {En utilisant l'algorithme de division}

Maintenant, pour trouver Q(x), nous faisons la même chose que dans la question précédente, nous divisons P(x) par (x + 2).

On a,

Q(x) = x²– 8x

Maintenant, pour trouver les deux autres zéros, factorisons Q(x)

Q(x) = x (x – 8) = 0

Donc les zéros sont x = 0, 8.

Ainsi, nous avons trois zéros, x = -2, 0, 8.

Problème 3 : Trouver les zéros du polynôme, 4x ³ -3x ² -25x-6 = 0

Solution:

Astuce pour résoudre des équations polynomiales de degré 3,

Trouvez le plus petit entier pouvant donner à la valeur polynomiale 0, commencez par 1,-1,2, et ainsi de suite…

nous constatons que pour x = -2, nous obtenons que la valeur de l'expression soit nulle.

L’une des racines est donc -2.

Selon le théorème des facteurs, si a est l'un des zéros du polynôme, donc (x-a) est le facteur du polynôme donné.

Ainsi, suite à cela {x – (-2)} = (x+2) est un facteur pof supérieur au polynôme.

Nous obtenons une équation quadratique et des zéros sont déjà là.

(4x²-11x-3)(x+2) = 0

Factoriser l'équation quadratique,

(4x²-12x+x-3)(x+2) = 0

[4x(x-3)+1(x-3)](x+2) = 0

(4x+1)(x-3)(x+2) = 0

x = -2, x = 3, x = -1/4

Problème 4 : Trouver les zéros du polynôme, 4x ⁶ – 16x ⁴ = 0

Solution:

Le polynôme a jusqu'au degré 6, il existe donc 6 zéros du polynôme.

4x⁴(X²-4) = 0

4x⁴(X²-2²) = 0

4x⁴[(x+2)(x-2)] = 0

Donc x= 0, 0, 0, 0, 2, -2

Problème 5 : Trouver les zéros de la fonction polynomiale f(x) = x ³ – 2x ² – 5x + 6

Solution:

Pour trouver les zéros de ce polynôme, nous définissons f(x) = 0 et résolvons pour x :

f(x) = x³– 2x²– 5x + 6 = 0

Comme d/a = 6

Par le théorème des racines rationnelles, toutes les racines rationnelles possibles du polunôme sont,

Diviseurs de d/a = ±1, ±2, ±3, ±6

x = 1, dans p(x), on obtient

f(1) = (1)³– 2(1)²– 5(1) – 6

f(-1) = 1 – 2 – 5 + 6 = 0

Ainsi, par le théorème des facteurs, x – 1 est le facteur de p(x).

Ainsi, x³+ 2x²– 5x – 6 = (x-1)(x²-x – 6)

X³+ 2x²– 5x – 6 = (x-1)(x+2)(x-3)

Pour les zéros, p(x) = 0,

Les zéros de p(x) sont x = 1, x = -2 et x = 3.

Problèmes pratiques sur les zéros du polynôme

1. Trouver tous les zéros du polynôme f(x) = x ³ – 6x ² + 11x – 6

2. Déterminer tous les zéros du polynôme g(x) = 2x ⁴ – 7x ³ + 3x ² + 4x – 4

3. Trouvez les zéros du polynôme h(x) = x ⁵ – 3x ⁴ + 2x ³ – 6x ² + x + 2

4. Déterminer tous les zéros du polynôme p(x) = 3x ⁴ – 16x ³ + 18x ² + 16x – 12.

FAQ sur les zéros du polynôme

Que sont les zéros d’un polynôme ?

Ces valeurs réelles, car la valeur du polynôme devient 0, c'est-à-dire que si p(x) est un polynôme et que p(a) = 0, alors x = a est le zéro de p(x).

Comment trouver les zéros d'un polynôme ?

Il existe différentes méthodes permettant à différents polynômes de trouver des zéros, par exemple pour le déversement quadratique du moyen terme et la formule quadratique. Pour le réarrangement linéaire et simple des variables et pour le cubique, nous utilisons une combinaison du théorème de la racine rationnelle, de la division longue, du théorème des facteurs et du théorème des restes.

Un polynôme peut-il avoir plus d’un zéro ?

Oui, un polynôme peut avoir plus d'un zéro, en fait, le polynôme de n degrés peut avoir au plus n zéros réels.

Quelle est la multiplicité d’un zéro d’un polynôme ?

Dans le processus de factorisation, un facteur ou un zéro d'un polynôme est suivi un certain nombre de fois d'un facteur ou d'un zéro, c'est ce qu'on appelle la multiplicité de cette racine.

jframe

Qu'est-ce que le théorème fondamental de l'algèbre ?

Le théorème fondamental des états algébriques Si P(x) est un polynôme de degré n alors P(x) aura exactement n zéros, dont certains peuvent se répéter.

Un polynôme de degré n a-t-il toujours n racines réelles ?

Non, un polynôme de degré n n’a pas toujours n racines réelles, car certaines racines peuvent être des nombres imaginaires ou complexes.

Quel est le degré du polynôme zéro ?

Le degré du polynôme nul est nul.