Le volume d'une pyramide triangulaire est trouvé à l'aide de la formule V = 1/3A.H . Une pyramide triangulaire, également connue sous le nom de tétraèdre, est un type de pyramide avec une base triangulaire et trois faces triangulaires qui se rejoignent en un seul point appelé sommet.

Dans cet article, nous découvrirons en détail la définition de la pyramide, la définition de la pyramide triangulaire, la formule de la pyramide triangulaire, des exemples et d'autres.

Table des matières

• Qu'est-ce qu'une pyramide ?
• Définition de la pyramide triangulaire
• Formule de pyramide triangulaire
• Superficie d'une pyramide triangulaire
• Volume d'une pyramide triangulaire

Qu'est-ce qu'une pyramide ?

UN pyramide est classé en différents types en fonction de la forme de la base, comme une pyramide triangulaire, une pyramide carrée, une pyramide pentagonale, une pyramide hexagonale, etc. Un sommet est un point de rencontre des surfaces latérales ou des faces latérales d'une pyramide. . La distance perpendiculaire entre le sommet d'une pyramide et le centre de sa base est la hauteur ou l'altitude d'une pyramide. Distance perpendiculaire entre le sommet et la base de la hauteur inclinée de la surface latérale d'une pyramide.

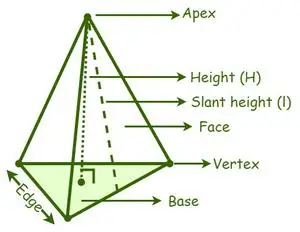
Pyramide

Définition de la pyramide triangulaire

Pyramide triangulaire est une pyramide qui a pour base un triangle. Il est également connu sous le nom de tétraèdre et possède trois faces de forme triangulaire et une base triangulaire, la base triangulaire pouvant être scalaire, isocèle ou un triangle équilatéral. Une pyramide triangulaire est en outre classée en trois types, à savoir une pyramide triangulaire régulière, une pyramide triangulaire irrégulière et une pyramide triangulaire droite.

• Pyramide triangulaire régulière : Une pyramide triangulaire dont les quatre faces sont des triangles équilatéraux est appelée pyramide triangulaire régulière. La pyramide étant constituée de triangles équilatéraux, la mesure de tous ses angles internes est de 60°.

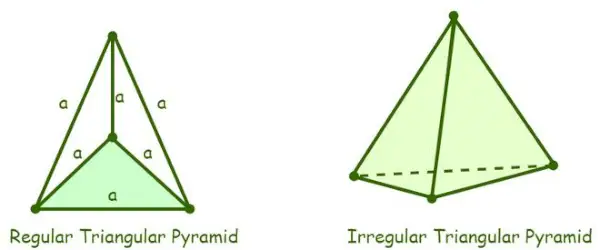
Définition de la pyramide triangulaire

• Pyramide triangulaire irrégulière : Une pyramide triangulaire irrégulière est une pyramide dont les bords de la base ne sont pas égaux, c'est-à-dire que la base d'une pyramide triangulaire irrégulière est soit un triangle scalène, soit un triangle isocèle. Toutes les pyramides triangulaires sont considérées comme des pyramides triangulaires régulières, à moins qu'une pyramide triangulaire ne soit spécifiquement mentionnée comme étant irrégulière.

• Pyramide triangulaire droite : Une pyramide triangulaire rectangle est une pyramide dont la base est un triangle rectangle et dont le sommet est aligné au-dessus du centre de la base.

Formule de pyramide triangulaire

Il existe deux formules pour une pyramide triangulaire : la surface d'une pyramide triangulaire et le volume d'une pyramide triangulaire.

• Superficie d'une pyramide triangulaire
  • Surface latérale d'une pyramide triangulaire
  • Superficie totale d'une pyramide triangulaire
• Volume d'une pyramide triangulaire

Superficie d'une pyramide triangulaire

La surface d'une pyramide a deux types de surfaces, à savoir : la surface latérale et la surface totale, où la surface d'une pyramide est la somme des surfaces des surfaces latérales, ou faces latérales, et de la surface de base. d'une pyramide.

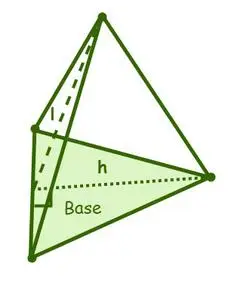
Superficie d'une pyramide triangulaire

Surface latérale d'une pyramide triangulaire

La surface latérale d'une pyramide triangulaire est calculée à l'aide de la formule :

Surface latérale d'une pyramide triangulaire (LSA) = ½ × périmètre × hauteur inclinée

Superficie totale d'une pyramide triangulaire

La surface totale d'une pyramide (TSA) = Surface latérale de la pyramide + Aire de la base

Donc, TSA = ½ × périmètre × hauteur inclinée + ½ × base × hauteur

Superficie totale d'une pyramide triangulaire (TSA) = ½ × P × l + ½ bh

où,

• P. est le périmètre de la base
• je est la hauteur inclinée de la pyramide
• b est la base du triangle à la base
• h est la hauteur de la pyramide

Volume d'une pyramide triangulaire

Le volume d'une pyramide est l'espace total compris entre toutes les faces d'une pyramide. Le volume d'une pyramide est généralement représenté par la lettre V, et sa formule est égale au tiers du produit de l'aire de base et de la hauteur de la pyramide.

La formule du volume d’une pyramide est donnée comme suit :

Volume d'une pyramide triangulaire = 1/3 × surface de base × hauteur

V = 1/3 × AH unités cubes

où,

• DANS est le volume de la pyramide
• UN est l'aire de la base d'une pyramide
• H est la hauteur ou l'altitude d'une pyramide

La formule du volume d'une pyramide triangulaire régulière est donnée comme suit

Volume de la pyramide triangulaire régulière = a ³ /6√2 unités cubes

Où un isLongueur des arêtes

Article lié à la pyramide triangulaire :

• Pyramide rectangulaire
• Pyramide carrée
• Pyramide Pentagonale
• Pyramide hexagonale
• Volume d'une formule pyramidale
• Superficie d'une formule pyramidale

Exemples de formule de pyramide triangulaire

Exemple 1 : Déterminer le volume d'une pyramide triangulaire dont l'aire de base et la hauteur sont de 50 cm ² et 12 cm, respectivement.

Solution:

Compte tenu des données,

• Aire de la base triangulaire = 100 cm²
• Hauteur de la pyramide = 12 cm

Nous savons que,

Volume d'une pyramide triangulaire (V) = 1/3 × Aire de la base triangulaire × Hauteur

caractère java en chaîne

H = 1/3 × 50 × 12 = 200 cm³

Le volume de la pyramide triangulaire donnée est donc de 200 cm.³.

Exemple 2 : Trouvez la surface totale d'une pyramide triangulaire régulière lorsque la longueur de chaque bord est de 8 pouces.

Solution:

Compte tenu des données,

• Longueur de chaque bord d'une pyramide triangulaire régulière (a) = 8 pouces

Nous savons que,

Superficie totale d'une pyramide triangulaire régulière = √3a²

⇒ TSA = √3 × 8²

= 64√3 = 110,851 pouces carrés

Par conséquent, la superficie totale d’une pyramide triangulaire régulière est de 110,851 pouces carrés.

Exemple 3 : Déterminer le volume d'une pyramide triangulaire régulière lorsque la longueur du bord est de 10 cm.

Solution:

Compte tenu des données,

• Longueur de chaque arête d'une pyramide triangulaire régulière (a) = 10 cm

Nous savons que,

Volume d'une pyramide triangulaire régulière = a³/6√2

⇒ V = (10)³/6√2

= 1000/6√2 = 117,85 cm³

Par conséquent, le volume d’une pyramide triangulaire régulière est de 117,85 mètres cubes. cm.

Exemple 4 : Trouvez la hauteur inclinée de la pyramide triangulaire si sa surface latérale est de 600 pouces carrés et le périmètre de la base est de 60 pouces.

Solution:

Compte tenu des données,

• Superficie latérale = 600 po²
• Périmètre de la base = 60 pouces

Nous savons que,

Surface latérale = ½ × périmètre × hauteur inclinée

600 = ½ × 60 × l

l = 600/30 = 20 pouces

Par conséquent, la hauteur inclinée de la pyramide donnée est de 20 pouces.

Exemple 5 : Déterminez la superficie totale d'une pyramide triangulaire dont la superficie de la base est de 28 cm², le périmètre du triangle est de 18 cm et la hauteur inclinée de la pyramide est de 20 cm.

Solution:

Compte tenu des données,

• Surface de la base triangulaire = 28 cm²
• Hauteur d'inclinaison (l) = 20 cm
• Périmètre (P) = 18 cm

Nous savons que,

Surface totale (TSA) d'une pyramide triangulaire = ½ × périmètre × hauteur inclinée + Surface de base

⇒ TSA = ½ × 18 × 20 + 28

= 180 + 28 = 208 cm²

La superficie totale de la pyramide donnée est donc de 208 cm².

Problèmes pratiques sur la formule de la pyramide triangulaire

T1. Étant donné une pyramide triangulaire ayant une aire de base de 15 unités carrées et une hauteur de 10 unités, quel est le volume de la pyramide ?

Q2. Étant donné une pyramide triangulaire régulière dont chaque bord de la base triangulaire équilatérale mesure 6 unités, quelle est la superficie totale de la pyramide ?

Q3. Étant donné une pyramide triangulaire régulière dont chaque bord de la base triangulaire équilatérale mesure 4 unités et une hauteur de 5 unités, quels sont le volume et la surface totale de la pyramide ?

Q4. Si les longueurs des côtés de la base d'une pyramide triangulaire sont de 3 unités, 4 unités et 5 unités, et que la hauteur de la pyramide est de 12 unités, quel est le volume de la pyramide ?

Q5. Pour une pyramide triangulaire ayant une base en forme de triangle rectangle avec des pattes de 3 unités et 4 unités et une hypoténuse de 5 unités, quelle est la superficie totale si la hauteur de la pyramide de la base au sommet est de 10 unités ?

FAQ sur la formule de la pyramide triangulaire

Quelle est la définition d’une pyramide triangulaire ?

Une pyramide triangulaire est une forme géométrique qui a une base triangulaire et trois faces triangulaires ayant un sommet commun.

Combien de faces et de sommets possède une pyramide triangulaire ?

La pyramide triangulaire a quatre faces et quatre sommets. Un sommet est commun aux trois faces de la pyramide.

Quelle est la formule de base d’une pyramide ?

Les formules de base d'une pyramide sont :

• LSA = ½ × périmètre × hauteur inclinée
• TSA = ½ × P × l + ½ bh
• V = 1/3 × AH

Quels sont les types de pyramides triangulaires ?

Il existe trois types de pyramides triangulaires :

• Pyramide triangulaire régulière
• Pyramide triangulaire irrégulière
• Pyramide triangulaire à angle droit

Qu'est-ce que la formule des triangles ?

La formule pour l’aire d’un triangle est :

• (Zone)A = 1/2 × b × h