Une fonction récursive peut être définie comme une routine qui s'appelle directement ou indirectement.

En d’autres termes, une fonction récursive est une fonction qui résout un problème en résolvant des instances plus petites du même problème. Cette technique est couramment utilisée en programmation pour résoudre des problèmes qui peuvent être décomposés en sous-problèmes plus simples et similaires.

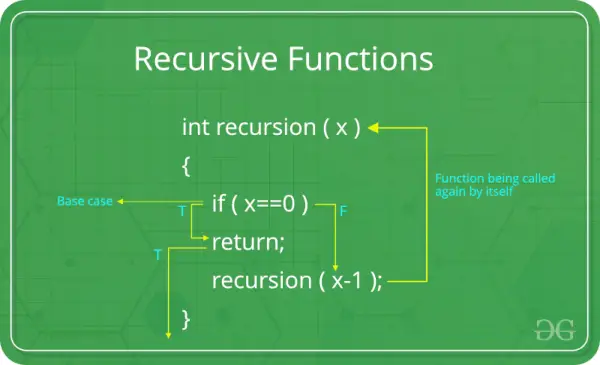
Besoin d'une fonction récursive :

Une fonction récursive est une fonction qui résout un problème en résolvant des instances plus petites du même problème. Cette technique est souvent utilisée en programmation pour résoudre des problèmes qui peuvent être décomposés en sous-problèmes plus simples et similaires.

alphabet par chiffres

1. Résoudre des tâches complexes :

Les fonctions récursives divisent les problèmes complexes en instances plus petites du même problème, ce qui donne un code compact et lisible.

2. Diviser pour conquérir :

Les fonctions récursives conviennent aux algorithmes diviser pour régner tels que le tri par fusion et le tri rapide, diviser les problèmes en sous-problèmes plus petits, les résoudre de manière récursive et fusionner les solutions avec le problème d'origine.

3. Retour en arrière :

Le retour en arrière récursif est idéal pour explorer et résoudre des problèmes comme N-Queens et Sudoku.

4. Dynamique la programmation:

Les fonctions récursives résolvent efficacement les problèmes de programmation dynamique en résolvant des sous-problèmes et en combinant leurs solutions en une solution complète.

5. Arbre et structures graphiques :

Les fonctions récursives sont idéales pour travailler avec des structures arborescentes et graphiques, simplifiant les tâches de parcours et de reconnaissance de formes .

Comment écrire une fonction récursive :

Composants d'une fonction récursive :

Cas de base: Chaque fonction récursive doit avoir un cas de base. Le cas de base est le scénario le plus simple qui ne nécessite pas de récursivité supplémentaire. Il s'agit d'une condition de terminaison qui empêche la fonction de s'appeler indéfiniment. Sans un cas de base approprié, une fonction récursive peut conduire à une récursion infinie.

Java version Linux

Cas récursif : Dans le cas récursif, la fonction s'appelle avec les arguments modifiés. C'est l'essence de la récursivité : résoudre un problème plus vaste en le décomposant en instances plus petites du même problème. Le cas récursif doit se rapprocher du cas de base à chaque itération.

Prenons l'exemple de factorielle du nombre :

Dans cet exemple, le cas de base est lorsque n est 0 , et la fonction renvoie 1 . Le cas récursif se multiplie n avec le résultat de la fonction appelée en paramètre n – 1 . Le processus se poursuit jusqu'à ce que le scénario de base soit atteint.

Il est essentiel de s'assurer que la fonction récursive a un cas de base correct et que les appels récursifs mènent au cas de base, sinon la procédure pourrait s'exécuter indéfiniment, entraînant un débordement de pile (dépassant la mémoire disponible allouée aux appels de fonction).

Ci-dessous l'implémentation de la factorielle d'un nombre :

#include  using namespace std; // Recursive Function to calculate Factorial of a number int factorial(int n) {  // Base case  if (n == 0) {  return 1;  }  // Recursive case  return n * factorial(n - 1); } // Driver Code int main() {  int n = 4;  cout << 'Factorial of ' << n  << ' is:' << factorial(n);  return 0; }>

import java.util.Scanner; public class Factorial {  // Recursive Function to calculate the factorial of a number  static int factorial(int n) {  // Base case: If n is 0, the factorial is 1.  if (n == 0) {  return 1;  }  // Recursive case: Calculate the factorial by multiplying n with the factorial of (n - 1).  return n * factorial(n - 1);  }  public static void main(String[] args) {  int n = 4;  // Calculate and print the factorial of n.  int result = factorial(n);  System.out.println('Factorial of ' + n + ' is: ' + result);  } }>

# Recursive Function to calculate Factorial of a number def factorial(n): # Base case if n == 0: return 1 # Recursive case return n * factorial(n - 1) # Driver Code if __name__ == '__main__': n = 4 print('Factorial of', n, 'is:', factorial(n))>

using System; class Program {  // Recursive Function to calculate Factorial of a number  static int Factorial(int n)  {  // Base case  if (n == 0)  {  return 1;  }  // Recursive case  return n * Factorial(n - 1);  }  // Driver Code  static void Main()  {  int n = 4;  Console.WriteLine('Factorial of ' + n + ' is: ' + Factorial(n));  } }>

// Function to calculate the factorial of a number using recursion function factorial(n) {  // Base case: If n is 0, the factorial is 1.  if (n === 0) {  return 1;  }  // Recursive case: Calculate the factorial by multiplying n with the factorial of (n - 1).  return n * factorial(n - 1); } // Main function function main() {  // Given number  let n = 4;  // Calculate the factorial of n.  let result = factorial(n);  // Print the result  console.log('Factorial of ' + n + ' is: ' + result); } // Call the main function main();>

Factorial of 4 is:24>

Complexité temporelle : Sur)
Espace auxiliaire : Sur)