Quadrant est défini comme une région de l'espace divisée en quatre parties égales par deux axes, à savoir l'axe X et l'axe Y dans le plan cartésien. Ces deux axes se croisent à 90 degrés et les quatre régions ainsi formées sont appelées quatre quadrants, à savoir le quadrant I, le quadrant II, le quadrant III et le quadrant IV.
Unix contre Windows
Dans cet article, nous explorerons les concepts essentiels du quadrant, notamment ce qu'est un quadrant, son aire, son graphique de quadrant, son plan cartésien, les conventions de signes dans le quadrant, l'abscisse et les coordonnées, ainsi que le tracé des points sur un quadrant.
Table des matières
- Que sont les quadrants du graphique ?
- Convention de signature dans les quadrants
- Tracer des points sur des quadrants
- Valeurs trigonométriques dans différents quadrants
Que sont les quadrants du graphique ?
Un quadrant est une zone désignée sur un plan cartesien , créé par l'intersection des axes X et Y. Dans ce plan, quatre quadrants sont formés, chacun ayant ses caractéristiques uniques. Le premier quadrant, en haut à droite, a des coordonnées x et y positives. Le deuxième quadrant, en haut à gauche, a des coordonnées x négatives et y positives, et ainsi de suite. Comprendre ces quadrants est essentiel pour localiser et interpréter les points sur le graphique, fournissant ainsi un moyen systématique de naviguer et d'analyser les coordonnées cartésiennes.
4 quadrants sur le plan de coordonnées
Le plan cartésien, formé par les axes X et Y, est divisé en quatre quadrants, chacun ayant des caractéristiques distinctes :
- Premier quadrant : Situées en haut à droite, les coordonnées x et y sont positives. Ce quadrant représente les points dans la partie supérieure droite du plan.
- Deuxième quadrant : Située en haut à gauche, la coordonnée x est négative et la coordonnée y est positive. Ce quadrant couvre les points de la partie supérieure gauche du plan.
- Troisième quadrant : Positionnées en bas à gauche, les coordonnées x et y sont négatives. Les points situés dans la zone inférieure gauche du plan tombent dans ce quadrant.
- Quatrième quadrant : En bas à droite, la coordonnée x est positive et la coordonnée y est négative. Ce quadrant comprend des points dans la partie inférieure droite du plan.
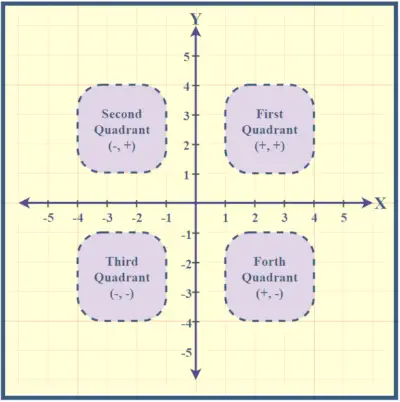
Les quadrants sont numérotés dans le sens inverse des aiguilles d'une montre, en partant du coin supérieur droit. Le point d'intersection des axes X et Y est appelé l'origine, avec des coordonnées (0,0), indiquant des valeurs nulles pour x et y. Comprendre ces quadrants permet de localiser les points dans le plan cartésien.
Qu’est-ce que l’Origine ?
Le point de départ sur un graphique, appelé origine et représenté par (0, 0), est l'endroit où l'axe des x horizontal et l'axe des y vertical se croisent. Cela signifie qu’à l’origine, les valeurs de x et y sont nulles. Il sert de point de référence pour localiser d'autres points sur le graphique. Dans l'image ajoutée ci-dessus, le point O montre l'origine.
Abscisse et ordonnée dans les quadrants
Dans les quatre quadrants, les nombres sont représentés par des paires (a, b), où « a » représente la coordonnée x et « b » la coordonnée y. Pour déterminer où se trouve un point sans tracer, faites attention aux signes de la coordonnée x (abscisse) et de la coordonnée y (ordonnée). Par exemple, si vous avez un point comme Q (3, -5), les signes (+ve, -ve) indiquent qu'il se trouve dans le quadrant IV.
L'abscisse montre la distance horizontale par rapport à l'axe Y. Une abscisse positive signifie vers la droite, et dans notre exemple, abscisse = 3 signifie aller à droite de l'origine le long de l'axe des x de 3 unités.
L'ordonnée indique la distance verticale à partir de l'origine. Une ordonnée négative signifie descendre de l’origine le long de l’axe y. Dans l'exemple, ordonnée = -5 signifie descendre de 5 unités.
Convention de signature dans les quadrants
Les conventions de signes dans les quadrants peuvent être facilement comprises à l'aide de l'image ajoutée ci-dessous,

Dans le plan XY, à mesure que nous nous déplaçons de gauche à droite le long de l’axe des x, la coordonnée x augmente. De même, le long de l’axe y, le déplacement de bas en haut entraîne une augmentation de la coordonnée y. Le plan XY est divisé en quatre quadrants, chacun avec des conventions de signes spécifiques pour les coordonnées x et y :
| Quadrant | coordonnée x | coordonnée y |
|---|---|---|
| 1er quadrant | Positif (+) | Positif (+) |
| 2e quadrant | Négatif (-) | Positif (+) |
| 3ème quadrant | Négatif (-) | Négatif (-) |
| 4ème quadrant | Positif (+) | Négatif (-) |
Par conséquent, les points du 1er quadrant ont des valeurs positives pour x et y, ceux du 2ème quadrant ont un x négatif et un y positif, le 3ème quadrant a des valeurs x et y négatives, et le 4ème quadrant a un x et un y positifs. un y négatif.
Tracer des points sur des quadrants
Dans un plan cartésien, les points sont identifiés par l'axe des x et l'axe des y. Ces points sont notés (a, b), où « a » est la coordonnée x (abscisse) et « b » est la coordonnée y (ordonnée). Pour positionner un point dans un quadrant, on considère les signes de ces coordonnées. Les valeurs de x et y représentent respectivement la distance entre le point et l'axe des x et l'axe des y.
Par exemple, tracez le point (2, -5) sur le plan cartésien. L'analyse du signe des coordonnées révèle que le point est dans le 4ème quadrant. Il sera à 2 unités de l'axe des x (vers la droite) et à 5 unités de l'axe des y (vers le bas), en utilisant l'origine comme point de référence.
Valeurs trigonométriques dans différents quadrants
Les valeurs de divers fonctions trigonométriques dans différents quadrants peut être appris en étudiant le tableau ajouté ci-dessous comme,
| Quadrant | Sans | Parce que | Donc | Cosécante | Sécante | Cotangente |
|---|---|---|---|---|---|---|
| 1er quadrant | + méthode de sous-chaîne en Java | + | + | + | + | + |
| 2e quadrant | + | – | + | + | – | – |
| 3ème quadrant | – | – | – | – | – | + |
| 4ème quadrant | – | – | – | – | + | – |
Dans le 1er quadrant, tous les rapports trigonométriques sont positifs. Dans le 2ème quadrant, Sinus et Cosecant sont positifs (+), tandis que Cosinus et Secant sont négatifs (-). Dans le 3ème quadrant, Tangente et Cotangente sont positives (+), tandis que Cosinus et Sécante sont négatives (-). Dans le 4ème quadrant, Sinus et Cosecant sont négatifs (-), tandis que Cosinus et Secant sont positifs (+).
En savoir plus,
- Géométrie coordonnée
- Lignes parallèles
- Formule de distance
Exemples résolus sur le quadrant
Exemple 1 : Tracez le point A (3, -4) et identifiez son quadrant.
Solution:
Le point A est situé aux coordonnées (3, -4). Puisque la coordonnée x est positive (3) et la coordonnée y est négative (-4), le point A se trouve dans le quadrant IV.
la classe abstraite peut-elle avoir un constructeur
Exemple 2 : Tracez le point P (-5, 2) et déterminez son quadrant
Solution:
Les coordonnées du point P sont (-5, 2). Pour déterminer le quadrant, nous examinons les signes des coordonnées x et y.
La coordonnée X est -5, indiquant une position à gauche de l'origine.
La coordonnée Y est 2, indiquant une position au-dessus de l'origine.
Par conséquent, puisque la coordonnée x est négative et la coordonnée y est positive, le point P est situé dans le quadrant II.
Le point P (-5, 2) est situé dans le quadrant II du plan cartésien.
Problèmes de pratique sur les quadrants
Problème 1 : Tracez le point (1, -1) et identifiez son quadrant.
Problème 2 : Trouvez trois points sur l'axe des x et déterminez leurs quadrants.
Problème 3 : Si un point se trouve sur l’axe y avec les coordonnées (0, -3), dans quel quadrant se trouve-t-il ?
Problème 4 : Localisez les points Q (2, 2), R (-2, -2) et S (0, 0) et vérifiez la colinéarité.
Problème 5 : Tracez le point (-4, -3) et expliquez dans quel quadrant il se situe.
FAQ sur les quadrants
1. Qu'est-ce qu'un quadrant en mathématiques ?
En mathématiques, un quadrant est l'une des quatre sections créées par l'intersection de deux lignes ou axes perpendiculaires. Ces axes sont généralement appelés axe x et axe y dans un système de coordonnées cartésiennes.
2. Comment s’appelle l’intersection de deux axes ?
L'intersection de deux axes dans un système de coordonnées cartésiennes s'appelle l'origine. Il est représenté par le point de rencontre des axes x et y, généralement noté (0,0).
3. Que sont les 4 quadrants ?
Les quatre quadrants sont les sections formées en divisant un plan de coordonnées cartésien en quatre parties égales. Ils sont appelés premier quadrant (Q1), deuxième quadrant (Q2), troisième quadrant (Q3) et quatrième quadrant (Q4).
4. Quel quadrant est positif ?
Le quadrant positif dans un système de coordonnées cartésiennes est le premier quadrant (Q1). Dans ce quadrant, les coordonnées x et y sont positives.
5. Quelle est l’utilisation des quadrants dans les graphiques ?
Les quadrants dans les graphiques fournissent un moyen systématique d'organiser et de localiser des points en fonction de leurs coordonnées. Ils aident à visualiser les relations entre les variables et à analyser les modèles dans les ensembles de données, facilitant ainsi l'interprétation des représentations graphiques.
6. Quel quadrant a les deux valeurs de coordonnées positives ?
Le premier quadrant (Q1) est le quadrant où les coordonnées x et y des points sont positives. C'est le seul quadrant avec les deux valeurs positives.
7. Quels sont les 4 quadrants d'un cercle ?
Le concept de quadrants n'est pas directement applicable aux cercles. Au lieu de cela, les cercles sont divisés en angles mesurés en degrés. Cependant, si l'on fait référence à des secteurs circulaires, on peut utiliser des termes comme premier secteur, deuxième secteur, troisième secteur et quatrième secteur, correspondant à différentes régions angulaires.
