• Les automates pushdown sont un moyen d'implémenter un CFG de la même manière que nous concevons DFA pour une grammaire normale. Un DFA peut mémoriser une quantité limitée d'informations, mais un PDA peut mémoriser une quantité infinie d'informations.
• Les automates pushdown sont simplement un NFA augmenté d'une « mémoire de pile externe ». L'ajout d'une pile est utilisé pour fournir une capacité de gestion de la mémoire dernier entré, premier sorti aux automates Pushdown. Les automates pushdown peuvent stocker une quantité illimitée d'informations sur la pile. Il peut accéder à une quantité limitée d'informations sur la pile. Un PDA peut pousser un élément en haut de la pile et retirer un élément du haut de la pile. Pour lire un élément dans la pile, les éléments supérieurs doivent être retirés et sont perdus.
• Un PDA est plus puissant qu'un FA. Toute langue pouvant être acceptable par FA peut également être acceptable par PDA. PDA accepte également une classe de langue qui ne peut même pas être acceptée par FA. Ainsi, le PDA est bien supérieur au FA.

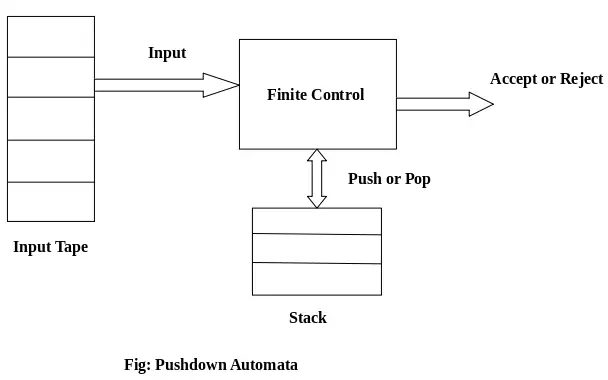
Composants du PDA :

Bande d'entrée : La bande d'entrée est divisée en plusieurs cellules ou symboles. La tête de saisie est en lecture seule et ne peut se déplacer que de gauche à droite, un symbole à la fois.

Contrôle fini : Le contrôle fini a un pointeur qui pointe vers le symbole actuel qui doit être lu.

Empiler: La pile est une structure dans laquelle nous pouvons pousser et supprimer les éléments d’un seul côté. Il a une taille infinie. Dans PDA, la pile est utilisée pour stocker temporairement les éléments.

Définition formelle du PDA :

Le PDA peut être défini comme un ensemble de 7 composants :

Question : l'ensemble fini des états

∑ : l'ensemble d'entrée

C : un symbole de pile qui peut être poussé et retiré de la pile

q0 : l'état initial

chaîne java de concaténation

AVEC: un symbole de départ qui est en Γ.

F: un ensemble d'états finaux

d: fonction de mappage qui est utilisée pour passer de l’état actuel à l’état suivant.

Description instantanée (ID)

L'ID est une notation informelle de la façon dont un PDA calcule une chaîne d'entrée et décide que la chaîne est acceptée ou rejetée.

Une description instantanée est un triplet (q, w, α) où :

q décrit l'état actuel.

Dans décrit l'entrée restante.

exemple de sous-chaîne Java

un décrit le contenu de la pile, en haut à gauche.

Notation du tourniquet :

Le signe ⊢ décrit la notation du tourniquet et représente un mouvement.

Le signe ⊢* décrit une séquence de mouvements.

Par exemple,

(p, b, T) ⊢ (q, w, α)

Dans l'exemple ci-dessus, lors d'une transition de l'état p à q, le symbole d'entrée « b » est consommé et le haut de la pile « T » est représenté par une nouvelle chaîne α.

Exemple 1:

Concevoir un PDA pour accepter une langueⁿb²ⁿ.

Solution: Dans cette langue, n nombre de a doit être suivi de 2n nombre de b. Par conséquent, nous appliquerons une logique très simple : si nous lisons un seul « a », nous placerons deux a sur la pile. Dès que nous lisons «b», alors pour chaque «b», un seul «a» devrait être retiré de la pile.

tranche java

L'ID peut être construit comme suit :

 δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa) 

Maintenant, lorsque nous lirons b, nous changerons l'état de q0 à q1 et commencerons à afficher le « a » correspondant. Ainsi,

 δ(q0, b, a) = (q1, ε) 

Ainsi, ce processus consistant à faire éclater « b » sera répété à moins que tous les symboles ne soient lus. Notez que l'action d'éclatement se produit uniquement dans l'état q1.

 δ(q1, b, a) = (q1, ε) 

Après avoir lu tous les b, tous les a correspondants devraient apparaître. Par conséquent, lorsque nous lisons ε comme symbole d’entrée, il ne devrait rien y avoir dans la pile. Le déplacement sera donc :

 δ(q1, ε, Z) = (q2, ε) 

Où

tableau.sort en java

PDA = ({q0, q1, q2}, {a, b}, {a, Z}, δ, q0, Z, {q2})

Nous pouvons résumer l’ID comme suit :

 δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa) δ(q0, b, a) = (q1, ε) δ(q1, b, a) = (q1, ε) δ(q1, ε, Z) = (q2, ε) 

Nous allons maintenant simuler ce PDA pour la chaîne d'entrée 'aaabbbbbb'.

 δ(q0, aaabbbbbb, Z) ⊢ δ(q0, aabbbbbb, aaZ) ⊢ δ(q0, abbbbbb, aaaaZ) ⊢ δ(q0, bbbbbb, aaaaaaZ) ⊢ δ(q1, bbbbb, aaaaaZ) ⊢ δ(q1, bbbb, aaaaZ) ⊢ δ(q1, bbb, aaaZ) ⊢ δ(q1, bb, aaZ) ⊢ δ(q1, b, aZ) ⊢ δ(q1, ε, Z) ⊢ δ(q2, ε) ACCEPT 

Exemple 2 :

Concevoir un PDA pour accepter une langue 0ⁿ1^m0ⁿ.

Solution: Dans ce PDA, n nombre de 0 sont suivis d'un nombre quelconque de 1 suivis de n nombre de 0. La logique de conception d’un tel PDA sera donc la suivante :

Poussez tous les 0 sur la pile lorsque vous rencontrez les premiers 0. Alors si nous lisons 1, ne faisons rien. Ensuite, lisez 0, et à chaque lecture de 0, extrayez un 0 de la pile.

Par exemple:

Ce scénario peut être écrit sous la forme ID comme :

 δ(q0, 0, Z) = δ(q0, 0Z) δ(q0, 0, 0) = δ(q0, 00) δ(q0, 1, 0) = δ(q1, 0) δ(q0, 1, 0) = δ(q1, 0) δ(q1, 0, 0) = δ(q1, ε) δ(q0, ε, Z) = δ(q2, Z) (ACCEPT state) 

Nous allons maintenant simuler ce PDA pour la chaîne d'entrée '0011100'.

 δ(q0, 0011100, Z) ⊢ δ(q0, 011100, 0Z) ⊢ δ(q0, 11100, 00Z) ⊢ δ(q0, 1100, 00Z) ⊢ δ(q1, 100, 00Z) ⊢ δ(q1, 00, 00Z) ⊢ δ(q1, 0, 0Z) ⊢ δ(q1, ε, Z) ⊢ δ(q2, Z) ACCEPT