Pourcentage – En mathématiques, un pourcentage est un chiffre ou un rapport qui représente une fraction sur 100. C'est une méthode utilisée pour exprimer une relation sans dimension entre deux nombres, similaire aux ratios, fractions et décimales. Les pourcentages sont généralement indiqués par le symbole % après le nombre. Le mot Pourcentage a été inventé à partir du mot latin Pour cent ce qui signifie par centaines . C'est une relation sans dimension entre deux nombres. Il est souvent désigné par le signe % ou pour cent ou PCT .
Dans cet article, nous couvrirons pourcentage comprenant sa définition, des exemples, la formule de pourcentage, comment calculer le pourcentage, etc.
Des exemples de pourcentages sont :
- 10 % équivaut à 10/100, soit 1/10 du nombre
- 20% équivaut à 20/100, soit 1/5 du nombre
Dans cet article, vous découvrirez en détail les pourcentages, les formules de pourcentage, comment calculer les pourcentages et d'autres.
Table des matières
- Qu’est-ce que le pourcentage ?
- Exemples de pourcentage
- Formule de pourcentage
- Comment calculer le pourcentage d’un nombre ?
- Formule de différence en pourcentage
- Formule d'augmentation en pourcentage
- Formule de diminution en pourcentage
- Comment calculer le pourcentage ?
- Conversion d'un pourcentage en fraction
- Conversion d'une fraction en pourcentage
- Graphique de pourcentage
- Tableau de pourcentage
- Différence entre pourcentage et pourcentage
- Pourcentage en mathématiques
- Astuces de pourcentage
- Comment calculer le pourcentage de notes
- Calculateur de pourcentage
- Exemple résolu de pourcentage
- Questions pratiques sur le pourcentage
Qu’est-ce que le pourcentage ?
Un F Une réaction dont le dénominateur est 100 est appelée un Pourcentage. c'est-à-dire que dans toutes les fractions où le dénominateur est 100, nous pouvons supprimer le dénominateur et mettre le signe %.
Par exemple, la fraction 23/100 peut s'écrire 23% . L’inverse est également vrai, c’est-à-dire que tout signe de pourcentage peut être facilement remplacé en convertissant le nombre en fraction avec le dénominateur 100. Par exemple, 45 % peut être converti en une fraction de 45/100.
- Les pourcentages sont également appelés nombres sans dimension , car ils n'ont aucune dimension. Ils sont le rapport de deux nombres de mêmes dimensions. Si nous disons 10 % d’un nombre, cela signifie 10 % de son tout.
- Les pourcentages peuvent également être représenté en valeurs décimales telles que 0,5 %, 0,75 %, etc.
Vérifier: Pourcentages – Questions et réponses sur les aptitudes
Exemples de pourcentage
Quelques exemples de fractions incluent ,
- Si Kabir obtient 95 points sur 100 à l'examen de mathématiques, cela change en fraction comme suit : 95/100 = 95 %
- Si le candidat A obtient 2 450 voix sur 10 000, il est représenté en pourcentage comme suit : 2 450/1 000 = 24,5/100 = 24,5 %.
De la même manière,
- 10/100 en pourcentage = 10%
- 50/100 en pourcentage = 50%
- 100/100 en pourcentage = 100%
L'image ci-dessous nous montre quelques exemples où le pourcentage est utilisé.

Formule de pourcentage
Formule de pourcentage est une formule utilisée pour trouver le montant ou la part d'une quantité en termes de cent. Ainsi, pour calculer le pourcentage, nous avons essentiellement besoin de trois variables. Premièrement, la valeur totale V 1 , la valeur actuelle V 2 , et la valeur en pourcentage P. L'équation algébrique pour cela sera :
Pourcentage (P%) = (Parties (V 2 ) / Entier (V 1 )) × 100

Comment calculer le pourcentage d’un nombre ?
Calculer le pourcentage d’un nombre est très simple, il vous suffit d’utiliser la formule mentionnée ci-dessous :
Pourcentage d'un nombre = Pourcentage/100 × Nombre
Exemple:
Calculez 5 % de 50
5 % de 50 = 5/100 × 50
5 % de 50 = 0,05 × 50
5% de 50 = 2,50
Formule de différence en pourcentage
Différence en pourcentage ou variation en pourcentage La formule est calculée lorsque la différence entre deux valeurs est divisée par la moyenne des mêmes valeurs. On peut dire que la différence en pourcentage est utilisée pour calculer la variation de la valeur sur la période donnée. Mathématiquement, on peut s'écrire :
Vérifier: Concept de base du pourcentage
Différence en pourcentage = (Différence absolue / Moyenne) × 100
Exemple: La différence en pourcentage entre 50 et 100 sera :
= |50-100|/ {(50+100)/2} × 100
= 50/75 ×100
= 66,66%
Il est exprimé sous forme de rapport et est un nombre sans unité
Formule d'augmentation en pourcentage
Nous pouvons utiliser la formule de différence en pourcentage pour trouver la variation de la valeur lorsqu’elle augmente sur une période de temps. Le formule d'augmentation en pourcentage est donné ci-dessous,
Pourcentage d'augmentation = (Augmentation de la valeur – Valeur d'origine / Moyenne) × 100
Formule de diminution en pourcentage
Nous pouvons utiliser la formule de différence en pourcentage pour trouver la variation de la valeur lorsqu’elle diminue sur une période de temps. Le formule de diminution en pourcentage est donné ci-dessous,
Pourcentage de diminution = (Valeur d'origine – Valeur de diminution / Moyenne) × 100
Note:
- Si la valeur obtenue est négative lors du calcul de la formule d’augmentation en pourcentage, il s’agit en fait d’une diminution en pourcentage.
- Si la valeur obtenue est négative lors du calcul de la formule de diminution en pourcentage, il s’agit en fait d’une augmentation en pourcentage.
- Le changement en pourcentage est également utilisé pour trouver le pourcentage d'erreurs en mathématiques, physique et chimie.
Comment calculer le pourcentage ?
La question la plus importante est de savoir comment calculer le pourcentage. Ainsi, les pourcentages peuvent facilement être calculés lorsque les valeurs sont données sous forme de fractions avec un dénominateur de 100. Sinon, nous devons convertir la fraction donnée en une fraction avec un dénominateur de 100, puis le pourcentage est facilement calculé.
Vérifier: Comment calculer le pourcentage ?
Par exemple, si 65/100 doit être calculé en pourcentage, la réponse peut facilement être calculée en supprimant le dénominateur 100 et en appliquant le symbole %, soit 65 %.
Exemple : convertissez 0,76 en pourcentage.
Solution:
0,76 = 0,76/1
0,76 = 76/100
0,76 = 76%
Comment calculer le pourcentage lorsque le total est de 100 ?
Si la valeur totale dans n'importe quel scénario atteint 100, le calcul du pourcentage est très simple car le nombre (au numérateur de la valeur) représente lui-même le pourcentage et le symbole % est ajouté.
Exemple : Supposons que lors de l'élection d'un représentant de classe, si l'élève A a obtenu 69 voix et que l'élève B a obtenu 31 voix, calculez le pourcentage de voix obtenues par A.
Solution:
opérateur ternaire java
Total des votes = 69 + 31 = 100
A obtenu des votes = 69
Votes de A (en pourcentage) = 69/100 = 69%
Comment calculer un pourcentage lorsque le total n’est PAS 100 ?
Si la valeur totale dans un scénario ne totalise pas 100, le pourcentage est calculé en faisant le total de 100 dans la fraction, puis les valeurs du numérateur deviennent le pourcentage.
Exemple : Supposons que Kabir ait 6 boules bleues, 8 boules rouges et 6 boules jaunes, le pourcentage de boules rouges qu'il possède ?
Solution:
Total des boules = boules rouges + boules bleues + boules jaunes
= 8 + 6 + 6 = 20 balles
Boules rouges = 8 boules
Pourcentage de boules rouges = 8/20
= (8/20) × (5/5) = 40/100 = 40 %
Conversion d'un pourcentage en fraction
Dans certains cas, nous recevons le pourcentage et devons le convertir en fraction nombre. Pour convertir des pourcentages en fractions, certains calculs sont nécessaires. Nous pouvons utiliser la formule,
Vérifier: Problèmes sur le pourcentage
Fraction = Pourcentage/100
Après l'avoir obtenu, réduisez-le davantage. Par exemple,
- Fraction de 25% = 25/100 = 1/4
- Fraction de 50% = 50/100 = 1/2
- Fraction de 75% = 75/100 = 3/4
- Fraction de 90% = 90/100 = 9/10
Conversion d'une fraction en pourcentage
Pour convertir une fraction en pourcentage, supposons que la fraction soit représentée par a/b, où a fait partie du tout b. Multiplier le numérateur et le dénominateur par 100.
On sait que 1/100 = 1%
Donc, l'équation peut s'écrire sous la forme,
a/b × 100 %.
Ainsi, pour convertir une fraction en pourcentage, multipliez la fraction par 100.
Graphique de pourcentage
Voyons le graphique en pourcentage des fractions converties en pourcentages,
Graphique de pourcentage | |||
|---|---|---|---|
| Fraction | Pourcentage | Fraction | Pourcentage |
1/1 | 100% | 1/11 | 9,09% |
1/2 | cinquante% | 1/12 | 8,33% |
1/3 | 33,33% | 1/13 | 7,69% |
1/4 | 25% | 1/14 | 7,14% texte CSS en gras |
1/5 | vingt% | 1/15 | 6,66% |
1/6 | 16,66% | 1/16 | 6,25% |
1/7 | 14,28% | 1/17 | 5,88% |
1/8 | 12,5% | 1/18 | 5,55% |
1/9 | 11,11% | 1/19 | 5,26% nœud de liste en Java |
1/10 | dix% | 1/20 | 5% |
Tableau de pourcentage
L'image ajoutée ci-dessous montre le tableau de pourcentage,
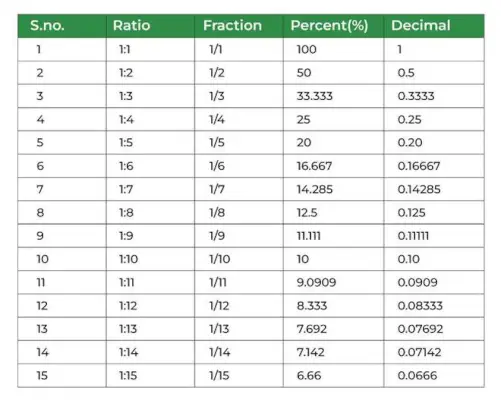
Différence entre pourcentage et pourcentage
Les mots le pourcentage et le pourcentage sont liés l'un à l'autre, mais il y a une différence entre les deux. Le pourcentage est toujours accompagné d'un nombre, par exemple 25 %.
Alors que le pourcentage n’a pas besoin d’un nombre pour être accompagné du terme.
Par exemple, le pourcentage de personnes ayant participé au vote en 2022 est supérieur au pourcentage de personnes ayant participé au vote en 2021.
Fractions, décimales, ratios et pourcentages sont également liés les uns aux autres.
Pourcentage en mathématiques
En mathématiques, le pourcentage s’écrit avec trois inconnues et variables possibles. Les trois termes sont connus :
- Pourcentage
- Partie
- Base
Par exemple, 50 % de 400 équivaut à 200. Ici, 50 est le pourcentage, 400 est la base et 200 est une partie.
Exemple : Si 25 % de 200 font 50, expliquez les différents termes du calcul.
25 % de 400 équivaut à 50. Ici, 25 est le pourcentage, 200 est la base et 50 est la partie.
En fraction, cela peut s’écrire :
Pièce/Base = 25/200 = 1/4
1/4 est la fraction obtenue. Cependant, nous avons appris à convertir des fractions en pourcentages. Par conséquent, multipliez 1/4 par 100,
1/4 × 100 = 25 %.
Astuces de pourcentage
Il existe des astuces de pourcentage qui peuvent être utilisées lors du calcul du pourcentage de nombres. L'astuce ci-dessous est la plus utilisée,
% x de y = % y de x
Exemple : Résolvez 300 % de 50.
Ici, résoudre 300 % de 50 peut être un peu long et délicat. Cependant, en utilisant cette astuce, cela peut être facilement résolu,
%x de y = %y de x
300 % de 50 = 50 % de 300
Désormais, résoudre 50 % de 300 est une solution relativement simple. 50 % de 300 ne représente que la moitié de 300. Par conséquent, 50 % de 300 correspond à 150.
Par conséquent, 300 % de 50 équivaut à 150.
Comment calculer le pourcentage de notes
Le pourcentage est principalement utilisé lors du calcul des notes des étudiants. Les notes des étudiants sont par rapport aux notes totales. Cette fraction est convertie en pourcentage en la multipliant par 100. De cette façon, nous pouvons calculer les notes en pourcentage. Voyons quelques exemples de notes obtenues en pourcentage,
| Notes obtenues | Total des notes | Notes en pourcentage (%) |
|---|---|---|
| cinquante | 100 | 50/100 × 100 = 50 % |
| 25 | cinquante | 25/50 × 100 = 50 % |
| 80 | 100 | 80/100 × 100 = 80 % |
| 33 | 100 | 33/100 × 100 = 33 % |
Calculateur de pourcentage
Le calculateur de pourcentage est un outil gratuit préparé sur techcodeview.com qui est utilisé pour trouver le pourcentage si deux nombres ou plus sont donnés. Consultez le calculateur de pourcentage ci-dessous :
Vérifier: Calculateur de pourcentage
En savoir plus,
- Fractions
- Formule de rapport et de proportions
- Formule de rendement en pourcentage
Exemple résolu de pourcentage
Voici quelques exemples de pourcentages :
Exemple 1 : Trouvez 15 % de 500.
Solution:
On peut trouver le pourcentage par formule,
DANS2= P × V1
DANS2= 15 % × 500
DANS2= (15 × 500) / 100
DANS2= 75.
Ainsi, 15 % de 500 équivaut à 75.
Vérifier: Questions en pourcentage
Exemple 2 : Trouvez 4 % de 1 300.
Solution:
On peut trouver le pourcentage par formule,
DANS2= P × V1
DANS2= 4 % × 1 300
DANS2= (4 × 1300) / 100
DANS2= 52.
Ainsi, 4% de 1300 équivaut à 52.
Exemple 3 : Quel pourcentage vaut 1 sur 3 000 ?
Solution:
On peut trouver le pourcentage par formule,
DANS2= P × V1
P = V2/ DANS1
P = 1/3000
Ainsi, P% = 1/3000 × 100
P% = (1/30)%
Ainsi, (1/30)% de 2000 est 500.
Exemple 4 : Si 10 % de x vaut 900. Trouvez x.
Solution:
Nous pouvons trouver le pourcentage par la formule,
DANS2= P × V1
DANS1= V2/P
DANS1= (V2× 100 ) /P%
DANS1= (900 × 100) / 10
DANS1= 9000
La valeur de x est donc 9 000.
Exemple 5 : Trouvez la valeur du pourcentage de blocs verts dans chaque cas.
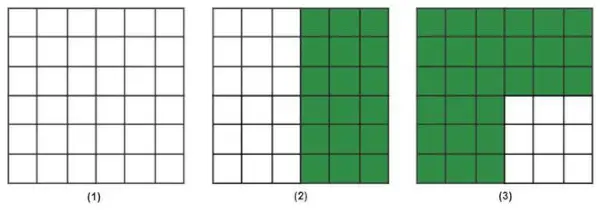
Solution:
Dans le premier cas, les blocs verts sont 0 et le total des blocs est 36.
Donc,
Pourcentage de blocs verts = 0/36 × 100 = 0 %.
Dans le deuxième cas, les blocs verts sont au nombre de 18 et le nombre total de blocs est de 36.
Donc,
Pourcentage de blocs verts = 18/36 × 100 = 50 %.
Dans le troisième cas, les blocs verts sont au nombre de 27 et le total des briques est au nombre de 36.
Donc,
Pourcentage de blocs verts = 27/36 × 100 = 75 %.
Exemple 6 : Quel pourcentage représente 15 sur 50 ?
Valeur d'origine = 15
Valeur totale = 50
La formule de pourcentage est,
Pourcentage = (Valeur originale/Valeur totale) × 100
= 15/50 × 100
= 30%
Exemple 7 : Quel pourcentage de 80 fait 20 ?
Valeur d'origine = 20
Valeur totale = 80
La formule de pourcentage est,
Pourcentage = (Valeur originale/Valeur totale) × 100
= 20/80 × 100
= 25%
Questions pratiques sur le pourcentage
Q1 : Un garçon a obtenu 450 marks sur 500 au total. Trouvez le pourcentage de notes.
Q2 : Trouvez le pourcentage de particules d'or pur dans l'or 18 carats étant donné que 24 carats est de l'or pur.
Q3 : Une bouteille d'acide de 5 litres a une concentration de 10 %. Trouvez la concentration d’acide pur dans la solution.
Q4 : Ram a obtenu 223 points sur 600 et a échoué à l'examen de 17 points. Trouvez le pourcentage de réussite des notes.
Conclusion – Pourcentage
Les pourcentages sont comme un langage universel pour les proportions. Au lieu de lutter avec des fractions ou des décimales, nous pouvons utiliser pourcentages pour exprimer n'importe quelle partie d'un tout sur 100 . Cela facilite la comparaison des choses, s'il s'agit de comprendre les remises sur une vente , visualiser les résultats d'une enquête ou suivre une recette. Des tâches quotidiennes à l'analyse de données complexes, les pourcentages sont un outil puissant pour donner un sens à notre monde, une partie à la fois.
FAQ sur le pourcentage
Qu'est-ce qu'un pourcentage de 100 % ?
Un pourcentage de 100 % équivaut en fait à 100
Comment définit-on le pourcentage ?
Un pourcentage est une façon d’exprimer une partie de quelque chose par rapport au tout, exprimé sous forme de fraction de 100.
Quel pourcentage de 1 an équivaut à 1 jour ?
Pour calculer le pourcentage de 1 an que représente 1 jour, on peut diviser le nombre de jours dans 1 jour par le nombre de jours dans 1 an puis multiplier par 100 % (pour l'exprimer en pourcentage).
Quel est le pourcentage MPC ?
La conversion de la MPC en pourcentage est aussi simple que de multiplier votre MPC par 9,5.
Qu’est-ce que le pourcentage ?
Le pourcentage est la représentation des nombres, la signification littérale du mot pourcentage est sur 100. En pourcentage, la valeur est représentée sur 100.
tableau en java
Quel est le symbole du pourcentage ?
Le symbole du pourcentage est %. Il est également connu en pourcentage.
Comment calculer le pourcentage ?
Pour calculer le pourcentage d'un nombre, il suffit de diviser le nombre obtenu par le nombre total et de multiplier la fraction par 100.
Qu’est-ce que le pourcentage de changement ?
La variation en pourcentage d'un nombre est la variation en pourcentage de l'ancienne valeur à la nouvelle valeur. Il est calculé à l'aide de la formule,
Changement en pourcentage = {(Différence entre l'ancienne valeur et la nouvelle valeur) / Ancienne valeur} × 100.
Quels sont des exemples de pourcentages ?
Le pourcentage est très souvent utilisé dans notre vie quotidienne, voici quelques exemples d'utilisation réelle du pourcentage.
- Le pourcentage des différents types de nutriments présents est indiqué au dos des emballages alimentaires.
- La batterie affiche sa puissance en pourcentage dans nos téléphones.
- Pourcentage de notes obtenues par les étudiants à l'examen.
Le pourcentage peut-il dépasser 100 ?
Oui, la valeur du pourcentage peut être supérieure à 100 si la valeur indiquée est supérieure à la valeur d'origine. Par exemple, 40/20 équivaut à 200 %.
