La loi du refroidissement de Newton est la loi fondamentale qui décrit le taux de transfert de chaleur d’un corps vers son environnement par rayonnement. Cette loi stipule que la vitesse à laquelle le corps rayonne de chaleur est directement proportionnelle à la différence de température du corps par rapport à son environnement, étant donné que la différence de température est faible. c'est-à-dire que plus la différence entre la température du corps et celle de son environnement est élevée, plus la chaleur est perdue et plus la température est basse, moins la chaleur est perdue. La loi du refroidissement de Newton est un cas particulier de la loi de Stefan-Boltzmann.

Dans cet article, nous découvrirons en détail la loi du refroidissement de Newton, la formule de la loi de refroidissement de Newton, sa dérivation, des exemples et d'autres.

Définition de la loi du refroidissement de Newton

Newton fut le premier à étudier la relation entre la chaleur perdue par un corps vers son environnement. Il affirme que plus la différence de température entre l'objet et son environnement est grande, plus le corps rayonne de chaleur.

La loi du refroidissement de Newton stipule que

Le taux de perte de chaleur d’un corps est directement proportionnel à la différence de température entre le corps et son environnement, étant donné que la différence de température n’est pas grande.

Cette loi est utilisée pour expliquer pourquoi l'eau chaude ou le lait laissé sur une table refroidit plus rapidement qu'un peu de lait ou d'eau tiède laissé sur la table. La loi du refroidissement de Newton nous aide à connaître la température de n’importe qui sans réellement la mesurer, compte tenu de la température initiale du corps et de la température de l’environnement.

Formule de la loi de refroidissement de Newton

La formule de la loi de refroidissement de Newton est une formule permettant de calculer la température d’un matériau lorsqu’il perd de la chaleur vers son environnement par rayonnement.

D’après la loi du refroidissement de Newton,

Le taux de perte de chaleur ( – dQ/dt) du corps est directement proportionnelle à la différence de température [ΔT = (T ₂ – T. ₁ )] du corps et de son environnement.

identifiants java valides

Nous pouvons le représenter comme,

– dQ/dt ∝ (T ₂ – T. ₁ )

– dQ/dt = k(T ₂ – T. ₁ )

où,
k est une constante de proportionnalité

En résolvant l'équation différentielle ci-dessus, nous obtenons,

T(t) = T _s + (T _Ô – T. _s ) C'est ^-kt

où,
t est le temps
T(t) est la température du corps au temps t
T _s est la température ambiante
T _Ô est la température initiale du corps
k est la constante de proportionnalité

Dérivation de la loi du refroidissement de Newton

La formule de la loi de refroidissement de Newton peut être dérivée en utilisant la solution de l’équation différentielle. Soit un corps de masse m, de capacité thermique spécifique s, à la température T₂et T₁est la température de l'environnement.

Si la température baisse légèrement dT ₂ à l'heure dt , alors la quantité de chaleur perdue est,

dQ = msdT ₂

Le taux de perte de chaleur est donné par,

dQ/dt = ms (dT ₂ /dt)

D’après la loi du refroidissement de Newton,

– dQ/dt = k(T ₂ – T. ₁ )

En comparant l'équation ci-dessus

– ms (dT ₂ /dt) = k (T ₂ – T. ₁ )

dT ₂ /(T ₂ –T ₁ ) = – (k/ms)dt

dT ₂ /(T ₂ – T. ₁ ) = – Kdt

où, K = k/m·s

Intégration de l'équation ci-dessus

enregistrer _C'est (T. ₂ – T. ₁ ) = – K t + c

T ₂ =T ₁ + C' et ^–Kt

où, C' = e ^c

La relation entre la baisse de température du corps et le temps est représentée à l'aide du graphique de refroidissement. La pente de ce graphique montre le taux de chute de la température.

PowerShell contre bash

La courbe de refroidissement est un graphique qui montre la relation entre la température corporelle et le temps. Le taux de chute de température est déterminé par la pente de la tangente à la courbe en tout point. L'image ajoutée ci-dessous montre la relation entre la chute de température et le temps.

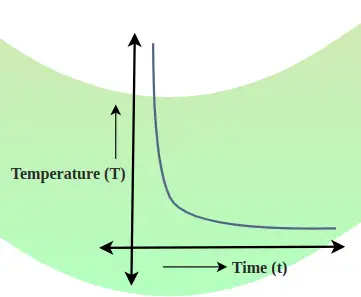
En général,

T(t) = T _UN +(T _H -T _UN )C'est ^-kt

où
T(t) est la température au temps t
T _UN est la température ambiante ou la température de l'environnement
T _H est la température de l'objet chaud
k est la constante positive et t est le temps

Méthodes pour appliquer la loi du refroidissement de Newton

À vitesse de refroidissement constante, la vitesse de refroidissement est liée à la température moyenne du corps pendant l'intervalle, nous pouvons alors calculer la valeur approximative, en utilisant la loi de refroidissement de Newton.

dθ/dt = k(q – q _s )

où,
q est la température du corps
q _s est la température de l'environnement

Maintenant, si la température moyenne du corps est q, où,

q = (q _je +q _F )/2

Vérification de la loi de refroidissement de Newton

Nous pouvons facilement vérifier la loi du refroidissement de Newton par l’expérience décrite ci-dessous :

Dans l’expérience, nous prenons un récipient à double paroi (V) avec de l’eau entre les deux parois. A l'intérieur du récipient à double paroi, on prend un calorimètre en cuivre (C) contenant de l'eau chaude.

Nous utilisons deux thermomètres T₂pour mesurer les températures de l'eau dans le calorimètre et T₁mesurer la température de l'eau chaude entre les doubles parois. Après des intervalles de temps égaux, les deux températures sont notées et un graphique entre le journal_C'est(T.₂–T₁) et le temps (t) est tracé sous la forme d'une ligne droite avec une pente négative.

Graphique de la loi du refroidissement de Newton

Le graphique de la loi de refroidissement de Newton est ajouté ci-dessous, dans ce graphique le journal de la différence entre les deux températures et le temps est affiché.

Limites de la loi du refroidissement de Newton

Diverses limites de la loi du refroidissement de Newton sont :

• La loi du refroidissement de Newton s’applique si la différence de température entre le corps et l’environnement est faible.
• La perte de chaleur par le corps se fait uniquement sous la forme de Radiation .
• La température ambiante doit rester constante pendant le refroidissement du corps, sinon la loi du refroidissement de Newton ne s’applique pas.

Applications de la loi du refroidissement de Newton

Diverses applications de la loi du refroidissement de Newton sont,

• Pour estimer combien de temps il faudra à un objet chaud pour refroidir jusqu'à une température spécifique.
• Déterminer la température d’une boisson dans un réfrigérateur après un certain temps.
• Il est utile d'indiquer l'heure du décès en examinant la température corporelle possible au moment du décès et la température corporelle actuelle.

En savoir plus,

rotation de l'arbre avl

• La capacité thermique spécifique
• Concept de base de la thermodynamique
• Processus thermodynamiques

Exemples résolus La loi du refroidissement de Newton

Exemple 1 : Une casserole remplie d'aliments chauds refroidit de 94 °C à 86 °C en 2 minutes lorsque la température ambiante est de 20 °C. Combien de temps faudra-t-il pour passer de 71 °C à 69 °C ?

Solution:

La moyenne de 94 °C et 86 °C est de 90 °C,

• T₂= 90 °C
• T₁= 20 °C

Déposez-les. de nourriture est de 8 °C en 2 minutes.

D’après la loi du refroidissement de Newton,

– dQ/dt = k(T ₂ –T ₁ )

8 °C /2 min = k(90 – 20)

4 = k(70) ………(1)

La moyenne de 69 °C et 71 °C est de 70 °C

• T₂= 70 °C
• T₁= 20 °C

D’après la loi du refroidissement de Newton,

2 °C /dt = k(70 – 20) ……(2)

D'après les équations (1) et (2),

Changement de temps = 0,7 min = =42 sec

Ainsi, les aliments mettront 42 secondes pour refroidir de 71 °C à 69 °C.

Exemple 2 : Un corps à une température de 40ºC est maintenu dans un environnement à température constante de 20ºC. On observe que sa température descend à 35ºC en 10 minutes. Trouvez combien de temps il faudra encore au corps pour atteindre une température de 30 ºC.

Solution:

Donné,

• q_je= (40 – 20)ºC
• q_F= (35 – 20)ºC

Selon la loi du refroidissement de Newton

q _F =q _je C'est ^-kt

Maintenant, pour l’intervalle pendant lequel la température passe de 40 ºC à 35 ºC.

(35 – 20) = (40 – 20) et^-(10k)

C'est^-10k= 3/4

-10k = (ln 4/3)

k = 0,2876/10

k = 0,02876

Maintenant, en utilisant à nouveau la formule de Newon,

(30 – 20) = (35 – 20)e^-kt

10 = 15e^-kt

C'est^-kt= 23

-kt = ln(2/3)

t = 0,40546/k

En utilisant la valeur du k,

t = 0,40546/0,02876

t = 14,098 minutes

Ainsi, le temps mis par le corps pour atteindre la température de 30ºC est de 14,098 minutes.

Exemple 3 : L'huile est chauffée à 70 ºC. Il refroidit à 50 ºC après 6 minutes. Calculer le temps mis par l'huile pour refroidir de 50 ºC à 40 ºC étant donné la température ambiante T _s = 25 ºC

Solution:

Donné,

Température de l'huile après 6 min, c'est-à-dire que T(t) est égal à 50 ºC

communication analogique

• Température ambiante T_s= 25 ºC
• Température de l'huile, T_Ô= 70 ºC
• Temps de refroidissement à 50ºC = 6 min

D’après la loi du refroidissement de Newton,

T(t) = T_s+ (T₀– T._s) C'est^-kt

{T(t) – T_s}/(T_Ô– T._s) = et^-kt

-kt = ln[(T(t) – T_s)/(T_Ô– T._s)] ………(1)

Remplacer les valeurs

-kt = ln[(50 – 25)/(70 – 25)]

-k = (ln 0,55556)/6

k = 0,09796

La température moyenne de 50 ºC à 40 ºC est égale à 45 ºC

Encore une fois en utilisant la loi de refroidissement de Newton

-(0,09796)t = ln[(45 – 25)/(70 – 25)]

-0,09796t = ln(0,44444)

0,09796t = 0,81093

t = 0,09796/0,58778 = 8,278 minutes

Ainsi, le temps nécessaire à l'huile pour refroidir de 50 ºC à 40 ºC est 8,278 minutes

Exemple 4 : L'eau est chauffée à 80 ºC pendant 10 min. Quelle serait sa température en degrés Celsius, si k = 0,056 par minute et que la température ambiante est de 25 ºC ?

Solution:

Donné,

• Température ambiante T_s= 25 ºC
• Température de l'eau T₀= 80 ºC
• Temps pendant lequel l'eau est chauffée (t) = 10 min
• Valeur de la constante k = 0,056.

D’après la loi du refroidissement de Newton,

T(t) = T_s+ (T₀– T._s) C'est^-kt

Remplacement de la valeur

T(t)= 25 + (80 – 25)e^-(0,056×10)

T(t) = 25 + 55e^-(0,056×10)

T(t) = 25 + 31,42

T(t) = 56,42

Après 10 minutes, la température de l'eau serait 56,42 ºC.

FAQ sur la loi du refroidissement de Newton

Q1 : Qu’est-ce que la loi du refroidissement de Newton ?

Répondre:

La loi du refroidissement de Newton stipule que le taux de perte de chaleur par un corps est directement proportionnel à la différence de température entre le corps et son environnement.

Q2 : Qu'est-ce que la formule de la loi de refroidissement de Newton ?

Répondre:

La formule de la loi de refroidissement de Newton stipule que :

T(t) = T _s + (T _Ô – T. _s ) C'est ^-kt

structures de données en Java

Q3 : Qu’est-ce que k dans la loi du refroidissement de Newton ?

Répondre:

Le k dans la formule de la loi du refroidissement de Newton, c'est la constante qui dépend du matériau, c'est-à-dire que changer le matériau change la k dans la loi du refroidissement de Newton.

Q4 : Pourquoi le lait chaud est-il plus facile à boire dans un bol que dans un verre ?

Répondre:

Le bol a une plus grande surface que le verre, donc plus de chaleur se perd dans son environnement sous forme de rayonnement thermique à travers le bol et il nous est donc plus facile de boire du lait chaud dans le bol.