Étant donné un tableau 3D arr[l][m][n], la tâche consiste à trouver la somme minimale du chemin depuis la première cellule du tableau jusqu'à la dernière cellule du tableau. Nous ne pouvons traverser que vers un élément adjacent, c'est-à-dire qu'à partir d'une cellule donnée (i j k), les cellules (i+1 j k) (i j+1 k) et (i j k+1) peuvent être parcourues. Le parcours en diagonale n'est pas autorisé. Nous pouvons supposer que tous les coûts sont des entiers positifs.
Exemples :
Input : arr[][][]= { {{1 2} {3 4}} {{4 8} {5 2}} }; Output : 9 Explanation : arr[0][0][0] + arr[0][0][1] + arr[0][1][1] + arr[1][1][1] Input : { { {1 2} {4 3}} { {3 4} {2 1}} }; Output : 7 Explanation : arr[0][0][0] + arr[0][0][1] + arr[0][1][1] + arr[1][1][1] Considérons un tableau 3D arr[2][2][2] représenté par un cuboïde ayant les valeurs suivantes :
arr[][][] = {{{1 2} {3 4}} { {4 8} {5 2}}}; Result = 9 is calculated as: 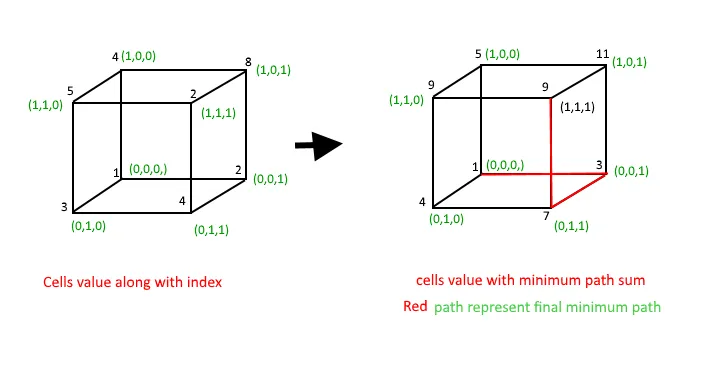
Ce problème est similaire à Chemin de coût minimum. et peut être résolu à l'aide de la programmation dynamique.
// Array for storing result int tSum[l][m][n]; tSum[0][0][0] = arr[0][0][0]; /* Initialize first row of tSum array */ for (i = 1; i < l; i++) tSum[i][0][0] = tSum[i-1][0][0] + arr[i][0][0]; /* Initialize first column of tSum array */ for (j = 1; j < m; j++) tSum[0][j][0] = tSum[0][j-1][0] + arr[0][j][0]; /* Initialize first width of tSum array */ for (k = 1; k < n; k++) tSum[0][0][k] = tSum[0][0][k-1] + arr[0][0][k]; /* Initialize first row- First column of tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) tSum[i][j][0] = min(tSum[i-1][j][0] tSum[i][j-1][0] INT_MAX) + arr[i][j][0]; /* Initialize first row- First width of tSum array */ for (i = 1; i < l; i++) for (k = 1; k < n; k++) tSum[i][0][k] = min(tSum[i-1][0][k] tSum[i][0][k-1] INT_MAX) + arr[i][0][k]; /* Initialize first width- First column of tSum array */ for (k = 1; k < n; k++) for (j = 1; j < m; j++) tSum[0][j][k] = min(tSum[0][j][k-1] tSum[0][j-1][k] INT_MAX) + arr[0][j][k]; /* Construct rest of the tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) for (k = 1; k < n; k++) tSum[i][j][k] = min(tSum[i-1][j][k] tSum[i][j-1][k] tSum[i][j][k-1]) + arr[i][j][k]; return tSum[l-1][m-1][n-1];C++
// C++ program for Min path sum of 3D-array #include
// Java program for Min path sum of 3D-array import java.io.*; class GFG { static int l =3; static int m =3; static int n =3; // A utility function that returns minimum // of 3 integers static int min(int x int y int z) { return (x < y)? ((x < z)? x : z) : ((y < z)? y : z); } // function to calculate MIN path sum of 3D array static int minPathSum(int arr[][][]) { int i j k; int tSum[][][] =new int[l][m][n]; tSum[0][0][0] = arr[0][0][0]; /* Initialize first row of tSum array */ for (i = 1; i < l; i++) tSum[i][0][0] = tSum[i-1][0][0] + arr[i][0][0]; /* Initialize first column of tSum array */ for (j = 1; j < m; j++) tSum[0][j][0] = tSum[0][j-1][0] + arr[0][j][0]; /* Initialize first width of tSum array */ for (k = 1; k < n; k++) tSum[0][0][k] = tSum[0][0][k-1] + arr[0][0][k]; /* Initialize first row- First column of tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) tSum[i][j][0] = min(tSum[i-1][j][0] tSum[i][j-1][0] Integer.MAX_VALUE) + arr[i][j][0]; /* Initialize first row- First width of tSum array */ for (i = 1; i < l; i++) for (k = 1; k < n; k++) tSum[i][0][k] = min(tSum[i-1][0][k] tSum[i][0][k-1] Integer.MAX_VALUE) + arr[i][0][k]; /* Initialize first width- First column of tSum array */ for (k = 1; k < n; k++) for (j = 1; j < m; j++) tSum[0][j][k] = min(tSum[0][j][k-1] tSum[0][j-1][k] Integer.MAX_VALUE) + arr[0][j][k]; /* Construct rest of the tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) for (k = 1; k < n; k++) tSum[i][j][k] = min(tSum[i-1][j][k] tSum[i][j-1][k] tSum[i][j][k-1]) + arr[i][j][k]; return tSum[l-1][m-1][n-1]; } // Driver program public static void main (String[] args) { int arr[][][] = { { {1 2 4} {3 4 5} {5 2 1}} { {4 8 3} {5 2 1} {3 4 2}} { {2 4 1} {3 1 4} {6 3 8}} }; System.out.println ( minPathSum(arr)); } } // This code is contributed by vt_m
# Python3 program for Min # path sum of 3D-array l = 3 m = 3 n = 3 # A utility function # that returns minimum # of 3 integers def Min(x y z): return min(min(xy)z) # function to calculate MIN # path sum of 3D array def minPathSum(arr): tSum = [[[0 for k in range(n)]for j in range(m)] for i in range(l)] tSum[0][0][0] = arr[0][0][0] # Initialize first # row of tSum array for i in range(1l): tSum[i][0][0] = tSum[i - 1][0][0] + arr[i][0][0] # Initialize first column # of tSum array for j in range(1m): tSum[0][j][0] = tSum[0][j - 1][0] + arr[0][j][0] # Initialize first # width of tSum array for k in range(1n): tSum[0][0][k] = tSum[0][0][k - 1] + arr[0][0][k] # Initialize first # row- First column of # tSum array for i in range(1l): for j in range(1m): tSum[i][j][0] = Min(tSum[i - 1][j][0]tSum[i][j - 1][0]1000000000) + arr[i][j][0]; # Initialize first # row- First width of # tSum array for i in range(1l): for k in range(1n): tSum[i][0][k] = Min(tSum[i - 1][0][k]tSum[i][0][k - 1]1000000000) + arr[i][0][k] # Initialize first # width- First column of # tSum array for k in range(1n): for j in range(1m): tSum[0][j][k] = Min(tSum[0][j][k - 1]tSum[0][j - 1][k]1000000000) + arr[0][j][k] # Construct rest of # the tSum array for i in range(1l): for j in range(1m): for k in range(1n): tSum[i][j][k] = Min(tSum[i - 1][j][k]tSum[i][j - 1][k]tSum[i][j][k - 1]) + arr[i][j][k] return tSum[l-1][m-1][n-1] # Driver Code arr = [[[1 2 4] [3 4 5] [5 2 1]] [[4 8 3] [5 2 1] [3 4 2]] [[2 4 1] [3 1 4] [6 3 8]]] print(minPathSum(arr)) # This code is contributed by shinjanpatra
// C# program for Min // path sum of 3D-array using System; class GFG { static int l = 3; static int m = 3; static int n = 3; // A utility function // that returns minimum // of 3 integers static int min(int x int y int z) { return (x < y) ? ((x < z) ? x : z) : ((y < z) ? y : z); } // function to calculate MIN // path sum of 3D array static int minPathSum(int []arr) { int i j k; int [ ]tSum = new int[l m n]; tSum[0 0 0] = arr[0 0 0]; /* Initialize first row of tSum array */ for (i = 1; i < l; i++) tSum[i 0 0] = tSum[i - 1 0 0] + arr[i 0 0]; /* Initialize first column of tSum array */ for (j = 1; j < m; j++) tSum[0 j 0] = tSum[0 j - 1 0] + arr[0 j 0]; /* Initialize first width of tSum array */ for (k = 1; k < n; k++) tSum[0 0 k] = tSum[0 0 k - 1] + arr[0 0 k]; /* Initialize first row- First column of tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) tSum[i j 0] = min(tSum[i - 1 j 0] tSum[i j - 1 0] int.MaxValue) + arr[i j 0]; /* Initialize first row- First width of tSum array */ for (i = 1; i < l; i++) for (k = 1; k < n; k++) tSum[i 0 k] = min(tSum[i - 1 0 k] tSum[i 0 k - 1] int.MaxValue) + arr[i 0 k]; /* Initialize first width- First column of tSum array */ for (k = 1; k < n; k++) for (j = 1; j < m; j++) tSum[0 j k] = min(tSum[0 j k - 1] tSum[0 j - 1 k] int.MaxValue) + arr[0 j k]; /* Construct rest of the tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) for (k = 1; k < n; k++) tSum[i j k] = min(tSum[i - 1 j k] tSum[i j - 1 k] tSum[i j k - 1]) + arr[i j k]; return tSum[l-1m-1n-1]; } // Driver Code static public void Main () { int [ ]arr= {{{1 2 4} {3 4 5} {5 2 1}} {{4 8 3} {5 2 1} {3 4 2}} {{2 4 1} {3 1 4} {6 3 8}}}; Console.WriteLine(minPathSum(arr)); } } // This code is contributed by ajit
<script> // Javascript program for Min // path sum of 3D-array var l = 3; var m = 3; var n = 3; // A utility function // that returns minimum // of 3 integers function min(x y z) { return (x < y) ? ((x < z) ? x : z) : ((y < z) ? y : z); } // function to calculate MIN // path sum of 3D array function minPathSum(arr) { var i j k; var tSum = Array(l); for(var i = 0; i<l;i++) { tSum[i] = Array.from(Array(m) ()=>Array(n)); } tSum[0][0][0] = arr[0][0][0]; /* Initialize first row of tSum array */ for (i = 1; i < l; i++) tSum[i][0][0] = tSum[i - 1][0][0] + arr[i][0][0]; /* Initialize first column of tSum array */ for (j = 1; j < m; j++) tSum[0][j][0] = tSum[0][j - 1][0] + arr[0][j][0]; /* Initialize first width of tSum array */ for (k = 1; k < n; k++) tSum[0][0][k] = tSum[0][0][k - 1] + arr[0][0][k]; /* Initialize first row- First column of tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) tSum[i][j][0] = min(tSum[i - 1][j][0] tSum[i][j - 1][0] 1000000000) + arr[i][j][0]; /* Initialize first row- First width of tSum array */ for (i = 1; i < l; i++) for (k = 1; k < n; k++) tSum[i][0][k] = min(tSum[i - 1][0][k] tSum[i][0][k - 1] 1000000000) + arr[i][0][k]; /* Initialize first width- First column of tSum array */ for (k = 1; k < n; k++) for (j = 1; j < m; j++) tSum[0][j][k] = min(tSum[0][j][k - 1] tSum[0][j - 1][k] 1000000000) + arr[0][j][k]; /* Construct rest of the tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) for (k = 1; k < n; k++) tSum[i][j][k] = min(tSum[i - 1][j][k] tSum[i][j - 1][k] tSum[i][j][k - 1]) + arr[i][j][k]; return tSum[l-1][m-1][n-1]; } // Driver Code var arr= [[[1 2 4] [3 4 5] [5 2 1]] [[4 8 3] [5 2 1] [3 4 2]] [[2 4 1] [3 1 4] [6 3 8]]]; document.write(minPathSum(arr)); </script>
Sortir:
20
Complexité temporelle : O(l*m*n)
Espace Auxiliaire : O(l*m*n)
