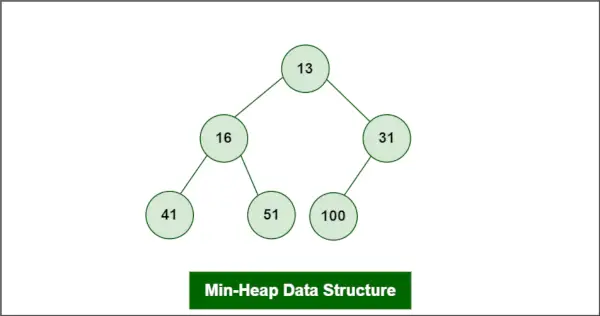
UN Min-Tas est défini comme un type de La structure de données en tas est un type d'arbre binaire couramment utilisé en informatique à diverses fins, notamment le tri, la recherche et l'organisation des données.
Introduction à Min-Heap – Tutoriels sur la structure des données et les algorithmes
Objectif et cas d'utilisation de Min-Heap :
- Implémentation de la file d'attente prioritaire : L'une des principales utilisations de la structure de données de tas consiste à implémenter des files d'attente prioritaires.
- L'algorithme de Dijkstra : L'algorithme de Dijkstra est un algorithme de chemin le plus court qui trouve le chemin le plus court entre deux nœuds dans un graphe. Un tas min peut être utilisé pour garder une trace des nœuds non visités avec la plus petite distance du nœud source.
- Tri: Un tas min peut être utilisé comme algorithme de tri pour trier efficacement une collection d'éléments par ordre croissant.
- Résultat médian : Un tas min peut être utilisé pour trouver efficacement la médiane d'un flux de nombres. Nous pouvons utiliser un tas min pour stocker la plus grande moitié des nombres et un tas max pour stocker la plus petite moitié. La médiane sera la racine du tas min.
Structure de données Min-Heap dans différentes langues :
1. Min-Heap en C++
Un tas min peut être implémenté en utilisant le File d'attente de priorité conteneur de la bibliothèque de modèles standard (STL). Le File d'attente de priorité Le conteneur est un type d'adaptateur de conteneur qui permet de stocker des éléments dans une structure de données de type file d'attente dans laquelle chaque élément est associé à une priorité.
Syntaxe :
C++ priority_queue < int, vector , plus grand > minH;>
2. Min-Heap en Java
En Java, un tas min peut être implémenté en utilisant le File d'attente de priorité classe de paquet java.util . La classe PriorityQueue est une file d'attente prioritaire qui permet de stocker des éléments dans une structure de données de type file d'attente dans laquelle chaque élément est associé à une priorité.
Syntaxe :
Java PriorityQueue minHeap = nouvelle PriorityQueue ();>
3. Min-Heap en Python
En Python, un tas min peut être implémenté en utilisant le tas module, qui fournit des fonctions pour implémenter des tas. Plus précisément, le tas Le module fournit un moyen de créer et de manipuler des structures de données de tas.
Syntaxe:
Python heap = [] heapify(heap)>
4. Min-Heap en C#
En C#, un tas min peut être implémenté à l'aide de la classe PriorityQueue du Espace de noms System.Collections.Generic . La classe PriorityQueue est une file d'attente prioritaire qui permet de stocker des éléments dans une structure de données de type file d'attente dans laquelle chaque élément est associé à une priorité.
Syntaxe:
C# var minHeap = new PriorityQueue ();>
5. Min-tas en JavaScript
Un tas min est un arbre binaire dans lequel chaque nœud a une valeur inférieure ou égale à celle de ses enfants. En JavaScript, vous pouvez implémenter un tas min à l'aide d'un tableau, où le premier élément représente le nœud racine et les enfants d'un nœud à l'index. je sont situés aux indices 2i+1 et 2i+2.
Syntaxe:
Javascript const minHeap = new MinHeap();>
Différence entre le tas minimum et le tas maximum :
|
| Tas minimum | Tas maximum |
|---|---|---|
| 1. | Dans un Min-Heap, la clé présente sur le nœud racine doit être inférieure ou égale à parmi les clés présentes sur tous ses enfants. | Dans un Max-Heap, la clé présente sur le nœud racine doit être supérieure ou égale à parmi les clés présentes sur tous ses enfants. |
| 2. | Dans un Min-Heap, l'élément clé minimum est présent à la racine. | Dans un Max-Heap, l'élément clé maximum est présent à la racine. |
| 3. | Un Min-Heap utilise la priorité croissante. | Un Max-Heap utilise la priorité décroissante. |
| 4. | Dans la construction d’un Min-Heap, le plus petit élément est prioritaire. | Dans la construction d’un Max-Heap, le plus gros élément est prioritaire. |
| 5. | Dans un Min-Heap, le plus petit élément est le premier à être extrait du tas. | Dans un Max-Heap, le plus grand élément est le premier à être extrait du tas. |
Implémentation interne de la structure de données Min-Heap :
UN Le tas minimum est généralement représenté sous forme de tableau .
- L'élément racine sera à Arr[0] .
- Pour tout ième nœud Arr[je] :
- Arr[(je -1) / 2] renvoie son nœud parent.
- Arr[(2 * i) + 1] renvoie son nœud enfant gauche.
- Arr[(2 * i) + 2] renvoie son nœud enfant droit.
L’implémentation interne du Min-Heap nécessite 3 étapes majeures :
- Insertion : Pour insérer un élément dans le tas min, nous ajoutons d'abord l'élément à la fin du tableau, puis ajustons la propriété du tas en échangeant à plusieurs reprises l'élément avec son parent jusqu'à ce qu'il soit dans la position correcte.
- Effacement : Pour supprimer l'élément minimum du tas min, nous échangeons d'abord le nœud racine avec le dernier élément du tableau, supprimons le dernier élément, puis ajustons la propriété du tas en échangeant à plusieurs reprises l'élément avec son plus petit enfant jusqu'à ce qu'il soit dans le tas min. position correcte.
- Heapifier : Une opération heapify peut être utilisée pour créer un tas min à partir d'un tableau non trié.
Opérations sur la structure de données Min-heap et leur mise en œuvre :
Voici quelques opérations courantes qui peuvent être effectuées sur une structure de données de tas,
1. Insertion dans la structure de données Min-Heap :
Les éléments peuvent être insérés dans le tas en suivant une approche similaire à celle décrite ci-dessus pour la suppression. L'idée est de :
maman kulkarni
- L'opération d'insertion dans un min-heap implique les étapes suivantes :
- Ajoutez le nouvel élément à la fin du tas, à la prochaine position disponible dans le dernier niveau de l'arborescence.
- Comparez le nouvel élément avec son parent. Si le parent est supérieur au nouvel élément, échangez-les.
- Répétez l'étape 2 jusqu'à ce que le parent soit inférieur ou égal au nouvel élément, ou jusqu'à ce que le nouvel élément atteigne la racine de l'arborescence.
- Le nouvel élément est maintenant dans sa position correcte dans le tas min et la propriété heap est satisfaite.
Illustration:
Supposons que le tas soit un min-heap comme :
Insertion dans le tas min
Implémentation de l'opération d'insertion dans Min-Heap :
C++ #include #include using namespace std; // Function to insert a new element into the min-heap void insert_min_heap(vector & heap, int value) { // Ajoute le nouvel élément à la fin du tas heap.push_back(value); // Récupère l'index du dernier élément int index = heap.size() - 1; // Comparez le nouvel élément avec son parent et échangez si // nécessaire while (index> 0 && heap[(index - 1) / 2]> heap[index]) { swap(heap[index], heap[(index - 1) / 2]); // Remonte l'arborescence jusqu'au parent de l'élément // actuel index = (index - 1) / 2; } } // Fonction principale pour tester la fonction insert_min_heap int main() { vector tas; valeurs int[] = { 10, 7, 11, 5, 4, 13 } ; int n = taille de (valeurs) / taille de (valeurs [0]); pour (int je = 0; je< n; i++) { insert_min_heap(heap, values[i]); cout << 'Inserted ' << values[i] << ' into the min-heap: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; } return 0; }>
Java import java.util.*; public class GFG { // Function to insert a new element into the min-heap public static void insertMinHeap(int[] heap, int size, int value) { // Add the new element to the end of the heap heap[size] = value; // Get the index of the last element int index = size; // Compare the new element with its parent and swap // if necessary while (index>0 && tas[(index - 1) / 2]> tas[index]) { swap(tas, index, (index - 1) / 2); // Remonte l'arborescence jusqu'au parent de l'élément // actuel index = (index - 1) / 2; } } // Fonction pour échanger deux éléments dans un tableau public static void swap(int[] arr, int i, int j) { int temp = arr[i]; arr[je] = arr[j]; arr[j] = temp; } // Fonction principale pour tester la fonction insertMinHeap public static void main(String[] args) { int[] heap = new int[6]; valeurs int[] = { 10, 7, 11, 5, 4, 13 } ; taille entière = 0 ; pour (int je = 0; je< values.length; i++) { insertMinHeap(heap, size, values[i]); size++; System.out.print('Inserted ' + values[i] + ' into the min-heap: '); for (int j = 0; j < size; j++) { System.out.print(heap[j] + ' '); } System.out.println(); } } }> Python3 def insert_min_heap(heap, value): # Add the new element to the end of the heap heap.append(value) # Get the index of the last element index = len(heap) - 1 # Compare the new element with its parent and swap if necessary while index>0 et tas[(index - 1) // 2]> tas[index] : tas[index], tas[(index - 1) // 2] = tas[(index - 1) // 2], tas[ index] # Remonter l'arborescence jusqu'au parent de l'élément actuel index = (index - 1) // 2 tas = [] valeurs = [10, 7, 11, 5, 4, 13] pour la valeur dans les valeurs : insert_min_heap( tas, valeur) print(f'Inséré {valeur} dans le tas min : {heap}')> C# using System; using System.Collections.Generic; public class Program { // Function to insert a new element into the min-heap static void InsertMinHeap(List heap, int value) { // Ajoute le nouvel élément à la fin du tas heap.Add(value); // Récupère l'index du dernier élément int index = heap.Count - 1; // Comparez le nouvel élément avec son parent et échangez // si nécessaire while (index> 0 && heap[(index - 1) / 2]> heap[index]) { int temp = heap[index]; tas[index] = tas[(index - 1) / 2]; tas[(index - 1) / 2] = temp; // Remonte l'arborescence jusqu'au parent de l'élément // actuel index = (index - 1) / 2; } } // Fonction principale pour tester la fonction InsertMinHeap public static void Main() { List tas = nouvelle liste (); valeurs int[] = { 10, 7, 11, 5, 4, 13 } ; foreach (int valeur en valeurs) { InsertMinHeap (tas, valeur); Console.Write('Inséré ' + valeur + ' dans le tas min : '); foreach (int élément dans le tas) { Console.Write (element + ' '); } Console.WriteLine(); } } }> Javascript function insertMinHeap(heap, value) { heap.push(value); let index = heap.length - 1; let parentIndex = Math.floor((index - 1) / 2); while (index>0 && tas[parentIndex]> tas[index]) { [tas[index], tas[parentIndex]] = [tas[parentIndex], tas[index]]; index = parentIndex ; parentIndex = Math.floor((index - 1) / 2); } } // Exemple d'utilisation const heap = []; valeurs const = [10, 7, 11, 5, 4, 13] ; for (valeur const des valeurs) { insertMinHeap(heap, value); console.log(`Inséré ${value} dans le min-heap : ${heap}`); }> Sortir
Inserted 10 into the min-heap: 10 Inserted 7 into the min-heap: 7 10 Inserted 11 into the min-heap: 7 10 11 Inserted 5 into the min-heap: 5 7 11 10 Inserted 4 into the min-heap: 4 5 11 10 7 Inser...>
Complexité temporelle : O(log(n)) ( où n est le nombre d'éléments dans le tas )
Espace auxiliaire : Sur)
2. Suppression dans la structure de données Min-Heap :
Suppression du plus petit élément (la racine) du tas min. La racine est remplacée par le dernier élément du tas, puis la propriété du tas est restaurée en échangeant la nouvelle racine avec son plus petit enfant jusqu'à ce que le parent soit plus petit que les deux enfants ou jusqu'à ce que la nouvelle racine atteigne un nœud feuille.
- Remplacez la racine ou l'élément à supprimer par le dernier élément.
- Supprimez le dernier élément du tas.
- Puisque le dernier élément est désormais placé à la position du nœud racine. Il se peut donc qu’il ne suive pas la propriété du tas. Par conséquent, empilez le dernier nœud placé à la position de la racine.
Illustration :
Supposons que le Heap soit un Min-Heap tel que :
Structure de données Min-Heap
L'élément à supprimer est root, soit 13.
Processus :
Le dernier élément est 100.
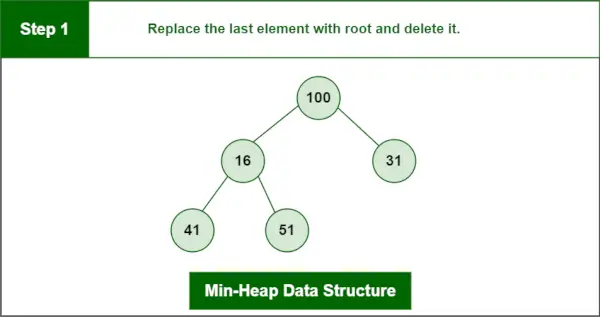
Étape 1: Remplacez le dernier élément par root et supprimez-le.
Structure de données Min-Heap
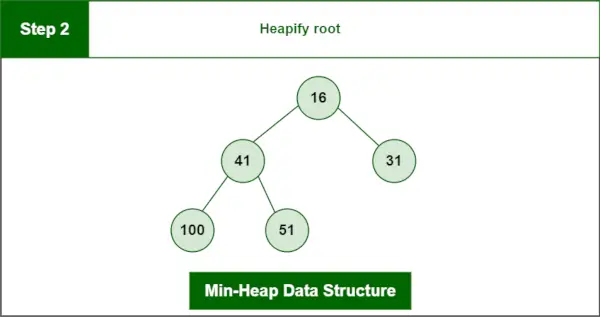
Étape 2 : Accumulez la racine.
Tas final :
Structure de données Min-Heap
Implémentation de l'opération de suppression dans Min-Heap :
C++ #include #include using namespace std; // Function to insert a new element into the min-heap void insert_min_heap(vector & heap, int value) { // Ajoute le nouvel élément à la fin du tas heap.push_back(value); // Récupère l'index du dernier élément int index = heap.size() - 1; // Comparez le nouvel élément avec son parent et échangez si // nécessaire while (index> 0 && heap[(index - 1) / 2]> heap[index]) { swap(heap[index], heap[(index - 1) / 2]); // Remonte l'arborescence jusqu'au parent de l'élément // actuel index = (index - 1) / 2; } } // Fonction pour supprimer un nœud du min-heap void delete_min_heap(vector & tas, valeur int) { // Trouver l'index de l'élément à supprimer int index = -1; pour (int je = 0; je< heap.size(); i++) { if (heap[i] == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last // element heap[index] = heap[heap.size() - 1]; // Remove the last element heap.pop_back(); // Heapify the tree starting from the element at the // deleted index while (true) { int left_child = 2 * index + 1; int right_child = 2 * index + 2; int smallest = index; if (left_child < heap.size() && heap[left_child] < heap[smallest]) { smallest = left_child; } if (right_child < heap.size() && heap[right_child] < heap[smallest]) { smallest = right_child; } if (smallest != index) { swap(heap[index], heap[smallest]); index = smallest; } else { break; } } } // Main function to test the insert_min_heap and // delete_min_heap functions int main() { vector tas; valeurs int[] = { 13, 16, 31, 41, 51, 100 } ; int n = taille de (valeurs) / taille de (valeurs [0]); pour (int je = 0; je< n; i++) { insert_min_heap(heap, values[i]); } cout << 'Initial heap: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; delete_min_heap(heap, 13); cout << 'Heap after deleting 13: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; return 0; }>
Java import java.util.*; public class GFG { // Function to insert a new element into the min-heap public static void insertMinHeap(List heap, int value) { // Ajoute le nouvel élément à la fin du tas heap.add(value); // Récupère l'index du dernier élément int index = heap.size() - 1; // Comparez le nouvel élément avec son parent et échangez // si nécessaire while (index> 0 && heap.get((index - 1) / 2)> heap.get(index)) { Collections.swap(heap, index, (indice - 1) / 2); // Remonte l'arborescence jusqu'au parent de l'élément // actuel index = (index - 1) / 2; } } // Fonction pour supprimer un nœud du min-heap public static void deleteMinHeap(List tas, valeur int) { // Trouver l'index de l'élément à supprimer int index = -1; pour (int je = 0; je< heap.size(); i++) { if (heap.get(i) == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last // element heap.set(index, heap.get(heap.size() - 1)); // Remove the last element heap.remove(heap.size() - 1); // Heapify the tree starting from the element at the // deleted index while (true) { int leftChild = 2 * index + 1; int rightChild = 2 * index + 2; int smallest = index; if (leftChild < heap.size() && heap.get(leftChild) < heap.get(smallest)) { smallest = leftChild; } if (rightChild < heap.size() && heap.get(rightChild) < heap.get(smallest)) { smallest = rightChild; } if (smallest != index) { Collections.swap(heap, index, smallest); index = smallest; } else { break; } } } // Main function to test the insertMinHeap and // deleteMinHeap functions public static void main(String[] args) { List tas = nouvelle liste de tableaux (); valeurs int[] = { 13, 16, 31, 41, 51, 100 } ; int n = valeurs.longueur; pour (int je = 0; je< n; i++) { insertMinHeap(heap, values[i]); } System.out.print('Initial heap: '); for (int j = 0; j < heap.size(); j++) { System.out.print(heap.get(j) + ' '); } System.out.println(); deleteMinHeap(heap, 13); System.out.print('Heap after deleting 13: '); for (int j = 0; j < heap.size(); j++) { System.out.print(heap.get(j) + ' '); } System.out.println(); } }> Python3 def insert_min_heap(heap, value): heap.append(value) index = len(heap) - 1 while index>0 et tas[(index - 1) // 2]> tas[index] : tas[index], tas[(index - 1) // 2] = tas[(index - 1) // 2], tas[ index] index = (index - 1) // 2 def delete_min_heap(heap, value) : index = -1 pour i in range(len(heap)) : si tas[i] == valeur : index = je casse si index == -1 : return heap[index] = heap[-1] heap.pop() while True : left_child = 2 * index + 1 right_child = 2 * index + 2 smallest = index si left_child< len(heap) and heap[left_child] < heap[smallest]: smallest = left_child if right_child < len(heap) and heap[right_child] < heap[smallest]: smallest = right_child if smallest != index: heap[index], heap[smallest] = heap[smallest], heap[index] index = smallest else: break heap = [] values = [13, 16, 31, 41, 51, 100] for value in values: insert_min_heap(heap, value) print('Initial heap:', heap) delete_min_heap(heap, 13) print('Heap after deleting 13:', heap)> C# using System; using System.Collections.Generic; class MinHeap { private List tas = nouvelle liste (); public void Insert (valeur int) { tas.Add (valeur); int index = tas.Count - 1; while (index> 0 && tas[(index - 1) / 2]> tas[index]) { Swap(index, (index - 1) / 2); indice = (indice - 1) / 2 ; } } public void Supprimer (valeur int) { int index = tas.IndexOf (valeur); if (index == -1) {return; } tas[index] = tas[heap.Count - 1]; tas.RemoveAt(heap.Count - 1); while (true) { int leftChild = 2 * index + 1; int rightChild = 2 * index + 2; int le plus petit = indice ; si (enfant gauche< heap.Count && heap[leftChild] < heap[smallest]) { smallest = leftChild; } if (rightChild < heap.Count && heap[rightChild] < heap[smallest]) { smallest = rightChild; } if (smallest != index) { Swap(index, smallest); index = smallest; } else { break; } } } private void Swap(int i, int j) { int temp = heap[i]; heap[i] = heap[j]; heap[j] = temp; } public void Print() { for (int i = 0; i < heap.Count; i++) { Console.Write(heap[i] + ' '); } Console.WriteLine(); } } class Program { static void Main(string[] args) { MinHeap heap = new MinHeap(); int[] values = { 13, 16, 31, 41, 51, 100 }; for (int i = 0; i < values.Length; i++) { heap.Insert(values[i]); } Console.Write('Initial heap: '); heap.Print(); heap.Delete(13); Console.Write('Heap after deleting 13: '); heap.Print(); } }> Javascript function insertMinHeap(heap, value) { // Add the new element to the end of the heap heap.push(value); // Get the index of the last element let index = heap.length - 1; // Compare the new element with its parent and swap if necessary for (let flr = Math.floor((index - 1) / 2); index>0 && tas[flr]> tas[index]; flr = Math.floor((index - 1) / 2)) { [tas[index], tas[flr]] = [ tas[flr], tas[index], ]; // Remonte l'arborescence jusqu'au parent de l'élément actuel index = Math.floor((index - 1) / 2); } } function deleteMinHeap(heap, value) { // Trouver l'index de l'élément à supprimer let index = -1; pour (soit i = 0; i< heap.length; i++) { if (heap[i] == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last element heap[index] = heap[heap.length - 1]; // Remove the last element heap.pop(); // Heapify the tree starting from the element at the deleted index while (true) { let left_child = 2 * index + 1; let right_child = 2 * index + 2; let smallest = index; if (left_child < heap.length && heap[left_child] < heap[smallest]) { smallest = left_child; } if (right_child < heap.length && heap[right_child] < heap[smallest]) { smallest = right_child; } if (smallest != index) { [heap[index], heap[smallest]] = [heap[smallest], heap[index]]; index = smallest; } else { break; } } } // Main function to test the insertMinHeap and deleteMinHeap functions let heap = []; let values = [13, 16, 31, 41, 51, 100]; for (let i = 0; i < values.length; i++) { insertMinHeap(heap, values[i]); } console.log('Initial heap: ' + heap.join(' ')); deleteMinHeap(heap, 13); console.log('Heap after deleting 13: ' + heap.join(' '));> Sortir
Initial heap: 13 16 31 41 51 100 Heap after deleting 13: 16 41 31 100 51>
Complexité temporelle : O(log n) où n est le nombre d'éléments dans le tas
Espace auxiliaire : Sur)
3. Opération Peek sur la structure de données Min-Heap :
Pour accéder à l'élément minimum (c'est-à-dire la racine du tas), la valeur du nœud racine est renvoyée. La complexité temporelle du coup d'oeil dans un tas min est O(1).
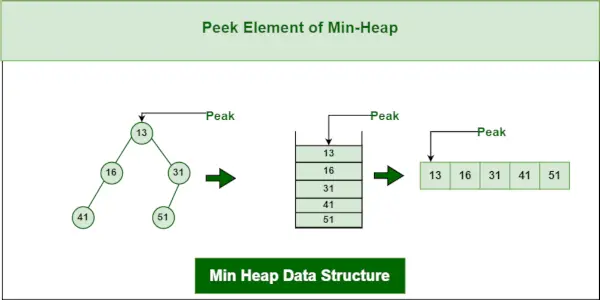
Structure de données minimale du tas
Implémentation de l'opération Peek dans Min-Heap :
C++ #include #include #include using namespace std; int main() { // Create a max heap with some elements using a // priority_queue priority_queue , plus grand > minTass ; minHeap.push(9); minHeap.push(8); minHeap.push(7); minHeap.push(6); minHeap.push(5); minHeap.push(4); minHeap.push(3); minHeap.push(2); minHeap.push(1); // Récupère l'élément de pointe (c'est-à-dire le plus grand élément) int PeakElement = minHeap.top(); // Imprimer le cout de l'élément de pointe<< 'Peak element: ' << peakElement << std::endl; return 0; }> Java import java.util.PriorityQueue; public class GFG { public static void main(String[] args) { // Create a max heap with some elements using a // PriorityQueue PriorityQueue minHeap = new PriorityQueue(); minHeap.add(9); minHeap.add(8); minHeap.add(7); minHeap.add(6); minHeap.add(5); minHeap.add(4); minHeap.add(3); minHeap.add(2); minHeap.add(1); // Récupère l'élément de pointe (c'est-à-dire le plus grand élément) int PeakElement = minHeap.peek(); // Imprimer l'élément de pointe System.out.println('Peak element: ' + PeakElement); } }> Python3 import heapq # Create a min heap with some elements using a list min_heap = [9, 8, 7, 6, 5, 4, 3, 2, 1] heapq.heapify(min_heap) # Get the peak element (i.e., the smallest element) peak_element = heapq.nsmallest(1, min_heap)[0] # Print the peak element print('Peak element:', peak_element)> C# using System; using System.Collections.Generic; public class GFG { public static void Main() { // Create a min heap with some elements using a // PriorityQueue var minHeap = new PriorityQueue (); minHeap.Enqueue(9); minHeap.Enqueue(8); minHeap.Enqueue(7); minHeap.Enqueue(6); minHeap.Enqueue(5); minHeap.Enqueue(4); minHeap.Enqueue(3); minHeap.Enqueue(2); minHeap.Enqueue(1); // Récupère l'élément de pointe (c'est-à-dire le plus petit élément) int PeakElement = minHeap.Peek(); // Imprimer l'élément de pointe Console.WriteLine('Peak element: ' + PeakElement); } }> Javascript const PriorityQueue = require('fast-priority-queue'); // Create a min heap with some elements using a PriorityQueue const minHeap = new PriorityQueue((a, b) =>un B); minHeap.add(9); minHeap.add(8); minHeap.add(7); minHeap.add(6); minHeap.add(5); minHeap.add(4); minHeap.add(3); minHeap.add(2); minHeap.add(1); // Récupère l'élément de pointe (c'est-à-dire le plus petit élément) const PeakElement = minHeap.peek(); // Imprimer l'élément de pointe console.log(`Peak element: ${peakElement}`);> Sortir
Peak element: 1>
Complexité temporelle : Dans un tas min implémenté à l'aide d'un tableau ou d'une liste, l'élément Peak est accessible en temps constant, O(1), car il est toujours situé à la racine du tas.
Dans un tas min implémenté à l'aide d'un arbre binaire, l'élément Peak est également accessible en temps O(1), car il est toujours situé à la racine de l'arbre.
Espace auxiliaire : Sur)
4. Opération Heapify sur la structure de données Min-Heap :
Une opération heapify peut être utilisée pour créer un tas min à partir d’un tableau non trié. Cela se fait en commençant par le dernier nœud non-feuille et en effectuant à plusieurs reprises l'opération de bulle vers le bas jusqu'à ce que tous les nœuds satisfassent à la propriété du tas.
Opération Heapify dans Min Heap
Implémentation de l'opération Heapify dans Min-Heap :
C++ #include #include using namespace std; void minHeapify(vector &arr, int i, int n) { int le plus petit = i; int l = 2*i + 1; int r = 2*i + 2; si (l< n && arr[l] < arr[smallest]) smallest = l; if (r < n && arr[r] < arr[smallest]) smallest = r; if (smallest != i) { swap(arr[i], arr[smallest]); minHeapify(arr, smallest, n); } } int main() { vector arr = {10, 5, 15, 2, 20, 30} ; cout<< 'Original array: '; for (int i = 0; i < arr.size(); i++) cout << arr[i] << ' '; // Perform heapify operation on min-heap for (int i = arr.size()/2 - 1; i>= 0 ; je--) minHeapify(arr, je, arr.size()); cout<< '
Min-Heap after heapify operation: '; for (int i = 0; i < arr.size(); i++) cout << arr[i] << ' '; return 0; }>
Java // Java code of Heapify operation in Min-Heap import java.util.Arrays; import java.util.List; public class Main { // Function to maintain the min-heap property of the heap rooted at index 'i' public static void minHeapify(List arr, int i, int n) { // Supposons que la racine soit le plus petit élément initialement int smallest = i; // Calcule les indices des enfants gauche et droit du nœud actuel int l = 2 * i + 1; int r = 2 * je + 2; // Comparez l'enfant de gauche avec le plus petit if (l< n && arr.get(l) < arr.get(smallest)) smallest = l; // Compare the right child with the current smallest if (r < n && arr.get(r) < arr.get(smallest)) smallest = r; // If the current node is not the smallest, swap it with the smallest child if (smallest != i) { int temp = arr.get(i); arr.set(i, arr.get(smallest)); arr.set(smallest, temp); // Recursively heapify the subtree rooted at the smallest child minHeapify(arr, smallest, n); } } public static void main(String[] args) { // Create a list representing the array List arr = Arrays.asList(10, 5, 15, 2, 20, 30); System.out.print('Tableau original : '); // Imprime le tableau d'origine pour (int i = 0; i< arr.size(); i++) System.out.print(arr.get(i) + ' '); // Perform heapify operation on the min-heap // Start from the last non-leaf node and go up to the root of the tree for (int i = arr.size() / 2 - 1; i>= 0 ; i--) minHeapify(arr, i, arr.size()); System.out.print('
Min-Heap après l'opération heapify : '); // Imprime le tas min après l'opération heapify pour (int i = 0; i< arr.size(); i++) System.out.print(arr.get(i) + ' '); } }> Python def minHeapify(arr, i, n): smallest = i left = 2 * i + 1 right = 2 * i + 2 if left < n and arr[left] < arr[smallest]: smallest = left if right < n and arr[right] < arr[smallest]: smallest = right if smallest != i: arr[i], arr[smallest] = arr[smallest], arr[i] minHeapify(arr, smallest, n) if __name__ == '__main__': arr = [10, 5, 15, 2, 20, 30] print('Original array:', arr) # Perform heapify operation on a min-heap for i in range(len(arr) // 2 - 1, -1, -1): minHeapify(arr, i, len(arr)) print('Min-Heap after heapify operation:', arr)> C# using System; using System.Collections.Generic; class GFG { // Function to perform the minHeapify operation on a min-heap. static void MinHeapify(List arr, int je, int n) { int le plus petit = je; int gauche = 2 * i + 1 ; int droite = 2 * i + 2 ; // Comparez l'enfant de gauche avec le plus petit nœud actuel. si (à gauche< n && arr[left] < arr[smallest]) smallest = left; // Compare the right child with the current smallest node. if (right < n && arr[right] < arr[smallest]) smallest = right; // If the current node is not the smallest // swap it with the smallest child. if (smallest != i) { int temp = arr[i]; arr[i] = arr[smallest]; arr[smallest] = temp; // Recursively call minHeapify on the affected subtree. MinHeapify(arr, smallest, n); } } static void Main(string[] args) { List arr = nouvelle liste { 10, 5, 15, 2, 20, 30 } ; Console.Write('Tableau d'origine : '); foreach (int num dans arr) Console.Write(num + ' '); // Effectue une opération heapify sur le min-heap. pour (int i = arr.Count / 2 - 1; i>= 0; i--) MinHeapify(arr, i, arr.Count); Console.Write('
Min-Heap après l'opération heapify : '); foreach (int num dans arr) Console.Write(num + ' '); } }> Javascript // Define a function to perform min-heapify operation on an array function minHeapify(arr, i, n) { let smallest = i; let l = 2 * i + 1; let r = 2 * i + 2; // Check if left child is smaller than the current smallest element if (l < n && arr[l] < arr[smallest]) smallest = l; // Check if right child is smaller than the current smallest element if (r < n && arr[r] < arr[smallest]) smallest = r; // If the smallest element is not the current element, swap them if (smallest !== i) { [arr[i], arr[smallest]] = [arr[smallest], arr[i]]; minHeapify(arr, smallest, n); } } // Main function function main() { const arr = [10, 5, 15, 2, 20, 30]; // Print the original array console.log('Original array: ' + arr.join(' ')); // Perform heapify operation on the min-heap for (let i = Math.floor(arr.length / 2) - 1; i>= 0 ; i--) minHeapify(arr, i, arr.length); // Imprimer le min-heap après l'opération heapify console.log('Min-Heap après l'opération heapify : ' + arr.join(' ')); } // Appelez la fonction main pour démarrer le processus main();> Sortir
Original array: 10 5 15 2 20 30 Min-Heap after heapify operation: 2 5 15 10 20 30>
La complexité temporelle de heapify dans un min-heap est O(n).
5. Opération de recherche sur la structure de données Min-Heap :
Pour rechercher un élément dans le tas min, une recherche linéaire peut être effectuée sur le tableau qui représente le tas. Cependant, la complexité temporelle d’une recherche linéaire est O(n), ce qui n’est pas efficace. Par conséquent, la recherche n’est pas une opération couramment utilisée dans un tas min.
Voici un exemple de code qui montre comment rechercher un élément dans un tas min en utilisant std :: trouver () :
C++ #include using namespace std; int main() { priority_queue , plus grand > min_tas ; // exemple de tas max min_heap.push(10); min_heap.push(9); min_heap.push(8); min_heap.push(6); min_heap.push(4); élément int = 6 ; // élément à rechercher bool trouvé = false; // Copiez le tas min dans une file d'attente temporaire et recherchez // l'élément std::priority_queue , plus grand > temp = min_heap; while (!temp.empty()) { if (temp.top() == element) { found = true; casser; } temp.pop(); } si (trouvé) { std :: cout<< 'Element found in the min heap.' << std::endl; } else { std::cout << 'Element not found in the min heap.' << std::endl; } return 0; }> Java import java.util.PriorityQueue; public class GFG { public static void main(String[] args) { PriorityQueue min_heap = new PriorityQueue(); min_heap.add( 3); // insère des éléments dans la file d'attente prioritaire min_heap.offer(1); min_heap.offer(4); min_heap.offer(1); min_heap.offer(6); élément int = 6 ; // élément à rechercher booléen trouvé = false; // Copiez le tas min dans une file d'attente temporaire et recherchez // l'élément PriorityQueue temp = new PriorityQueue (min_heap); while (!temp.isEmpty()) { if (temp.poll() == element) { found = true; casser; } } if (found) { System.out.println( 'Élément trouvé dans le tas min.'); } else { System.out.println( 'Élément introuvable dans le tas min.'); } } }> Python3 import heapq min_heap = [1, 2, 3, 5, 6, 7, 8, 10] # example min heap heapq.heapify(min_heap) element = 6 # element to search for found = False # Copy the min heap to a temporary list and search for the element temp = list(min_heap) while temp: if heapq.heappop(temp) == element: found = True break if found: print('Element found in the min heap.') else: print('Element not found in the min heap.')> C# using System; using System.Collections.Generic; public class GFG { public static void Main() { var minHeap = new PriorityQueue (); // exemple de tas min minHeap.Enqueue(4); minHeap.Enqueue(6); minHeap.Enqueue(8); minHeap.Enqueue(9); minHeap.Enqueue(10); élément int = 6 ; // élément à rechercher bool trouvé = false; // Copiez le tas min dans une file d'attente temporaire et recherchez // l'élément var temp = new PriorityQueue (minTas); while (temp.Count> 0) { if (temp.Peek() == element) { found = true ; casser; } temp.Dequeue(); } if (found) { Console.WriteLine( 'Élément trouvé dans le tas min.'); } else { Console.WriteLine( 'Élément introuvable dans le tas min.'); } } }> Javascript // Example min heap let minHeap = new PriorityQueue(); minHeap.enqueue(4); minHeap.enqueue(6); minHeap.enqueue(8); minHeap.enqueue(9); minHeap.enqueue(10); let element = 6; // Element to search for let found = false; // Copy the min heap to a temporary queue and search for the element let temp = new PriorityQueue(minHeap); while (temp.size()>0) { if (temp.peek() == element) { found = true ; casser; } temp.dequeue(); } if (found) { console.log('Élément trouvé dans le tas min.'); } else { console.log('Élément introuvable dans le tas min.'); }> Sortir
Element found in the min heap.>
Analyse de complexité :
Le complexité temporelle de ce programme est O (n journal n) , où n est le nombre d'éléments dans la file d'attente prioritaire.
L'opération d'insertion a une complexité temporelle de O (log n) dans le pire des cas, car la propriété du tas doit être conservée. L'opération de recherche consiste à copier la file d'attente prioritaire dans une file d'attente temporaire, puis à parcourir la file d'attente temporaire, ce qui prend O (n journal n) temps dans le pire des cas, car chaque élément doit être copié et retiré de la file d'attente, et la file d'attente prioritaire doit être reconstruite pour chaque opération.
Le complexité de l'espace du programme est Sur) parce qu'il stocke n éléments dans la file d'attente prioritaire et crée une file d'attente temporaire avec n éléments.
Applications de la structure de données Min-Heap :
- Tri en tas : Le tas min est utilisé comme composant clé dans l'algorithme de tri par tas qui est un algorithme de tri efficace avec une complexité temporelle de O (nlogn).
- File d'attente de priorité: Une file d'attente prioritaire peut être implémentée en utilisant une structure de données min tas où l'élément avec la valeur minimale est toujours à la racine.
- L'algorithme de Dijkstra : Dans l'algorithme de Dijkstra, un tas min est utilisé pour stocker les sommets du graphe avec la distance minimale du sommet de départ. Le sommet avec la distance minimale est toujours à la racine du tas.
- Codage de Huffman : Dans le codage de Huffman, un tas min est utilisé pour implémenter une file d'attente prioritaire afin de créer un code de préfixe optimal pour un ensemble de caractères donné.
- Fusionner K tableaux triés : Étant donné K tableaux triés, nous pouvons les fusionner efficacement en un seul tableau trié en utilisant une structure de données min tas.
Avantages de la structure de données Min-Heap :
- Insertion et suppression efficaces : Min tas permet une insertion et une suppression rapides d'éléments avec une complexité temporelle de O (log n), où n est le nombre d'éléments dans le tas.
- Récupération efficace de l'élément minimum : L'élément minimum dans un tas min est toujours à la racine du tas, qui peut être récupéré en un temps O(1).
- Efficacité de l'espace : Le tas min est une structure de données compacte qui peut être implémentée à l'aide d'un tableau ou d'un arbre binaire, ce qui la rend efficace en termes d'espace.
- Tri: Le tas min peut être utilisé pour implémenter un algorithme de tri efficace tel que le tri par tas avec une complexité temporelle de O (n log n).
- File d'attente de priorité: Le tas min peut être utilisé pour implémenter une file d'attente prioritaire, dans laquelle l'élément avec la priorité minimale peut être récupéré efficacement en un temps O(1).
- Polyvalence: Min Heap a plusieurs applications en informatique, notamment les algorithmes graphiques, la compression de données et les systèmes de bases de données.
Dans l’ensemble, le tas min est une structure de données utile et polyvalente qui offre des opérations efficaces, une efficacité spatiale et a plusieurs applications en informatique.