Centre d'un triangle est le point d'intersection des trois bissectrices d'un triangle. Le centre est un point important dans un triangle où les lignes coupant les angles en deux se rejoignent. Ce point est également le centre d’un cercle appelé Incircle qui s’intègre parfaitement à l’intérieur du triangle et touche les trois côtés de la même manière. Cet article couvre divers concepts du centre du triangle, tels que la raison pour laquelle ce point est important, comment le trouver à l'aide d'une boussole ou de chiffres et les propriétés du centre du cercle.

Table des matières

• Qu’est-ce que l’incentre d’un triangle ?
• Propriétés d'un incentre d'un triangle
• Incentre d'une formule triangulaire
• Comment trouver l'incentre d'un triangle
• Centroïde, Circoncentre, Incentre, Orthocentre

Qu’est-ce que l’incentre d’un triangle ?

Le centre d'un triangle, comme son nom l'indique, est le point central du triangle. Ce point que nous appelons incentre se forme à la jonction où se rencontrent toutes les lignes qui coupent en deux les angles intérieurs. La distance du point aux trois côtés du triangle est la même. Le cercle inscrit du triangle correspond également à un cercle parfait à l’intérieur du triangle et ce cercle est appelé le cercle inscrit du triangle.

Définition incentrique

Le centre d'un triangle est le point à l'intérieur du triangle où se rejoignent les trois lignes qui coupent ses angles intérieurs en deux. Ce point est à la même distance des trois côtés du triangle, ce qui en fait le milieu du triangle. C’est également le centre du plus grand cercle pouvant s’insérer parfaitement à l’intérieur du triangle, que nous appelons le cercle inscrit. Pour symboliser l'incentre, nous utilisons généralement la lettre I,

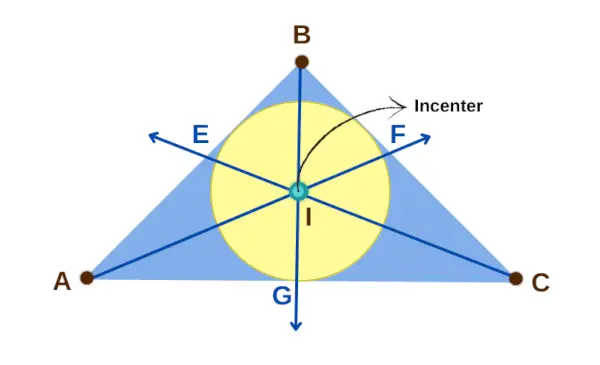
Centre d'un triangle

Propriétés d'un incentre d'un triangle

Certaines propriétés importantes du centre du triangle sont données ci-dessous :

Propriété 1 : Si je est le centre d'un triangle ABC, alors trois paires de segments de droite sont de même longueur : AE et AG, CG et CF, et BF et BE. Cela signifie que AE = AG, CG = CF et BF = BE.

Propriété 2 : L'incentre je a également une relation particulière avec les angles du triangle. Cela fait que les angles ∠BAI et ∠CAI sont égaux, ∠BCI et ∠ACI sont égaux et ∠ABI et ∠CBI sont égaux. Cela suit le théorème de la bissectrice de l’angle.

Propriété 3 : L'incentre je est le centre d'un cercle qui touche les trois côtés du triangle, et les distances de je les côtés du triangle (EI, FI, GI) sont tous identiques. Ces distances sont appelées rayons intérieurs, ou rayon du cercle inscrit.

Propriété 4 : Vous pouvez calculer l'aire du triangle en utilisant le(s) demi-périmètre(s) et le rayon intérieur (r). La formule est A = sr, où A est l'aire, s est le demi-périmètre (s = (a + b + c)/2, où a, b et c sont les longueurs des côtés du triangle) et r est le dans le rayon.

Propriété 5 : Le centre d'un triangle reste toujours à l'intérieur du triangle. Contrairement à l'orthocentre, qui peut se trouver à l'extérieur du triangle dans certains cas, l'incentre est toujours contenu dans les limites du triangle.

Incentre d'une formule triangulaire

La formule pour trouver l'incentre de la formule à 3 coordonnées (x₁, et₁), (X₂, et₂), et (x₃, et₃) est:

{(hache ₁ + boîte ₂ + CX ₃ )/(a + b + c), (est ₁ + par ₂ +c ₃ )/(une + b + c)}

En termes simples, pour obtenir l'incenter, vous :

• Multipliez la coordonnée x du point A par la longueur du côté a, la coordonnée x du point B par la longueur du côté b et la coordonnée x du point C par la longueur du côté c. Ensuite, additionnez-les ensemble.
• Divisez le résultat par la somme des longueurs des côtés a, b et c.
• Répétez le même processus pour les coordonnées y, mais en utilisant les longueurs de côté a, b et c.

Incentre d'une formule d'angle de triangle

La formule pour trouver le centre d’un angle d’un triangle est la suivante :

générer un nombre aléatoire en Java

Soit, dans un triangle D, F et G, les points où les bissectrices des angles A, B et C respectivement rencontrent les côtés BC, AC et AB.

L'angle ∠AIB (où I est le centre du triangle) peut être calculé à l'aide de la formule :

∠AIB = 180° – (la moitié de la somme des angles A et B)

OU

∠AIB = 180° – (∠A + ∠B)/2

Comment trouver l'incentre d'un triangle

Il existe deux méthodes pour trouver le centre d’un triangle. En construction, nous localisons l’incentre en traçant les bissectrices du triangle. En géométrie de coordonnées, nous employons une formule pour déterminer l'incentrage.

Utilisation de la géométrie des coordonnées : Trouvez le centre du triangle avec les coordonnées données comme : A(2, 2), B(6, 2) et C(4, 5)

D'après les informations données

• (X₁, et₁) = (2, 2)
• (X₂, et₂) = (6, 2)
• (X₃, et₃) = (4, 5)

On sait que le centre d'un triangle est :

je(x, y) = {(hache ₁ + boîte ₂ + CX ₃ )/(a + b + c), (est ₁ + par ₂ +c ₃ )/(une + b + c)}

Pour le côté a : La distance entre les points B et C = √((6 – 4)²+ (2 – 5)²) = √8

Pour le côté b : La distance entre les points A et C = √((2 – 4)²+ (2 – 5)²) = √13

Pour le côté c : La distance entre les points A et B = √((6 – 2)²+ (2 – 2)²) = 4

En mettant les valeurs de a, b, c dans la formule d'incentre, on obtient :

je(x, y) = {(8×2 + 13×5 + 4×4)/(8 + 13 +4), (8×2 + 13×2 + 4×5)/(8 + 13 +4 )}

⇒ Je(x, y) = (16 + 78 + 16)/(25), (16 + 26 + 20)/(25)

⇒ Je(x, y) = (110/25, 62/25) = (22/5,62/25)

∴ Le centre du triangle ABC de coordonnées est (22/5,62/25)

Comment construire l'incentre d'un triangle ?

Pour construire le centre d'un triangle, il faudra utiliser une boussole. À l'aide d'une boussole, suivez les étapes ci-dessous :

Étape 1: Placez une extrémité de la boussole sur un sommet du triangle et l'autre extrémité touche un côté.

Étape 2: Utilisez la boussole pour tracer deux arcs sur deux côtés du triangle.

Étape 3: Avec la même distance sur la boussole, faites deux arcs à l'intérieur du triangle. Ces arcs doivent se croiser là où ils touchent les côtés.

Étape 4: Tracez une ligne depuis le sommet du triangle jusqu’à l’endroit où les deux arcs intérieurs se croisent.

Étape 5 : Répétez les mêmes étapes depuis l’autre sommet du triangle.

Étape 6 : L’endroit où les deux lignes se rencontrent ou se croisent se trouve au centre du triangle.

Incentre du triangle à angle droit

L'incentre si un Triangle rectangle est le point où se rencontrent toutes les bissectrices d’un triangle rectangle. Si les côtés d'un triangle rectangle mesurent a, b et c, alors le rayon du cercle inscrit « r » est donné par r = (ab)/(a + b + c). Le centre du triangle rectangle est illustré ci-dessous :

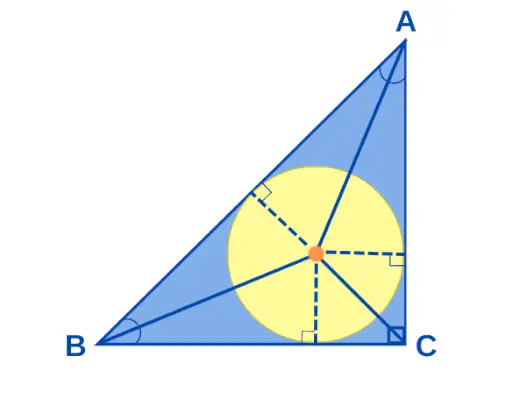
Incentre d'un triangle à angle droit

Centroïde, Circoncentre, Incentre, Orthocentre

Centroid, Circumcenter, Incenter et Orthocenter sont les quatre points importants liés à un traingle. Une comparaison entre Centroid, Circumcenter, Incenter et Orthocenter est présentée ci-dessous :

Vérifiez également

• Aire du Triangle
• Périmètre du Triangle
• Propriété de somme d'angle d'un triangle

Exemples d'incentrement d'un triangle

Exemple 1 : Calculez l'incentre du triangle ABC. AB = 8 cm, BC = 15 cm, CA = 17 cm.

Solution:

En utilisant la formule Incenter of Triangle = (aA + bB + cC)/(a + b + c)

où,

• une = 8
• b = 15
• c = 17

Et les angles sont,

• A = 30°
• B = 60°
• C = 90°

En mettant ces valeurs dans la formule pour obtenir,

⇒ {(8)(30) + (15)(60) + (17)(90)}/{8 + 15 + 17}

⇒ (240 + 900 + 1530)/40

⇒ 2670/40

⇒ 66,75

Exemple 2 : Jane a calculé la superficie d'un champ triangulaire à 120 mètres carrés. Le périmètre du terrain est de 36 mètres. Si un cercle est dessiné à l’intérieur du triangle de manière à toucher tous les côtés du triangle, aidez Jane à calculer le rayon intérieur du triangle.

Solution:

D'après les informations données,

Aire du triangle = 120 mètres carrés

Périmètre du triangle = 36 mètres

Nous savons que l'aire d'un triangle = r × s

s = demi-périmètre

s = p/2 = 36/2 = 18

UNE = r × s

r = A/s

r = 120/18

r = 6,67 mètres

Problèmes de pratique sur l'incentre d'un triangle

Problème 1 : Étant donné le triangle PQR avec les sommets P(1, 2), Q(4, 6) et R(7, 2), trouvez les coordonnées du centre.

Problème 2 : Construisez un triangle ABC avec ∠A = 45°, ∠B = 60° et ∠C = 75°. Utilisez la méthode de construction pour trouver l’incenter.

Problème 3 : Dans le triangle LMN, si ∠L = 75°, ∠M = 60° et ∠N = 45°, trouvez les coordonnées du centre.

Problème 4 : Construisez un triangle XYZ avec ∠X = 80°, ∠Y = 50° et ∠Z = 50°. Utilisez la méthode de construction pour trouver l’incenter.

Centre d'un triangle : FAQ

Qu’est-ce que l’incentre d’un triangle ?

Le centre d'un triangle est le point d'intersection des bissectrices des angles intérieurs. Il est à égale distance des trois côtés du triangle.

Quelle est la signification de l’incentre dans un triangle ?

L’incenter est significatif car il s’agit du centre du cercle inscrit du triangle, le plus grand cercle qui s’insère à l’intérieur du triangle. Il a la propriété d’être équidistant de tous côtés.

Incenter peut-il être en dehors du triangle ?

Non, l'incentre est toujours à l'intérieur du triangle. C'est le point de concurrence pour les bissectrices et, par définition, il doit se trouver dans les limites du triangle.

Comment Incenter est-il construit à l’aide d’une boussole et d’une règle ?

Pour construire l'incenter, utilisez un compas pour tracer des bissectrices de chaque sommet vers le côté opposé. L'incentre est le point d'intersection de ces bissectrices.

Qu’est-ce que la formule Incenter ?

La formule pour l'incentre d'un triangle peut s'écrire comme suit :

frac{(aA+bB+cC)}{a+b+c}

Quelles sont les propriétés de l’incentre d’un triangle ?

L'incenter a quelques propriétés clés. Il est équidistant des côtés du triangle, ce qui signifie que les distances entre les côtés sont égales. C’est également le point d’intersection des bissectrices des angles, divisant les angles en deux parties égales.

Comment l’Incentre est-il déterminé ?

Pour déterminer l'incentre, vous devez trouver l'endroit où les bissectrices se croisent. Cela peut être fait en utilisant la formule d'incentration ou en traçant les bissectrices de l'angle et en trouvant leur point d'intersection.

Quelle est la différence entre Incentre et Circoncentre ?

La principale différence entre l'incenter et le circumcenter réside dans leur orientation. Le centre concerne les bissectrices de l'angle et est le centre du cercle inscrit, tandis que le centre circonscrit concerne les bissectrices perpendiculaires et est le centre du cercle circonscrit.

L'Incentre et le Centroïde sont-ils identiques ?

Non, l'incenter et le centroïde sont différents. Le centre est l'endroit où les bissectrices se rencontrent, tandis que le centre de gravité est l'endroit où les médianes se croisent. Les médianes relient les sommets au milieu du côté opposé.

Incentre et Orthocentre sont-ils identiques ?

Non, l'incentre et l'orthocentre ne sont pas les mêmes. L'incentre est le point où l'angle se coupe en deux, tandis que l'orthocentre implique des altitudes – des lignes partant de chaque sommet perpendiculaires au côté opposé. Ce sont différents points dans un triangle.