ALGORITHME FLOYD WARSHALL

Le Algorithme de Floyd-Warshall , du nom de ses créateurs Robert Floyd et Stephen Warshall , est un algorithme fondamental en informatique et en théorie des graphes. Il est utilisé pour trouver les chemins les plus courts entre toutes les paires de nœuds dans un graphe pondéré. Cet algorithme est très efficace et peut gérer des graphiques avec les deux positif et n poids des bords négatifs , ce qui en fait un outil polyvalent pour résoudre un large éventail de problèmes de réseau et de connectivité.

Table des matières

Algorithme Floyd Warshall
Idée derrière l'algorithme de Floyd Warshall
Algorithme Floyd Warshall Algorithme
Pseudo-code de l'algorithme Floyd Warshall
Illustration de l'algorithme Floyd Warshall
Analyse de la complexité de l'algorithme Floyd Warshall
Pourquoi l'algorithme Floyd-Warshall est-il meilleur pour les graphiques denses et non pour les graphiques clairsemés ?
Questions d'entretien importantes liées à Floyd-Warshall
Applications réelles de l'algorithme Floyd-Warshall

Bannière-d'algorithme-Floyd-Warshall

Algorithme Floyd Warshall :

Le Algorithme Floyd Warshall est un algorithme de chemin le plus court composé de paires contrairement à Dijkstra et Bellman Ford qui sont des algorithmes de chemin le plus court à source unique. Cet algorithme fonctionne à la fois pour le dirigé et non orienté pondéré graphiques. Mais cela ne fonctionne pas pour les graphiques avec des cycles négatifs (où la somme des arêtes d'un cycle est négative). Ça suit Programmation dynamique approche pour vérifier tous les chemins possibles passant par chaque nœud possible afin de calculer la distance la plus courte entre chaque paire de nœuds.
mylivecricket.in

Idée derrière l'algorithme Floyd Warshall :

Supposons que nous ayons un graphique G[][] avec DANS sommets de 1 à N . Il nous faut maintenant évaluer un la matrice de chemin la plus courte[][] où s la plus courtePathMatrix[i][j] représente le chemin le plus court entre les sommets je et j .

Évidemment, le chemin le plus court entre je à j en aura k nombre de nœuds intermédiaires. L'idée derrière l'algorithme de Floyd Warshall est de traiter chaque sommet de 1 à N comme nœud intermédiaire un par un.

La figure suivante montre la propriété de sous-structure optimale ci-dessus dans l'algorithme de Floyd Warshall :

Algorithme de l'algorithme Floyd Warshall :

Initialisez la matrice de solution de la même manière que la matrice du graphique d'entrée dans un premier temps.
Mettez ensuite à jour la matrice de solution en considérant tous les sommets comme sommet intermédiaire.
L'idée est de sélectionner tous les sommets un par un et de mettre à jour tous les chemins les plus courts qui incluent le sommet sélectionné comme sommet intermédiaire dans le chemin le plus court.
Quand nous choisissons le numéro du sommet k comme sommet intermédiaire, nous avons déjà considéré les sommets {0, 1, 2, .. k-1} comme sommets intermédiaires.
Pour chaque paire (je, j) des sommets source et destination respectivement, il y a deux cas possibles.
- k n'est pas un sommet intermédiaire sur le chemin le plus court depuis je à j . Nous gardons la valeur de dist[i][j] tel quel.
- k est un sommet intermédiaire sur le chemin le plus court depuis je à j . Nous mettons à jour la valeur de dist[i][j] comme dist[i][k] + dist[k][j], si dist[i][j]> dist[i][k] + dist[k][j]

Pseudo-Code de l'algorithme Floyd Warshall :`>`

Pour k = 0 à n – 1
Pour i = 0 à n – 1
Pour j = 0 à n – 1
Distance[i, j] = min(Distance[i, j], Distance[i, k] + Distance[k, j])

où i = nœud source, j = nœud de destination, k = nœud intermédiaire

Illustration de l'algorithme Floyd Warshall :

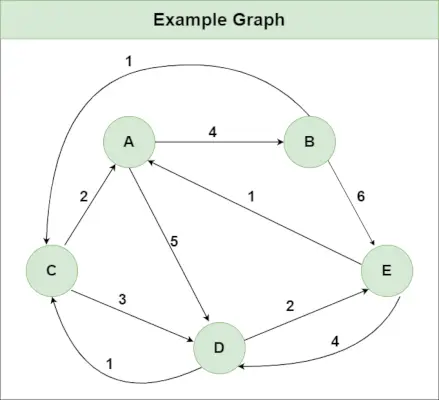
Supposons que nous ayons un graphique comme indiqué dans l'image :
classe abstraite Java

Étape 1 : Initialisez la matrice Distance[][] à l'aide du graphique d'entrée tel que Distance[i][j]= poids du bord de je à j , également Distance[i][j] = Infinity s'il n'y a pas d'arête depuis je à j.

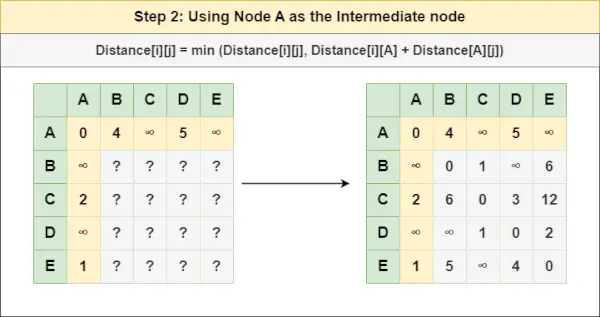
Étape 2 : Traiter le nœud UN comme nœud intermédiaire et calculez la Distance[][] pour chaque paire de nœuds {i,j} en utilisant la formule :

= Distance[i][j] = minimum (Distance[i][j], (Distance de i à UN ) + (Distance de UN à j ))
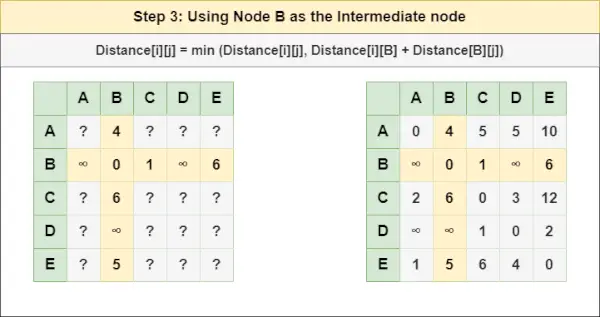
= Distance[i][j] = minimum (Distance[i][j], Distance[i][ UN ] + Distance[ UN ][j])

Étape 3 : Traiter le nœud B comme nœud intermédiaire et calculez la Distance[][] pour chaque paire de nœuds {i,j} en utilisant la formule :

= Distance[i][j] = minimum (Distance[i][j], (Distance de i à B ) + (Distance de B à j ))
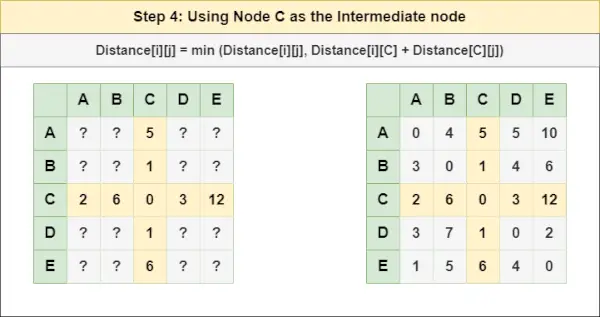
= Distance[i][j] = minimum (Distance[i][j], Distance[i][ B ] + Distance[ B ][j])

Étape 4 : Traiter le nœud C comme nœud intermédiaire et calculez la Distance[][] pour chaque paire de nœuds {i,j} en utilisant la formule :

= Distance[i][j] = minimum (Distance[i][j], (Distance de i à C ) + (Distance de C à j ))
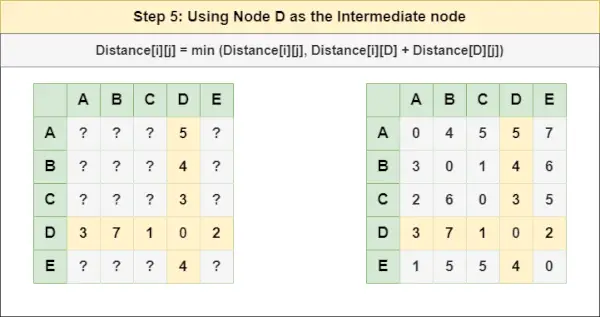
= Distance[i][j] = minimum (Distance[i][j], Distance[i][ C ] + Distance[ C ][j])

Étape 5 : Traiter le nœud D comme nœud intermédiaire et calculez la Distance[][] pour chaque paire de nœuds {i,j} en utilisant la formule :
mylivecricket pour le cricket en direct

= Distance[i][j] = minimum (Distance[i][j], (Distance de i à D ) + (Distance de D à j ))
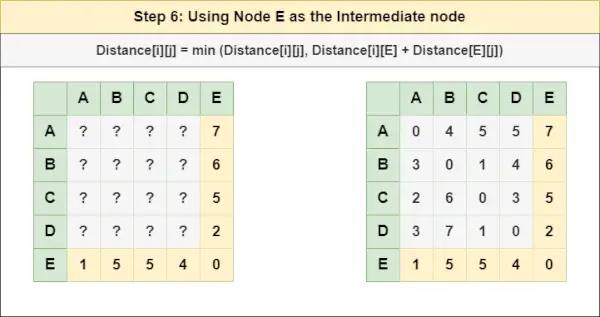
= Distance[i][j] = minimum (Distance[i][j], Distance[i][ D ] + Distance[ D ][j])

Étape 6 : Traiter le nœud ET comme nœud intermédiaire et calculez la Distance[][] pour chaque paire de nœuds {i,j} en utilisant la formule :

= Distance[i][j] = minimum (Distance[i][j], (Distance de i à ET ) + (Distance de ET à j ))
= Distance[i][j] = minimum (Distance[i][j], Distance[i][ ET ] + Distance[ ET ][j])

Étape 7 : Puisque tous les nœuds ont été traités comme un nœud intermédiaire, nous pouvons maintenant renvoyer la matrice Distance[][] mise à jour comme matrice de réponse.

Pratique recommandée Essayez-le !

Vous trouverez ci-dessous la mise en œuvre de l’approche ci-dessus :

C++

 // C++ Program for Floyd Warshall Algorithm #include  using namespace std; // Number of vertices in the graph #define V 4 /* Define Infinite as a large enough value.This value will be used for vertices not connected to each other */ #define INF 99999 // A function to print the solution matrix void printSolution(int dist[][V]); // Solves the all-pairs shortest path // problem using Floyd Warshall algorithm void floydWarshall(int dist[][V]) {  int i, j, k;  /* Add all vertices one by one to  the set of intermediate vertices.  --->Avant le début d'une itération, nous avons les distances les plus courtes entre toutes les paires de sommets telles que les distances les plus courtes ne considèrent que les sommets de l'ensemble {0, 1, 2, .. k-1} comme sommets intermédiaires.  ----> Après la fin d'une itération, le sommet no. k est ajouté à l'ensemble des sommets intermédiaires et l'ensemble devient {0, 1, 2, .. k} */ pour (k = 0; k< V; k++) {  // Pick all vertices as source one by one  for (i = 0; i < V; i++) {  // Pick all vertices as destination for the  // above picked source  for (j = 0; j < V; j++) {  // If vertex k is on the shortest path from  // i to j, then update the value of  // dist[i][j]  if (dist[i][j]>(dist[i][k] + dist[k][j]) && (dist[k][j] != INF && dist[i][k] != INF)) dist[i][j] = dist[i][k] + dist[k][j];  } } } // Imprimer la matrice de distance la plus courte printSolution(dist); } /* Une fonction utilitaire pour imprimer la solution */ void printSolution(int dist[][V]) { cout<< 'The following matrix shows the shortest '  'distances'  ' between every pair of vertices 
';  for (int i = 0; i < V; i++) {  for (int j = 0; j < V; j++) {  if (dist[i][j] == INF)  cout << 'INF'  << ' ';  else  cout << dist[i][j] << ' ';  }  cout << endl;  } } // Driver's code int main() {  /* Let us create the following weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int graph[V][V] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, { INF, INF, INF, 0 } } ;  // Appel de fonction floydWarshall(graph);  renvoie 0 ; } // Ce code est contribué par Mythri J L>

 // C Program for Floyd Warshall Algorithm #include  // Number of vertices in the graph #define V 4 /* Define Infinite as a large enough  value. This value will be used  for vertices not connected to each other */ #define INF 99999 // A function to print the solution matrix void printSolution(int dist[][V]); // Solves the all-pairs shortest path // problem using Floyd Warshall algorithm void floydWarshall(int dist[][V]) {  int i, j, k;  /* Add all vertices one by one to  the set of intermediate vertices.  --->Avant le début d'une itération, nous avons les distances les plus courtes entre toutes les paires de sommets telles que les distances les plus courtes ne considèrent que les sommets de l'ensemble {0, 1, 2, .. k-1} comme sommets intermédiaires.  ----> Après la fin d'une itération, le sommet no. k est ajouté à l'ensemble des sommets intermédiaires et l'ensemble devient {0, 1, 2, .. k} */ pour (k = 0; k< V; k++) {  // Pick all vertices as source one by one  for (i = 0; i < V; i++) {  // Pick all vertices as destination for the  // above picked source  for (j = 0; j < V; j++) {  // If vertex k is on the shortest path from  // i to j, then update the value of  // dist[i][j]  if (dist[i][k] + dist[k][j] < dist[i][j])  dist[i][j] = dist[i][k] + dist[k][j];  }  }  }  // Print the shortest distance matrix  printSolution(dist); } /* A utility function to print solution */ void printSolution(int dist[][V]) {  printf(  'The following matrix shows the shortest distances'  ' between every pair of vertices 
');  for (int i = 0; i < V; i++) {  for (int j = 0; j < V; j++) {  if (dist[i][j] == INF)  printf('%7s', 'INF');  else  printf('%7d', dist[i][j]);  }  printf('
');  } } // driver's code int main() {  /* Let us create the following weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int graph[V][V] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, { INF, INF, INF, 0 } } ;  // Appel de fonction floydWarshall(graph);  renvoie 0 ; }>

Java

 // Java program for Floyd Warshall All Pairs Shortest // Path algorithm. import java.io.*; import java.lang.*; import java.util.*; class AllPairShortestPath {  final static int INF = 99999, V = 4;  void floydWarshall(int dist[][])  {  int i, j, k;  /* Add all vertices one by one  to the set of intermediate  vertices.  --->Avant le début d'une itération, nous avons les distances les plus courtes entre toutes les paires de sommets telles que les distances les plus courtes ne considèrent que les sommets de l'ensemble {0, 1, 2, .. k-1} comme sommets intermédiaires.  ----> Après la fin d'une itération, le sommet no. k est ajouté à l'ensemble des sommets intermédiaires et l'ensemble devient {0, 1, 2, .. k} */ pour (k = 0; k< V; k++) {  // Pick all vertices as source one by one  for (i = 0; i < V; i++) {  // Pick all vertices as destination for the  // above picked source  for (j = 0; j < V; j++) {  // If vertex k is on the shortest path  // from i to j, then update the value of  // dist[i][j]  if (dist[i][k] + dist[k][j]  < dist[i][j])  dist[i][j]  = dist[i][k] + dist[k][j];  }  }  }  // Print the shortest distance matrix  printSolution(dist);  }  void printSolution(int dist[][])  {  System.out.println(  'The following matrix shows the shortest '  + 'distances between every pair of vertices');  for (int i = 0; i < V; ++i) {  for (int j = 0; j < V; ++j) {  if (dist[i][j] == INF)  System.out.print('INF ');  else  System.out.print(dist[i][j] + ' ');  }  System.out.println();  }  }  // Driver's code  public static void main(String[] args)  {  /* Let us create the following weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int graph[][] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, { INF, INF, INF, 0 } } ;  AllPairShortestPath a = new AllPairShortestPath();  // Appel de fonction a.floydWarshall(graph);  } } // Contribution de Aakash Hasija>

Python3

 # Python3 Program for Floyd Warshall Algorithm # Number of vertices in the graph V = 4 # Define infinity as the large # enough value. This value will be # used for vertices not connected to each other INF = 99999 # Solves all pair shortest path # via Floyd Warshall Algorithm def floydWarshall(graph):  ''' dist[][] will be the output   matrix that will finally  have the shortest distances   between every pair of vertices '''  ''' initializing the solution matrix   same as input graph matrix  OR we can say that the initial   values of shortest distances  are based on shortest paths considering no   intermediate vertices ''' dist = list(map(lambda i: list(map(lambda j: j, i)), graph))  ''' Add all vertices one by one   to the set of intermediate  vertices.  --->Avant le début d'une itération, nous avons les distances les plus courtes entre toutes les paires de sommets telles que les distances les plus courtes ne considèrent que les sommets de l'ensemble {0, 1, 2, .. k-1} comme sommets intermédiaires.  ----> Après la fin d'une itération, le sommet no. k est ajouté à l'ensemble des sommets intermédiaires et l'ensemble devient {0, 1, 2, .. k} ''' pour k dans la plage (V) : # sélectionne tous les sommets comme source un par un pour i dans range(V): # Choisissez tous les sommets comme destination pour la # source choisie ci-dessus pour j dans range(V): # Si le sommet k est sur le chemin le plus court de # i à j, alors mettez à jour la valeur de dist[i][ j] dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j] ) printSolution(dist) # Une fonction utilitaire pour imprimer la solution def printSolution (dist) : print('La matrice suivante montre les distances les plus courtes entre chaque paire de sommets') pour i dans la plage(V) : pour j dans la plage(V) : if(dist[i][j] == INF): print('%7s' % ('INF'), end=' ') sinon : print('%7d	' % (dist[i][j]), end=' ') if j == V-1: print() # Code du pilote if __name__ == '__main__': ''' 10 (0)------ ->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 ''' graphique = [[0, 5, INF, 10], [INF, 0, 3, INF], [INF, INF, 0 , 1], [INF, INF, INF, 0] ] # Appel de fonction floydWarshall(graph) # Ce code est fourni par Mythri J L>

 // C# program for Floyd Warshall All // Pairs Shortest Path algorithm. using System; public class AllPairShortestPath {  readonly static int INF = 99999, V = 4;  void floydWarshall(int[, ] graph)  {  int[, ] dist = new int[V, V];  int i, j, k;  // Initialize the solution matrix  // same as input graph matrix  // Or we can say the initial  // values of shortest distances  // are based on shortest paths  // considering no intermediate  // vertex  for (i = 0; i < V; i++) {  for (j = 0; j < V; j++) {  dist[i, j] = graph[i, j];  }  }  /* Add all vertices one by one to  the set of intermediate vertices.  --->Avant le début d'une itération, nous avons les distances les plus courtes entre toutes les paires de sommets telles que les distances les plus courtes ne considèrent que les sommets de l'ensemble {0, 1, 2, .. k-1} comme sommets intermédiaires.  ---> Après la fin d'une itération, le sommet no. k est ajouté à l'ensemble des sommets intermédiaires et l'ensemble devient {0, 1, 2, .. k} */ pour (k = 0; k< V; k++) {  // Pick all vertices as source  // one by one  for (i = 0; i < V; i++) {  // Pick all vertices as destination  // for the above picked source  for (j = 0; j < V; j++) {  // If vertex k is on the shortest  // path from i to j, then update  // the value of dist[i][j]  if (dist[i, k] + dist[k, j]  < dist[i, j]) {  dist[i, j]  = dist[i, k] + dist[k, j];  }  }  }  }  // Print the shortest distance matrix  printSolution(dist);  }  void printSolution(int[, ] dist)  {  Console.WriteLine(  'Following matrix shows the shortest '  + 'distances between every pair of vertices');  for (int i = 0; i < V; ++i) {  for (int j = 0; j < V; ++j) {  if (dist[i, j] == INF) {  Console.Write('INF ');  }  else {  Console.Write(dist[i, j] + ' ');  }  }  Console.WriteLine();  }  }  // Driver's Code  public static void Main(string[] args)  {  /* Let us create the following  weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int[, ] graphique = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0 , 1 }, { INF, INF, INF, 0 } } ;  AllPairShortestPath a = new AllPairShortestPath();  // Appel de fonction a.floydWarshall(graph);  } } // Cet article est rédigé par // Abdul Mateen Mohammed>

Javascript

 // A JavaScript program for Floyd Warshall All  // Pairs Shortest Path algorithm.  var INF = 99999;  class AllPairShortestPath {  constructor() {  this.V = 4;  }  floydWarshall(graph) {  var dist = Array.from(Array(this.V), () =>nouveau tableau(this.V).fill(0));  var je, j, k;  // Initialise la matrice de solution // identique à la matrice du graphe d'entrée // Ou nous pouvons dire que les // valeurs initiales des distances les plus courtes // sont basées sur les chemins les plus courts // ne considérant aucun sommet intermédiaire // pour (i = 0; i< this.V; i++) {  for (j = 0; j < this.V; j++) {  dist[i][j] = graph[i][j];  }  }  /* Add all vertices one by one to  the set of intermediate vertices.  --->Avant le début d'une itération, nous avons les distances les plus courtes entre toutes les paires de sommets telles que les distances les plus courtes ne considèrent que les sommets de l'ensemble {0, 1, 2, .. k-1} comme sommets intermédiaires.  ---> Après la fin d'une itération, le sommet no. k est ajouté à l'ensemble des sommets intermédiaires et l'ensemble devient {0, 1, 2, .. k} */ pour (k = 0; k< this.V; k++) {  // Pick all vertices as source  // one by one  for (i = 0; i < this.V; i++) {  // Pick all vertices as destination  // for the above picked source  for (j = 0; j < this.V; j++) {  // If vertex k is on the shortest  // path from i to j, then update  // the value of dist[i][j]  if (dist[i][k] + dist[k][j] < dist[i][j]) {  dist[i][j] = dist[i][k] + dist[k][j];  }  }  }  }  // Print the shortest distance matrix  this.printSolution(dist);  }  printSolution(dist) {  document.write(  'Following matrix shows the shortest ' +  'distances between every pair of vertices '  );  for (var i = 0; i < this.V; ++i) {  for (var j = 0; j < this.V; ++j) {  if (dist[i][j] == INF) {  document.write(' INF ');  } else {  document.write('  ' + dist[i][j] + ' ');  }  }  document.write(' ');  }  }  }  // Driver Code  /* Let us create the following  weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ var graphique = [ [0, 5, INF, 10], [INF, 0, 3, INF], [INF, INF, 0, 1] , [INF, INF, INF, 0], ] ;  var a = new AllPairShortestPath();  // Imprimer la solution a.floydWarshall(graph);    // Ce code est contribué par rdtaank.>

PHP

  // PHP Program for Floyd Warshall Algorithm  // Solves the all-pairs shortest path problem // using Floyd Warshall algorithm  function floydWarshall ($graph, $V, $INF) { /* dist[][] will be the output matrix   that will finally have the shortest   distances between every pair of vertices */ $dist = array(array(0,0,0,0), array(0,0,0,0), array(0,0,0,0), array(0,0,0,0)); /* Initialize the solution matrix same   as input graph matrix. Or we can say the   initial values of shortest distances are   based on shortest paths considering no   intermediate vertex. */ for ($i = 0; $i < $V; $i++) for ($j = 0; $j < $V; $j++) $dist[$i][$j] = $graph[$i][$j]; /* Add all vertices one by one to the set   of intermediate vertices.   --->Avant le début d'une itération, nous avons les distances les plus courtes entre toutes les paires de sommets telles que les distances les plus courtes ne considèrent que les sommets de l'ensemble {0, 1, 2, .. k-1} comme sommets intermédiaires.   ----> Après la fin d'une itération, le sommet no. k est ajouté à l'ensemble des sommets intermédiaires et l'ensemble devient {0, 1, 2, .. k} */ pour ($k = 0; $k< $V; $k++) { // Pick all vertices as source one by one  for ($i = 0; $i < $V; $i++) { // Pick all vertices as destination  // for the above picked source  for ($j = 0; $j < $V; $j++) { // If vertex k is on the shortest path from  // i to j, then update the value of dist[i][j]  if ($dist[$i][$k] + $dist[$k][$j] < $dist[$i][$j]) $dist[$i][$j] = $dist[$i][$k] + $dist[$k][$j]; } } } // Print the shortest distance matrix  printSolution($dist, $V, $INF); } /* A utility function to print solution */ function printSolution($dist, $V, $INF) { echo 'The following matrix shows the ' . 'shortest distances between ' . 'every pair of vertices 
'; for ($i = 0; $i < $V; $i++) { for ($j = 0; $j < $V; $j++) { if ($dist[$i][$j] == $INF) echo 'INF ' ; else echo $dist[$i][$j], ' '; } echo '
'; } } // Drivers' Code // Number of vertices in the graph  $V = 4 ; /* Define Infinite as a large enough  value. This value will be used for vertices not connected to each other */ $INF = 99999 ; /* Let us create the following weighted graph   10  (0)------->(3) | /| 5 | |   | | 1 |/ |  (1)------->(2) 3 */ $graph = array(array(0, 5, $INF, 10), array($INF, 0, 3, $INF), array($ INF, $INF, 0, 1), tableau($INF, $INF, $INF, 0)); // Appel de fonction floydWarshall($graph, $V, $INF); // Ce code est contribué par Ryuga ?>>

Sortir

The following matrix shows the shortest distances between every pair of vertices 0 5 8 9 INF 0 3 4 INF INF 0 1 INF INF INF 0>

Analyse de la complexité de l'algorithme Floyd Warshall :

Complexité temporelle : O(V³), où V est le nombre de sommets dans le graphique et nous exécutons trois boucles imbriquées chacune de taille V
Espace auxiliaire : O(V²), pour créer une matrice 2D afin de stocker la distance la plus courte pour chaque paire de nœuds.

Note : Le programme ci-dessus imprime uniquement les distances les plus courtes. Nous pouvons également modifier la solution pour imprimer les chemins les plus courts en stockant les informations du prédécesseur dans une matrice 2D distincte.

chaîne json java

Pourquoi l'algorithme Floyd-Warshall est-il meilleur pour les graphiques denses et non pour les graphiques clairsemés ?

Graphique dense : Un graphe dans lequel le nombre d’arêtes est nettement supérieur au nombre de sommets.
Graphique clairsemé : Un graphe dans lequel le nombre d'arêtes est très faible.

Quel que soit le nombre d’arêtes du graphique, Algorithme Floyd Warshall fonctionne pour O(V³) fois, il est donc mieux adapté pour Graphiques denses . Dans le cas de graphes clairsemés, L'algorithme de Johnson est plus adapté.

Comment détecter un cycle négatif dans un graphique à l'aide de l'algorithme Floyd Warshall ?
En quoi l’algorithme de Floyd-Warshall est-il différent de l’algorithme de Dijkstra ?
En quoi l’algorithme de Floyd-Warshall est-il différent de l’algorithme de Bellman-Ford ?

Applications réelles de l'algorithme Floyd-Warshall :

Dans les réseaux informatiques, l'algorithme peut être utilisé pour trouver le chemin le plus court entre toutes les paires de nœuds d'un réseau. Ceci est appelé comme routage réseau .
Connectivité des vols Dans l'industrie aéronautique, pour trouver le chemin le plus court entre les aéroports.
SIG ( Systèmes d'information géographique ) les applications impliquent souvent l'analyse de données spatiales, telles que les réseaux routiers, pour trouver les chemins les plus courts entre les emplacements.
L'algorithme de Kleene qui est une généralisation de Floyd Warshall, peut être utilisé pour trouver une expression régulière pour un langage régulier.